Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the osculating parabola of a plane curve
ResourceFunction["OsculatingParabola"][c,{t,t0},u] gives the parametric equations with parameter u for the osculating parabola of a plane curve c defined with respect to the variable t at t=t0. |
Parametric equations for the osculating parabola of a semicubical parabola:
| In[1]:= |
![para = ResourceFunction["OsculatingParabola"][
Entity["PlaneCurve", "SemicubicalParabola"]["ParametricEquations"][
a][t], {t, t0}, u] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/b88/b88a7303-7570-43e2-978b-3eecbe0bbfea/3cf0a28aa689cb66.png)
|
| Out[1]= |
|
Plot the curve and its osculating parabola with the point of contact:
| In[2]:= |
![Show[ParametricPlot[
Evaluate[Entity["PlaneCurve", "SemicubicalParabola"][
"ParametricEquations"][a][t] /. a -> 1], {t, -1, 5/4}, PlotStyle -> Thick],
ParametricPlot[Evaluate[para /. {a -> 1, t0 -> 1}], {u, -5/2, 5/2}, PlotStyle -> Directive[Dashed, ColorData[97, 2]]],
Graphics[{Directive[ColorData[97, 4], AbsolutePointSize[4]], Point[Entity["PlaneCurve", "SemicubicalParabola"][
"ParametricEquations"][a][t0] /. {a -> 1, t0 -> 1}]}],
PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/b88/b88a7303-7570-43e2-978b-3eecbe0bbfea/6fbf920649424501.png)
|
| Out[2]= |
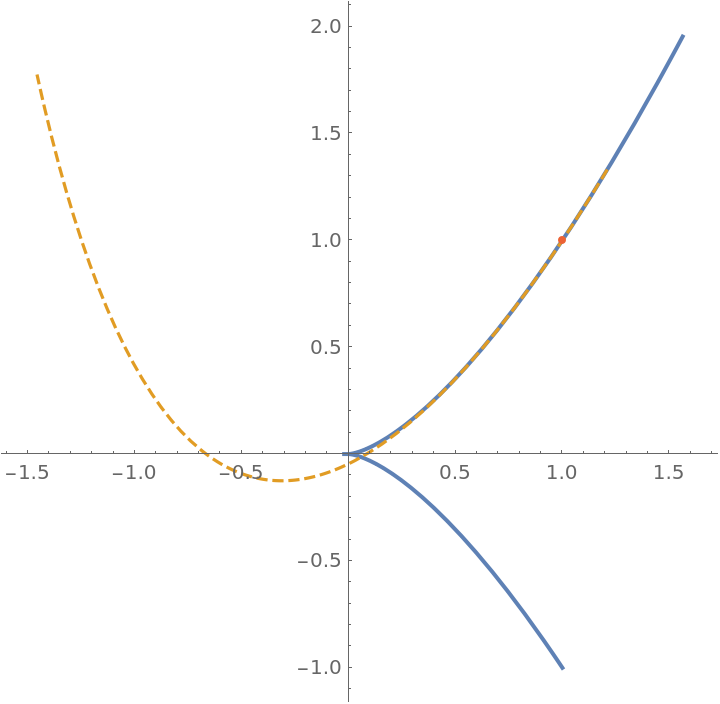
|
Plot a family of osculating parabolas for a cardioid:
| In[3]:= |
![With[{a = 1},
Show[Table[
ParametricPlot[
Evaluate[
ResourceFunction["OsculatingParabola"][
Entity["PlaneCurve", "Cardioid"]["ParametricEquations"][a][
t], {t, tmp}, u]], {u, -2, 2}, PlotStyle -> Directive[Thin, Red]], {tmp, \[Pi]/20, 2 \[Pi] - \[Pi]/20, \[Pi]/20}], PlotRange -> All]]](https://www.wolframcloud.com/obj/resourcesystem/images/b88/b88a7303-7570-43e2-978b-3eecbe0bbfea/4e8ee6b4b014f062.png)
|
| Out[3]= |
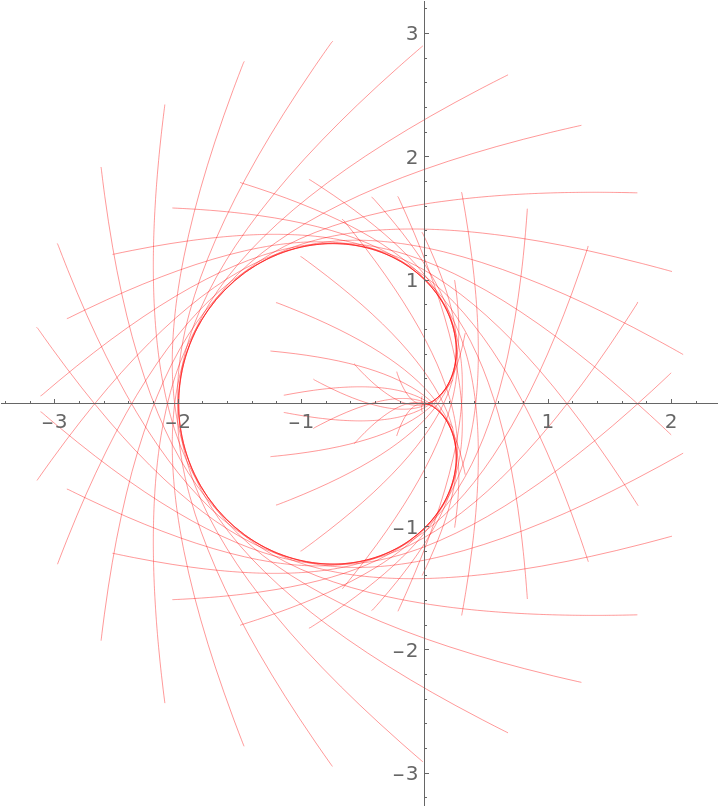
|
Generate the implicit Cartesian equation for the osculating parabola of an ellipse at a given point:
| In[4]:= |
![With[{a = Sqrt[2], b = 1, t0 = \[Pi]/4},
Eliminate[
Thread[{x, y} == Simplify[
ResourceFunction["OsculatingParabola"][
Entity["PlaneCurve", "Ellipse"]["ParametricEquations"][a, b][
t], {t, t0}, u]]], u]]](https://www.wolframcloud.com/obj/resourcesystem/images/b88/b88a7303-7570-43e2-978b-3eecbe0bbfea/56d581fca3e9fac0.png)
|
| Out[4]= |
|
Show the ellipse, the osculating parabola, and their point of contact:
| In[5]:= |
![ContourPlot[Evaluate[%], {x, -2, 2}, {y, -2, 2},
Epilog -> Evaluate[{Directive[AbsolutePointSize[5], ColorData[97, 3]], Point[Entity["PlaneCurve", "Ellipse"]["ParametricEquations"][Sqrt[
2], 1][t] /. t -> \[Pi]/4]}],
Prolog -> {Directive[FaceForm[], EdgeForm[ColorData[97, 4]]], Ellipsoid[{0, 0}, {Sqrt[2], 1}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b88/b88a7303-7570-43e2-978b-3eecbe0bbfea/501c367944f3f5ae.png)
|
| Out[5]= |
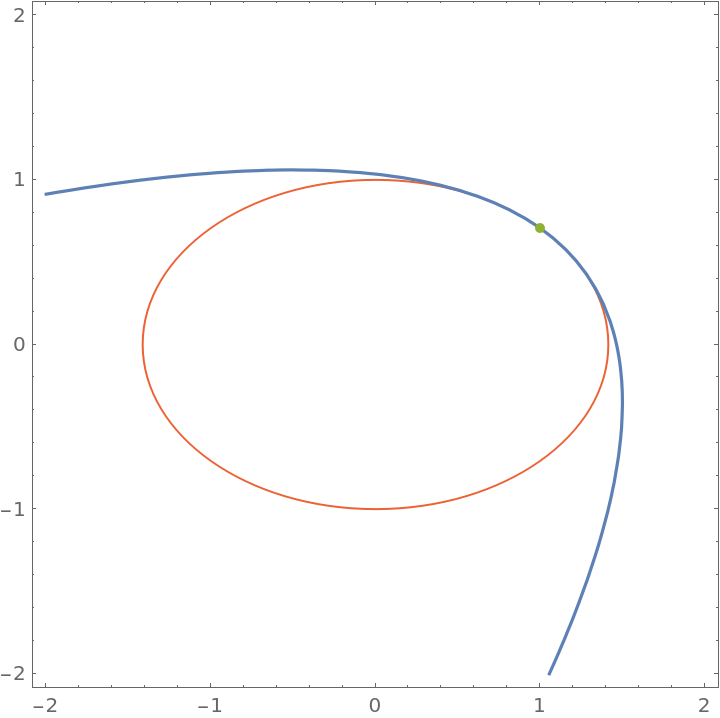
|
This work is licensed under a Creative Commons Attribution 4.0 International License