Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the defining properties of the osculating circle for a curve at a point
ResourceFunction["OsculatingCircleProperties"][f,{x,a}, y] gives the osculating circle of the curve f at the point x=a with respect to the variables x and y. | |
ResourceFunction["OsculatingCircleProperties"][f,{x,a},{y,b}] gives the osculating circle of f at the point (a,b) with respect to the variables x and y. | |
ResourceFunction["OsculatingCircleProperties"][{f[t],g[t]},{t,t0},x,y] gives the osculating circle to the parameterized curve at the point t0. | |
ResourceFunction["OsculatingCircleProperties"][…,type] gives the property type of the osculating circle. |
Return the osculating circle for a given expression:
| In[1]:= |
| Out[1]= |  |
Return the osculating circle for a parametrically defined curve:
| In[2]:= |
| Out[2]= |  |
Return the osculating circle for an implicitly defined curve:
| In[3]:= |
| Out[3]= | 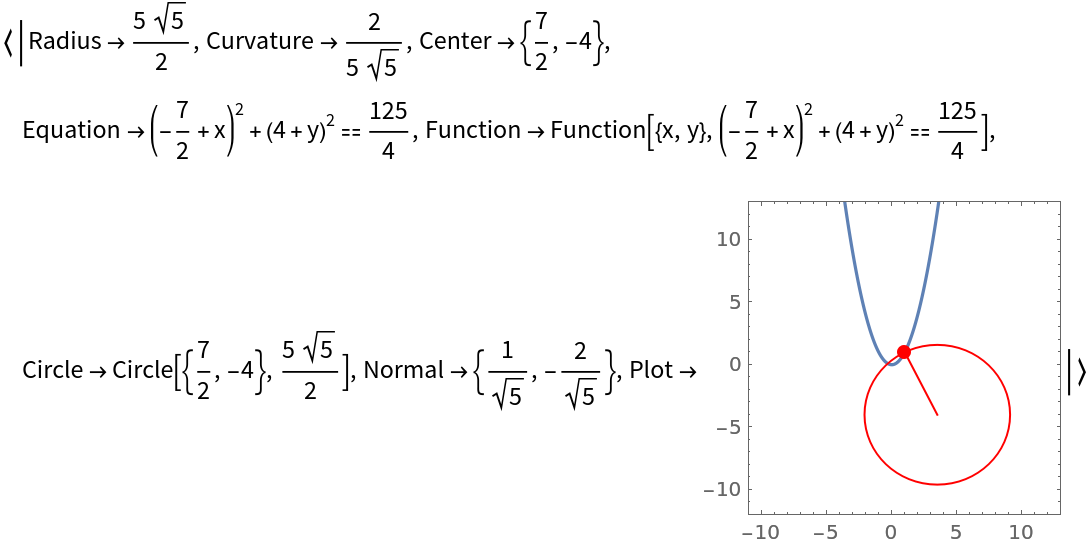 |
Return the osculating circle:
| In[4]:= |
| Out[4]= | 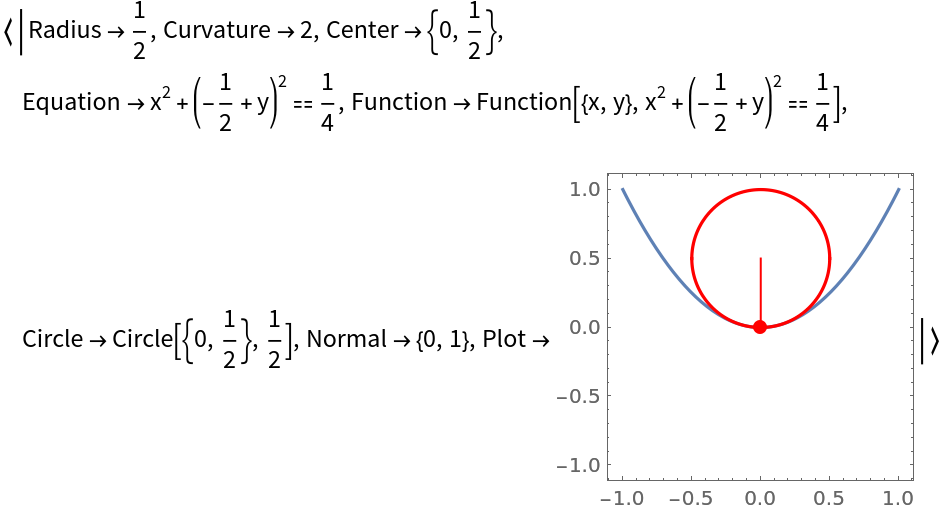 |
Return only the circle as a Graphics primitive:
| In[5]:= |
| Out[5]= |
Plot the osculating circle and expression:
| In[6]:= |
| Out[6]= | 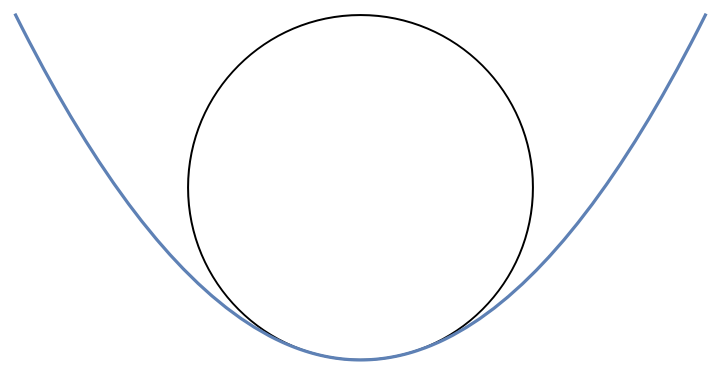 |
Or view the plot directly:
| In[7]:= |
| Out[7]= | 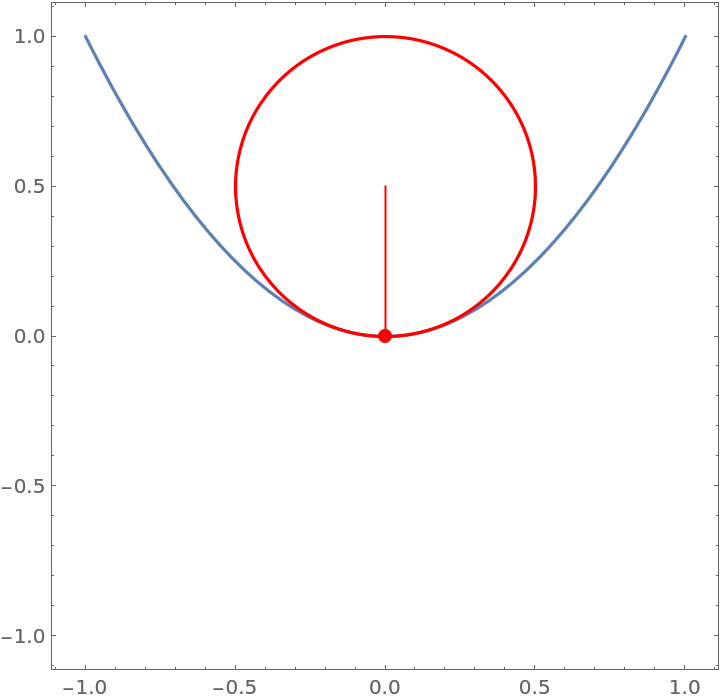 |
OsculatingCircleProperties returns unevaluated if the curvature does not exist at a given point:
| Out[8]= |
OsculatingCircleProperties returns unevaluated if the gradient is zero:
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License