Function Repository Resource:

OsculatingCircle

Source Notebook

Get the osculating circle of a curve

Contributed by: Alfred Gray, Eric W. Weisstein

ResourceFunction["OsculatingCircle"][c,t]

gives the osculating circle of a curve c depending on parameter t.

Examples

Basic Examples (1)

Plot a family of osculating circles to a logarithmic spiral, which is then highlighted by their presence:

In[1]:=

$logspiral[b_][t_] := {E^(b t) Cos[t], E^(b t) Sin[t]} logspiral[a_, b_][t_] := {a E^(b t) Cos[t], a E^(b t) Sin[t]}$

In[2]:=

Out[2]=

In[3]:=

$Graphics[{Hue[0], Table[ResourceFunction["OsculatingCircle"][logspiral[1, 1/2][t], t] /. t -> n \[Pi]/24, {n, -12, 12}]}, PlotRange -> All]$

Out[3]=

Scope (1)

Evolution in time of a family of osculating circles to a curve:

In[4]:=

$FullSimplify[ ResourceFunction["OsculatingCircle"][ 3/2 Entity["PlaneCurve", "Deltoid"][ EntityProperty["PlaneCurve", "ParametricEquations"]][2][t], t], 0 < t < 2 \[Pi]]$

Out[4]=

In[5]:=

$Graphics[{Table[ Circle[{6 Cos[t] - 3 Cos[2 t], 6 (1 + Cos[t]) Sin[t]}, 8 Abs[Sin[(3 t)/2]]], {t, 0, 2 \[Pi], .05}], ParametricPlot[{2 Cos[t] + Cos[2 t], 2 Sin[t] - Sin[2 t]}, {t, 0, 2 \[Pi]}, PlotStyle -> {Red, Thickness[.01]}][[1]]}]$

Out[5]=

In[6]:=

$Animate[Show[ Graphics[Circle[{6 Cos[t] - 3 Cos[2 t], 6 (1 + Cos[t]) Sin[t]}, 8 Abs[Sin[(3 t)/2]]], PlotRange -> {{-17., 12.5}, {-15.8, 15.8}}], ParametricPlot[{2 Cos[t0] + Cos[2 t0], 2 Sin[t0] - Sin[2 t0]}, {t0, 0, t}, PlotStyle -> {Red, Thickness[.01]}]], {t, .05, 2 \[Pi], .05}]$

Out[6]=

Publisher

Enrique Zeleny

Version History

1.0.0 – 25 March 2020

License Information

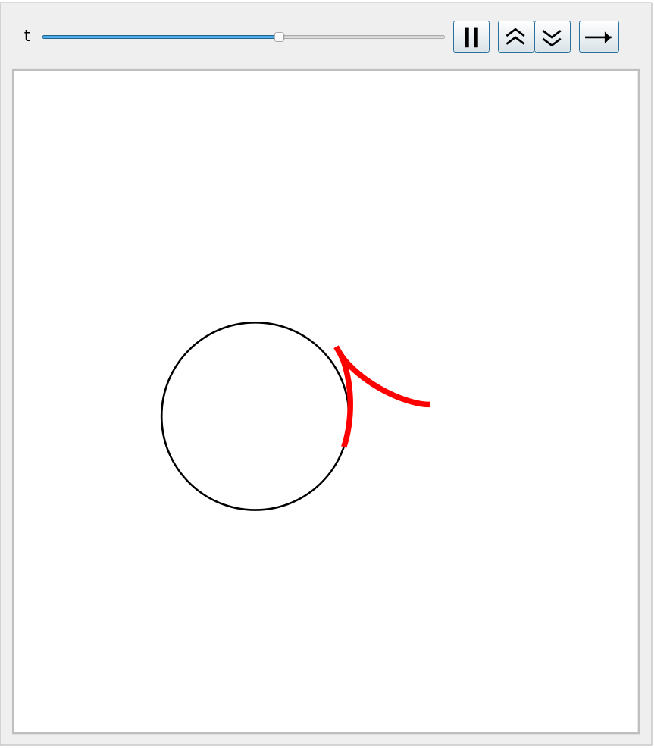This work is licensed under a Creative Commons Attribution 4.0 International License