Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 OrthogonalPolynomialData

Source Notebook

Return properties of orthogonal polynomials

Contributed by: Jan Mangaldan

ResourceFunction["OrthogonalPolynomialData"][poly,"property"]

gives the value of the specified property for the orthogonal polynomial poly.

Details

Named orthogonal polynomials can be specified as strings such as "Legendre" and "ChebyshevFirst". Symbols such as LegendreP and ChebyshevT are also supported.
Orthogonal polynomials with additional parameters can be specified in the form {"name",c1,…}, such as {"Jacobi",a,b}.
ResourceFunction["OrthogonalPolynomialData"][] and ResourceFunction["OrthogonalPolynomialData"][All] give a list of all available orthogonal polynomials.
ResourceFunction["OrthogonalPolynomialData"]["Properties"] gives a list of properties available for orthogonal polynomials.
Available properties include:
"DifferenceRoot"DifferenceRoot representation
"LeadingCoefficient"coefficient of the highest-order term
"MonicRecursionCoefficientB"recursion coefficient 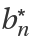for the monic polynomial
"MonicRecursionCoefficientC"recursion coefficient 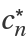for the monic polynomial
"NormalizationFactor"normalization factor
"OrthogonalityInterval"interval of orthogonality
"RecursionCoefficientA"recursion coefficient an for the polynomial
"RecursionCoefficientB"recursion coefficient bn for the polynomial
"RecursionCoefficientC"recursion coefficient cn for the polynomial
"WeightFunction"weight function
Orthogonal polynomials pn(x) satisfy a recurrence relation of the form pn+1(x)=(anx+bn)pn(x)+cnpn-1(x), where an, bn and cn respectively correspond to the properties "RecursionCoefficientA", "RecursionCoefficientB" and "RecursionCoefficientC".
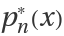
Monic polynomials , where the leading coefficient is 1, can be obtained by dividing a polynomial by the expression corresponding to the property "LeadingCoefficient".
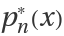
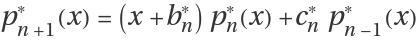
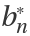
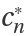
Monic polynomials , satisfy a recurrence relation of the form , where and respectively correspond to the properties "MonicRecursionCoefficientB" and "MonicRecursionCoefficientC".

Examples

Basic Examples (2) 

Return the DifferenceRoot representation of the Legendre polynomial:

In[1]:=
lp = ResourceFunction["OrthogonalPolynomialData"]["Legendre", "DifferenceRoot"]
Out[1]=

Compare with the result of LegendreP for the first few polynomials:

In[2]:=
Table[lp[x][n] == LegendreP[n, x] // Simplify, {n, 0, 10}]
Out[2]=

Scope (5) 

Normalization factor for the Gegenbauer polynomial:

In[3]:=
ResourceFunction[ "OrthogonalPolynomialData"][{"Gegenbauer", \[Lambda]}, \ "NormalizationFactor"]
Out[3]=

Use the symbol GegenbauerC to get the same result:

In[4]:=
ResourceFunction[ "OrthogonalPolynomialData"][{GegenbauerC, \[Lambda]}, \ "NormalizationFactor"]
Out[4]=

Supply the orthogonal polynomial as a pure function:

In[5]:=
ResourceFunction[ "OrthogonalPolynomialData"][{n, x} |-> JacobiP[n, \[Alpha], \[Beta], x], "WeightFunction"]
Out[5]=

Supply the orthogonal polynomial as an entity:

In[6]:=
ResourceFunction["OrthogonalPolynomialData"][ Entity["WolframLanguageSymbol", "ChebyshevU"], "WeightFunction"]
Out[6]=

Show all available orthogonal polynomials:

In[7]:=
ResourceFunction["OrthogonalPolynomialData"][All]
Out[7]=

Show all available properties:

In[8]:=
ResourceFunction["OrthogonalPolynomialData"]["Properties"]
Out[8]=

Applications (3) 

Verify the recurrence relation for the Jacobi polynomial:

In[9]:=
With[{a = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "RecursionCoefficientA"], b = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "RecursionCoefficientB"], c = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "RecursionCoefficientC"]}, JacobiP[n + 1, \[Alpha], \[Beta], x] == (a[n] x + b[n]) JacobiP[n, \[Alpha], \[Beta], x] + c[n] JacobiP[n - 1, \[Alpha], \[Beta], x]] // FunctionExpand // FullSimplify
Out[9]=

Verify the recurrence relation for the monic Jacobi polynomial:

In[10]:=
With[{h = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "LeadingCoefficient"], b = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "MonicRecursionCoefficientB"], c = ResourceFunction[ "OrthogonalPolynomialData"][{JacobiP, \[Alpha], \[Beta]}, "MonicRecursionCoefficientC"]}, JacobiP[n + 1, \[Alpha], \[Beta], x]/ h[n + 1] == (x + b[n]) JacobiP[n, \[Alpha], \[Beta], x]/h[n] + c[n] JacobiP[n - 1, \[Alpha], \[Beta], x]/h[n - 1]] // FunctionExpand // FullSimplify
Out[10]=

Verify the orthogonality relation for the associated Laguerre polynomial:

In[11]:=
With[{n = 5, a = 1}, Table[Integrate[ ResourceFunction["OrthogonalPolynomialData"][{"Laguerre", a}, "WeightFunction"][t] LaguerreL[j, a, t] LaguerreL[k, a, t], {t, Sequence @@ ResourceFunction["OrthogonalPolynomialData"][{"Laguerre", a}, "OrthogonalityInterval"][[1]]}] == ResourceFunction["OrthogonalPolynomialData"][{"Laguerre", a}, "NormalizationFactor"][k] KroneckerDelta[j, k], {j, 0, n}, {k, 0, n}]]
Out[11]=

Possible Issues (1) 

If a polynomial or property is not supported, Missing is returned:

In[12]:=
ResourceFunction["OrthogonalPolynomialData"]["xxx", "WeightFunction"]
Out[12]=
In[13]:=
ResourceFunction["OrthogonalPolynomialData"]["Legendre", "xxx"]
Out[13]=

Neat Examples (1) 

Verify the Christoffel-Darboux identity for the associated Laguerre polynomial:

In[14]:=
With[{n = 5, h = ResourceFunction["OrthogonalPolynomialData"][{"Laguerre", a}, "NormalizationFactor"], k = ResourceFunction["OrthogonalPolynomialData"][{"Laguerre", a}, "LeadingCoefficient"]}, \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n\)] \*FractionBox[\(LaguerreL[j, a, x] LaguerreL[j, a, y]\), \(h[ j]\)]\) == 1/h[n] k[n]/ k[n + 1] Cancel[ 1/(x - y) (LaguerreL[n, a, y] LaguerreL[n + 1, a, x] - LaguerreL[n + 1, a, y] LaguerreL[n, a, x])] // FullSimplify]
Out[14]=

Version History

  • 1.0.0 – 05 April 2021

Source Metadata

  • Citation:
    • Chihara T.S., An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, 1978.
    • Gautschi W., Orthogonal Polynomials: Computation and Approximation. Oxford: Oxford University Press, 2004.

Author Notes

Support for orthogonal polynomials that are currently not built into Mathematica (e.g. Hahn, Askey-Wilson classes) will eventually be added.

License Information