Function Repository Resource:

OrthogonalPolynomialCoefficientConvert

Convert coefficients of a series with respect to one orthogonal polynomial basis into another

Contributed by: Jan Mangaldan

ResourceFunction["OrthogonalPolynomialCoefficientConvert"][poly,x,basis]

gives a list of coefficients c_i of the orthogonal polynomial series that is equal to poly, where p_i(x) is represented by the orthogonal polynomial basis.

ResourceFunction["OrthogonalPolynomialCoefficientConvert"][cof,basis₁→basis₂]

gives a list of coefficients of the orthogonal polynomial series that is equal to , where c_i is the (i+1)^th element of the list cof and p_i(x) and are respectively represented by the orthogonal polynomials basis₁ and basis₂.

Details

The following polynomial bases are supported:

"Monomial"

monomial basis xⁱ

"ChebyshevFirst"

Chebyshev polynomial of the first kind ChebyshevT[i,x]

"ChebyshevSecond"

Chebyshev polynomial of the second kind ChebyshevU[i,x]

"Hermite"

Hermite polynomial HermiteH[i,x]

"Laguerre"

Laguerre polynomial LaguerreL[i,x]

"Legendre"

Legendre polynomial LegendreP[i,x]

{"Gegenbauer",m}

Gegenbauer polynomial GegenbauerC[i,m,x]

{"Laguerre",a}

associated Laguerre polynomial LaguerreL[i,a,x]

{"Jacobi",a,b}

Jacobi polynomial JacobiP[i,a,b,x]

Strings in specifications like "Monomial" and {"Jacobi",a,b} can be replaced with the corresponding symbols, as in Power and {JacobiP,a,b}.

Examples

Basic Examples (2)

Get the coefficients of a polynomial in the Legendre basis:

In[1]:=

Out[1]=

Verify that the Legendre coefficients reproduce the original polynomial:

In[2]:=

Out[2]=

Convert coefficients for a Laguerre series to coefficients for a Chebyshev series of the first kind:

In[3]:=

c2 = ResourceFunction["OrthogonalPolynomialCoefficientConvert"][
c1 = {4/15, -(7/15), 9/5, -(12/5), 4/5}, "Laguerre" -> "ChebyshevFirst"]

Out[3]=

Verify the equivalence:

In[4]:=

Out[4]=

Scope (2)

Convert a Laguerre series with symbolic coefficients and parameters to a Hermite series:

In[5]:=

Out[5]=

An equivalent specification:

In[6]:=

Out[6]=

Convert monomial basis coefficients to coefficients for a Chebyshev series of the second kind:

In[7]:=

Out[7]=

An equivalent specification:

In[8]:=

Out[8]=

Properties and Relations (2)

Converting an orthogonal polynomial series to the monomial basis is equivalent to expanding the series out and getting its coefficients:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

OrthogonalPolynomialCoefficientConvert can be used as its own inverse:

In[11]:=

Out[11]=

In[12]:=

Out[12]=

Neat Examples (1)

Express a Jacobi series in terms of another Jacobi series with different parameters:

In[13]:=

$ResourceFunction["OrthogonalPolynomialCoefficientConvert"][ Array[C, 3, 0], {"Jacobi", Subscript[\[Alpha], 1], Subscript[\[Beta], 1]} -> {"Jacobi", Subscript[\[Alpha], 2], Subscript[\[Beta], 2]}] // Simplify$

Out[13]=

Version History

1.0.0 – 05 April 2021

Source Metadata

Citation:
- Salzer H.E., "A recurrence scheme for converting from one orthogonal expansion into another." Communications of the ACM, vol. 16, no. 11, 705–707, 1973. DOI: 10.1145/355611.362548

Related Resources

License Information

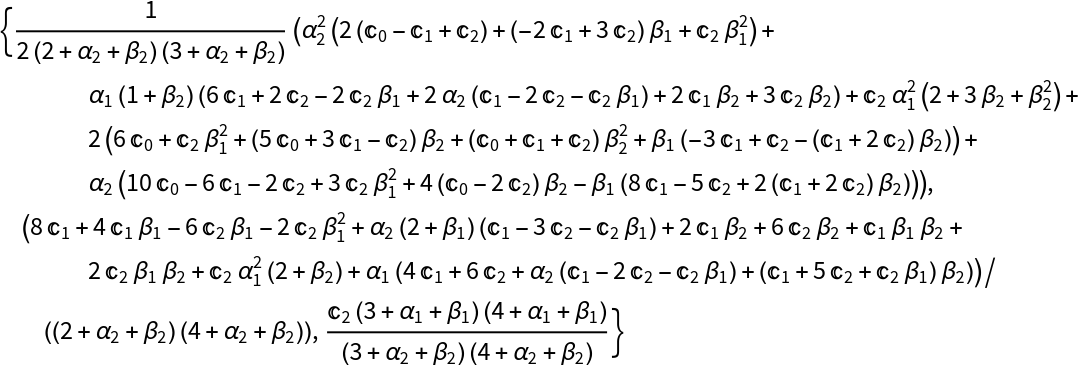
This work is licensed under a Creative Commons Attribution 4.0 International License