Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the best fitting line with respect to orthogonal distance
ResourceFunction["OrthogonalLineFit"][data] finds the best fitting orthogonal distance regression line to data. |
Parameters for a 2D line:
| In[1]:= |
| Out[1]= |
Generate some points near the line:
| In[2]:= |
| Out[2]= |  |
Find the orthogonal distance regression line:
| In[3]:= |
| Out[3]= |
Compare the regression line and the true line with the data:
| In[4]:= | ![Legended[
Graphics[{{Directive[AbsolutePointSize[6], Brown], Point[pts]},
{Directive[AbsoluteThickness[2], ColorData[97, 1]], ofit},
{Directive[AbsoluteThickness[2], ColorData[97, 3]], InfiniteLine[p0, v0]}}, Frame -> True, PlotRangeClipping -> True],
LineLegend[{ColorData[97, 1], ColorData[97, 3]}, {"orthogonal fit", "true line"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/115/115b0475-c4a7-41e2-aca2-d63d90fe1a4c/7ef3d273cf4609b2.png) |
| Out[4]= | 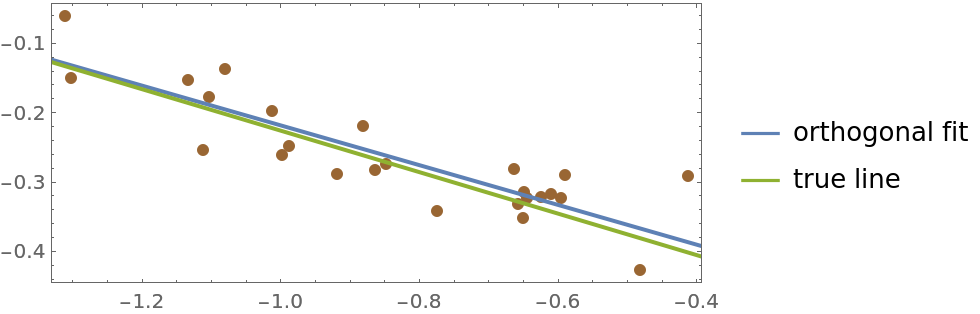 |
Parameters for a 3D line:
| In[5]:= |
| Out[5]= |
Generate some points near the line:
| In[6]:= |
| Out[6]= |  |
Find the orthogonal distance regression line:
| In[7]:= |
| Out[7]= |
Compare the regression line and the true line with the data:
| In[8]:= | ![Legended[
Graphics3D[{{Directive[AbsolutePointSize[6], Brown], Point[pts]},
{Directive[AbsoluteThickness[2], ColorData[97, 1]], ofit},
{Directive[AbsoluteThickness[2], ColorData[97, 3]], InfiniteLine[p0, v0]}}, Axes -> True],
LineLegend[{ColorData[97, 1], ColorData[97, 3]}, {"orthogonal fit", "true line"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/115/115b0475-c4a7-41e2-aca2-d63d90fe1a4c/34a09ef019dea07c.png) |
| Out[8]= | 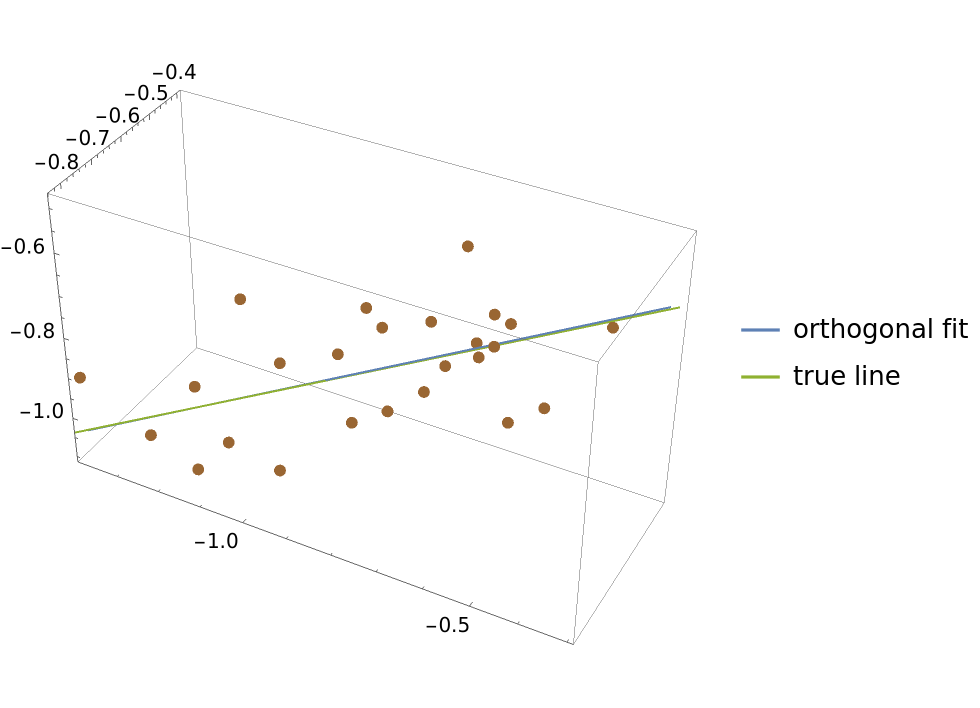 |
Here is a list of values:
| In[9]:= |
When coordinates are not given, OrthogonalLineFit assumes the values are to be paired up with 1,2,…:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= | 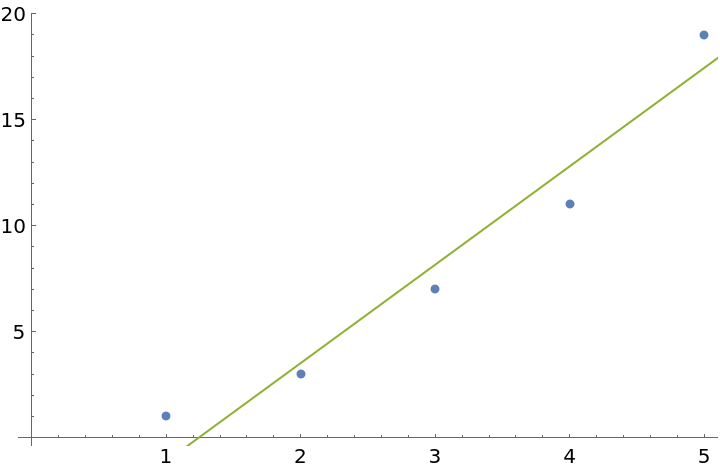 |
Here is some data:
| In[12]:= |
This computes the parameters for the orthogonal distance regression line using the definition:
| In[13]:= | ![{pm, vm} = Partition[
NArgMin[Total[
RegionDistance[InfiniteLine[{px, py}, {vx, vy}], #]^2 & /@ data], {px, py, vx, vy}], 2]](https://www.wolframcloud.com/obj/resourcesystem/images/115/115b0475-c4a7-41e2-aca2-d63d90fe1a4c/626393a089c9c390.png) |
| Out[13]= |
Use OrthogonalLineFit to get the best-fit line:
| In[14]:= |
| Out[14]= |
Use RegionMember to compare the equations for the best fit line generated by both methods:
| In[15]:= |
| Out[15]= |
Construct a function from the orthogonal fit:
| In[16]:= |
| Out[16]= |
Compare the orthogonal fit with the conventional least-squares fit:
| In[17]:= |
| Out[17]= |
| In[18]:= | ![Plot[{oFun[x], lFun[x]}, {x, 0, 5}, Epilog -> {Directive[AbsolutePointSize[4], ColorData[97, 4]], Point[data]}, PlotLegends -> {"orthogonal fit", "least-squares fit"}]](https://www.wolframcloud.com/obj/resourcesystem/images/115/115b0475-c4a7-41e2-aca2-d63d90fe1a4c/04597bf858a873c4.png) |
| Out[18]= | 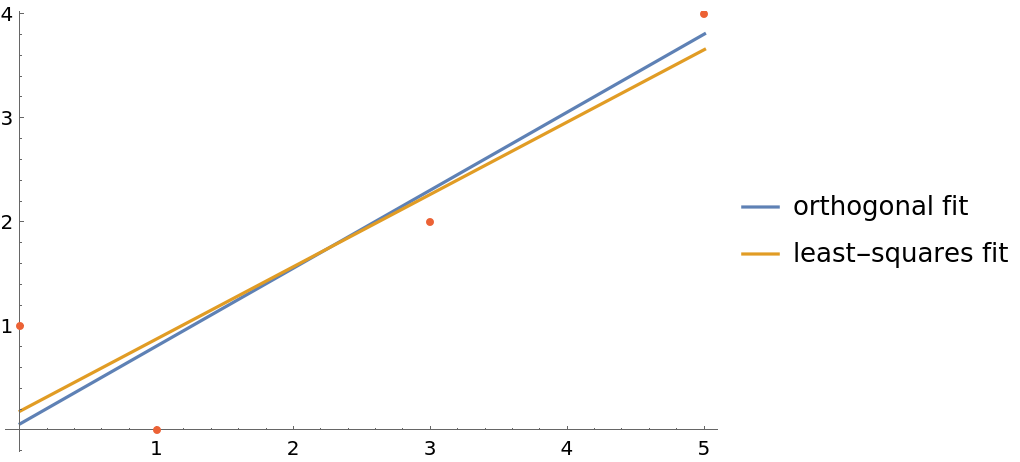 |
This work is licensed under a Creative Commons Attribution 4.0 International License