Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Give the index of an ordered tuple
ResourceFunction["OrderedTupleIndex"][tuple] gives the index of the ordered tuple. |
The following ordered 3-tuple sequence can be extended to infinity:
| In[1]:= |
| Out[1]= |
The function returns indices of one to ten for these ordered tuples:
| In[2]:= |
| Out[2]= |
Any nondecreasing list of nonnegative integers can be considered as an ordered tuple with a unique index:
| In[3]:= |
| Out[3]= |
The result above is an ordered tuple with a unique index:
| In[4]:= |
| Out[4]= |
Here are some ordered 2-tuples with their indices to show their structure:
| In[5]:= | ![doubles = # - {0, 1} & /@ SortBy[Subsets[Range[0, 5], {2}], Reverse];
Graphics[{Text[
Style[Column[{StringJoin[ToString /@ #], ResourceFunction["OrderedTupleIndex"][#]},
Alignment -> Center], 20], #] & /@ doubles, Blue, Line[doubles]}]](https://www.wolframcloud.com/obj/resourcesystem/images/49b/49ba7190-7cb9-46d9-b6ec-036640cc2b0d/40edc723b85227f9.png) |
| Out[5]= | 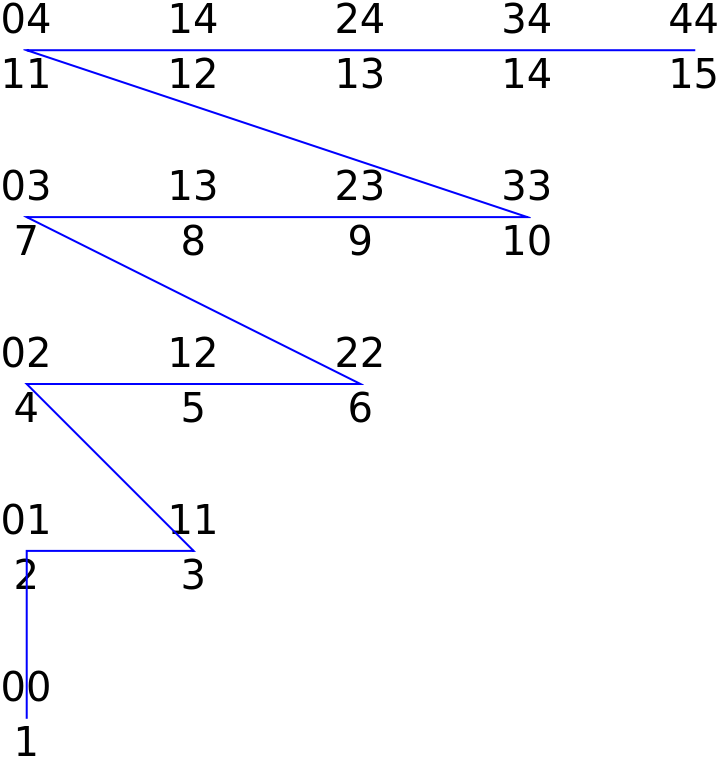 |
The ordered 2-tuple {4,4} has an index of ![]() :
:
| In[6]:= |
| Out[6]= |
OrderedTupleIndex returns the same thing:
| In[7]:= |
| Out[7]= |
The structure of ordered 3-tuples in 3D:
| In[8]:= | ![triples = # - {0, 1, 2} & /@ SortBy[Subsets[Range[0, 5], {3}], Reverse];
Graphics3D[{Text[
Style[Column[{StringJoin[ToString /@ #], ResourceFunction["OrderedTupleIndex"][#]},
Alignment -> Center], 20], #] & /@ triples, Blue, Line[triples]}]](https://www.wolframcloud.com/obj/resourcesystem/images/49b/49ba7190-7cb9-46d9-b6ec-036640cc2b0d/62dd41dcb1587981.png) |
| Out[8]= | 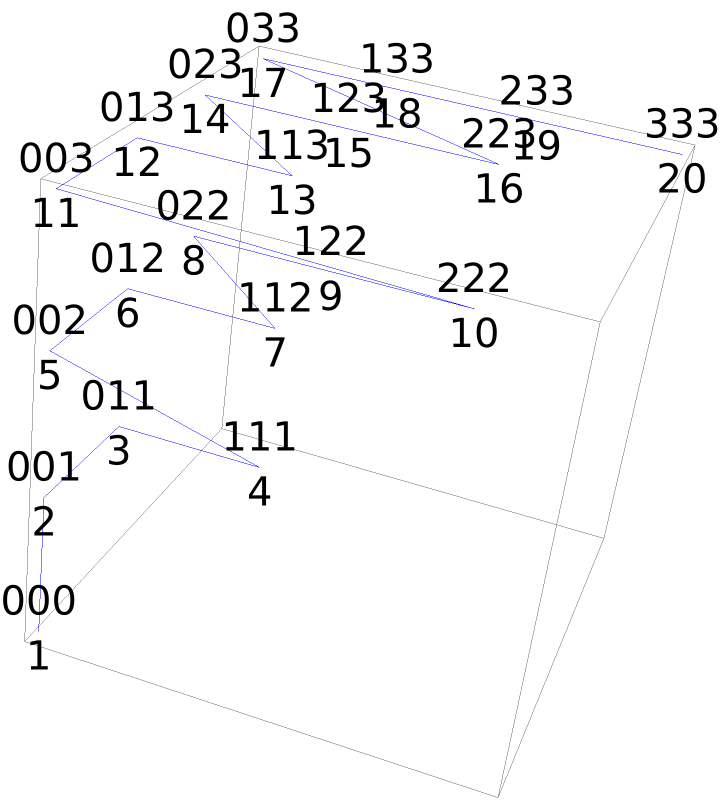 |
This work is licensed under a Creative Commons Attribution 4.0 International License