Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the ordered Schur decomposition of a matrix
ResourceFunction["OrderedSchurDecomposition"][m] yields the ordered Schur decomposition for a numerical matrix m, given as a list {q,t} where q is an orthonormal matrix and t is a block upper‐triangular matrix. | |
ResourceFunction["OrderedSchurDecomposition"][{m,a}] gives the generalized Schur decomposition of the matrix pencil {m,a}, where m and a are numerical matrices. |
| "Criteria" | "Magnitude" | criterion used for ordering diagonal elements in the triangular factor |
| "Order" | "Decreasing" | whether to sort in increasing or decreasing order |
| Pivoting | False | whether to perform pivoting |
| RealBlockDiagonalForm | True | whether to use real blocks instead of complex values for real matrices |
| "Magnitude" | sort diagonal elements by magnitude |
| "RealPart" | sort diagonal elements by their real parts |
| "AbsRealPart" | sort diagonal elements by the absolute values of their real parts |
| "AbsImaginaryPart" | sort diagonal elements by the absolute values of their imaginary parts |
| "Decreasing" | sort in decreasing order |
| "Increasing" | sort in increasing order |
The ordered Schur decomposition of a real matrix:
| In[1]:= |
| Out[1]= |
Compare with the result of SchurDecomposition:
| In[2]:= |
| Out[2]= |
A 4×4 matrix with real entries:
| In[3]:= | ![m = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"3", "1", "2", "5"},
{"2", "1", "3", "7"},
{"3", "1", "2", "4"},
{"4", "1", "3", "2"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\);](https://www.wolframcloud.com/obj/resourcesystem/images/86b/86bb57b1-1782-4727-86a1-1fc7912f8d2b/0efd6430278a72ca.png) |
Compute the ordered Schur decomposition with machine precision, with the diagonal elements sorted in decreasing order of magnitude:
| In[4]:= |
| Out[4]= |  |
Compute the ordered Schur decomposition with 24-digit arbitrary precision:
| In[5]:= |
| Out[5]= |  |
Sort the diagonal elements by their real parts, in increasing order:
| In[6]:= |
| Out[6]= | 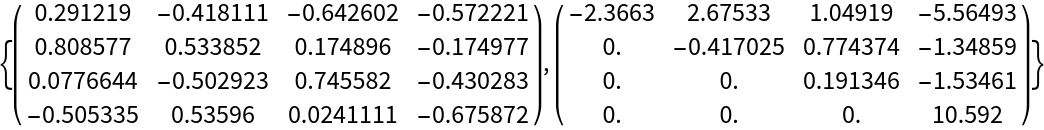 |
A 3×3 matrix with complex entries:
| In[7]:= |  |
Ordered Schur decomposition of a complex matrix, with the diagonal elements sorted in decreasing order of magnitude:
| In[8]:= |
| Out[8]= |  |
Sort the diagonal elements by the magnitude of their imaginary parts, in increasing order:
| In[9]:= |
| Out[9]= |  |
Compute the ordered generalized Schur decomposition for a matrix pencil:
| In[10]:= | ![ResourceFunction["OrderedSchurDecomposition"][N@{( {
{1, 7, 3},
{2, 9, 12},
{5, 22, 7}
} ), ( {
{1, 2, 3},
{13, 6, 4},
{1, 8, 15}
} )}] // Map[MatrixForm]](https://www.wolframcloud.com/obj/resourcesystem/images/86b/86bb57b1-1782-4727-86a1-1fc7912f8d2b/647f684885de84e7.png) |
| Out[10]= |  |
Use a different ordering:
| In[11]:= | ![ResourceFunction["OrderedSchurDecomposition"][N@{( {
{1, 7, 3},
{2, 9, 12},
{5, 22, 7}
} ), ( {
{1, 2, 3},
{13, 6, 4},
{1, 8, 15}
} )}, "Criteria" -> "RealPart", "Order" -> "Increasing"] // Map[MatrixForm]](https://www.wolframcloud.com/obj/resourcesystem/images/86b/86bb57b1-1782-4727-86a1-1fc7912f8d2b/0ccd6c26c0d5aa2e.png) |
| Out[11]= | 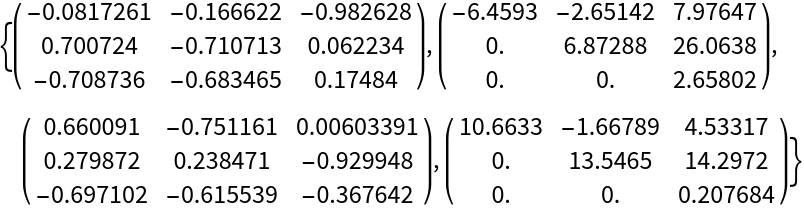 |
m is a matrix with complex eigenvalues:
| In[12]:= |
| Out[13]= |
Sort the diagonal elements by their magnitude in decreasing order:
| In[14]:= |
| In[15]:= |
| Out[15]= |  |
Sort the diagonal elements by their real parts in decreasing order:
| In[16]:= |
| In[17]:= |
| Out[17]= |  |
Sort the diagonal elements by the magnitude of their imaginary parts:
| In[18]:= |
| In[19]:= |
| Out[19]= |  |
m is a matrix with positive eigenvalues:
| In[20]:= |
| Out[21]= |
Sort the diagonal elements in decreasing order:
| In[22]:= |
| In[23]:= |
| Out[23]= |  |
Sort the diagonal elements in increasing order:
| In[24]:= |
| In[25]:= |
| Out[25]= |  |
m is a 3×3 matrix:
| In[26]:= |
With Pivoting→True, an extra matrix that represents the scaling and permutation is returned:
| In[27]:= |
| Out[27]= |  |
| In[28]:= |
| Out[28]= |  |
Verify that m.d is equal to d.q.t.ConjugateTranspose[q]:
| In[29]:= |
| Out[29]= |
m is a matrix with two real and two complex eigenvalues:
| In[30]:= |
| Out[31]= |
With RealBlockDiagonalForm→False, the result is complex upper triangular:
| In[32]:= |
| In[33]:= |
| Out[33]= | 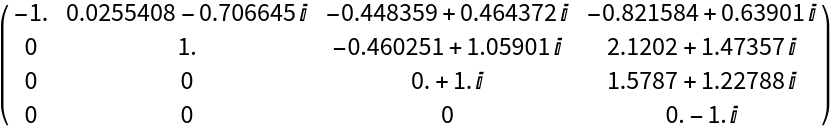 |
With RealBlockDiagonalForm→True, there are real 2×2 blocks along the diagonal:
| In[34]:= |
| In[35]:= |
| Out[35]= |  |
m is a matrix with two real and two complex eigenvalues:
| In[36]:= |
| Out[37]= |
Find the ordered Schur decomposition of m:
| In[38]:= |
| Out[38]= |  |
The real eigenvalues appear on the diagonal of t, the complex as a 2×2 block:
| In[39]:= |
| Out[39]= | 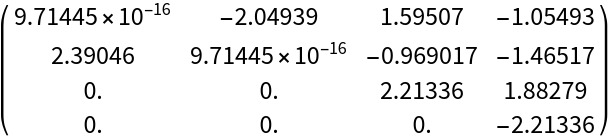 |
Verify that m is equal to q.t.ConjugateTranspose[q]:
| In[40]:= |
| Out[40]= |
A matrix pencil:
| In[41]:= | ![{m, a} = N[{( {
{5, 6, -5},
{4, -3, 3},
{3, -2, 3}
} ), ( {
{16, -6, 5},
{5, -6, 16},
{3, -5, 6}
} )}];](https://www.wolframcloud.com/obj/resourcesystem/images/86b/86bb57b1-1782-4727-86a1-1fc7912f8d2b/35d3d628fbe17525.png) |
Find the ordered generalized Schur decomposition:
| In[42]:= |
| Out[42]= |  |
Verify that m is given by q.s.ConjugateTranspose[p]:
| In[43]:= |
| Out[43]= |
Verify that a is given by q.t.ConjugateTranspose[p]:
| In[44]:= |
| Out[44]= |
This work is licensed under a Creative Commons Attribution 4.0 International License