Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 OpticalFieldModeling

Source Notebook

Model non-paraxial optical field interference and diffraction experiments under arbitrary spatial coherence

Contributed by: Julián Laverde

ResourceFunction["OpticalFieldModeling"][points]

returns a point array object representing real points points and their corresponding virtual points.

ResourceFunction["OpticalFieldModeling"][points,λ,z]

returns a power spectrum object representing the power spectrum of points at wavelength λ and propagation distance z.

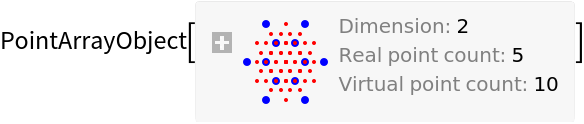
Details and Options

The points can be a list of numeric or Quantity coordinates, or a QuantityArray.
If points is given as a numeric list, the values are taken to be in micrometers.
ResourceFunction["OpticalFieldModeling"] takes the following options:
"CoherenceFunction" None calculates the phase of every real point light source
"PhaseFunction" None calculates the complex degree of spatial coherence of every virtual point
"PhaseFunction" is supplied with the coordinates of each real point and should return a numerical value in radians.
With the default setting "PhaseFunction"→None, the phase value of every real point is set to 0, representing a plane wavefront.
"CoherenceFunction" is supplied with the distance vector of every length-2 subset of real points and should return a numerical value between 0 and 1.
With the default setting "CoherenceFunction"→None, the coherence value of every virtual point is set to 1, representing a fully spatially coherent light source.
The PointArrayObject expression returned by ResourceFunction["OpticalFieldModeling"] supports the following properties:
"PointPlot" a plot showing the locations of the real points and their corresponding virtual points
"PowerSpectrum" a PowerSpectrumObject based on the given wavelength and propagation distance
The "PowerSpectrum" property requires the arguments λ (wavelength) and z (propagation distance): PointArrayObject[…]["PowerSpectrum",λ,z]
The "PointPlot" property of PointArrayObject accepts the same options as the NumberLinePlot (for 1-dimensional point arrays) or ListPlot (for 2-dimensional point arrays) functions.
The PowerSpectrumObject expression returned by the "PowerSpectrum" property of a PointArrayObject supports the following properties:
"Expression" complete power spectrum expression
"Plot" power spectrum 1D plot along the horizontal axis
"DensityPlot" power spectrum density plot
The "Plot" and "DensityPlot" properties accept arguments for angle (in degrees) and plotting step: PowerSpectrumObject[…]["Plot",angle,step].
The angle specifies the maximum half-angle of the cone of light. If unspecified or set to Automatic, angle is taken by default to be 65°.
If unspecified or set to Automatic, step is calculated based on a fraction of the propagation distance of the PowerSpectrumObject.
The "Plot" and "DensityPlot" properties of PowerSpectrumObject accept the same options as the ListPlot and DensityPlot functions.

Examples

Basic Examples

Create a PointArrayObject with a set of real points:

In[1]:=
pointArray = ResourceFunction["OpticalFieldModeling"][N@CirclePoints[1, 4]]
Out[1]=

Calculate the power spectrum for a given wavelength and propagation distance:

In[2]:=
\[Lambda] = 0.632; powerSpectrum = pointArray["PowerSpectrum", \[Lambda], 10 \[Lambda]]
Out[3]=

Plot the power spectrum using "DensityPlot":

In[4]:=
powerSpectrum["DensityPlot", 70, \[Lambda]/3]
Out[4]=

Scope

Plot the given 2D real points array with its corresponding virtual points:

In[5]:=
circularPointArray = ResourceFunction["OpticalFieldModeling"][N@CirclePoints[1, 10]]; circularPointArray["PointPlot"]
Out[2]=

Plot the given 1D real points array with its corresponding virtual points:

In[6]:=
circularPointArray = ResourceFunction["OpticalFieldModeling"][N@Range[-1, 1]]; circularPointArray["PointPlot"]
Out[4]=

Plot the 1D power spectrum with "Plot":

In[7]:=
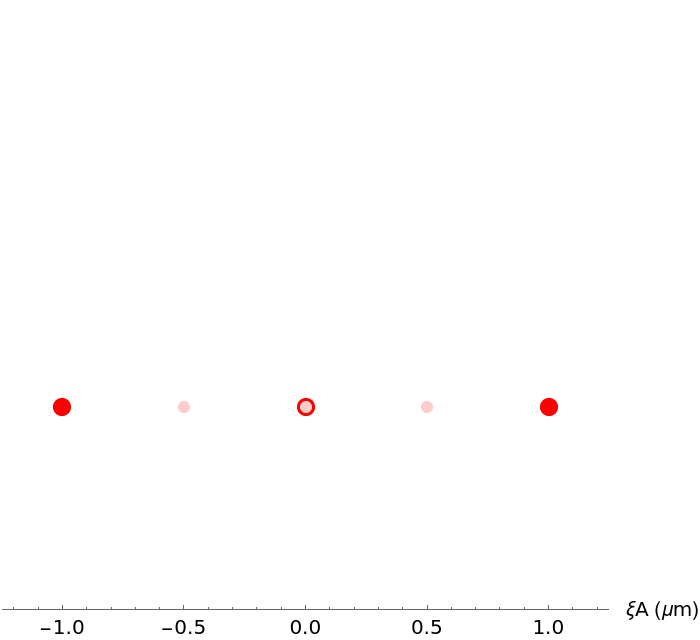
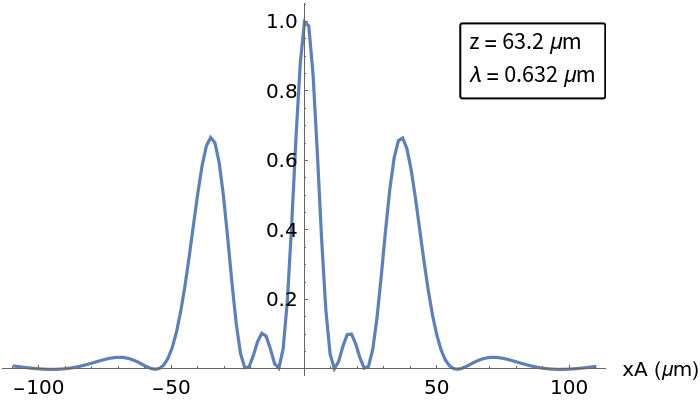
\[Lambda] = 0.632; pointArray1D = ResourceFunction["OpticalFieldModeling"][ N@Range[-2 \[Lambda], 2 \[Lambda], 2 \[Lambda]]]; powerSpectrum1D = pointArray1D["PowerSpectrum", \[Lambda], 100 \[Lambda]]; powerSpectrum1D["Plot", 60, 1.6]
Out[4]=

Options

PhaseFunction

The phase function can be given as a symbol:

In[8]:=
phaseF[\[Xi]A_] := RandomReal[{0, 2 \[Pi]}]; ResourceFunction["OpticalFieldModeling"][Range[-3, 3], "PhaseFunction" -> phaseF]
Out[2]=

Or as a pure function:

In[9]:=
ResourceFunction["OpticalFieldModeling"][RandomReal[3, {5, 2}], "PhaseFunction" -> (#1^2 + 1.5 #2 &)]
Out[9]=

By default, uniform phase distribution is assumed:

In[10]:=
ResourceFunction["OpticalFieldModeling"][Range[-3, 3]]
Out[10]=

CoherenceFunction

Use PDF to utilize a statistical distribution function as the coherence function:

In[11]:=
\[Sigma] = 2; ResourceFunction["OpticalFieldModeling"][Range[-3, 3], "CoherenceFunction" -> PDF@MaxwellDistribution[\[Sigma]]]
Out[2]=

The coherence function can be given as a symbol:

In[12]:=
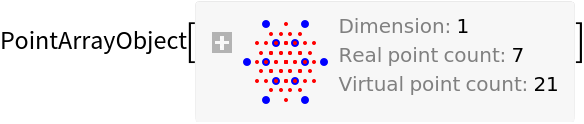
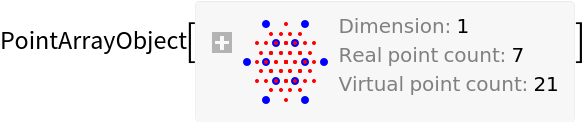
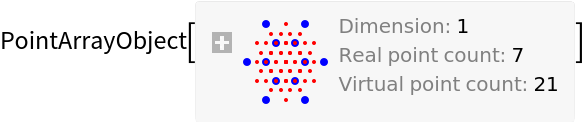
\[Sigma] = 2; coherenceF[\[Xi]D_] := N@Exp[-\[Xi]D^2/(2 \[Sigma]^2)]; ResourceFunction["OpticalFieldModeling"][Range[-3, 3], "CoherenceFunction" -> coherenceF]
Out[9]=

Os as a pure function:

In[13]:=
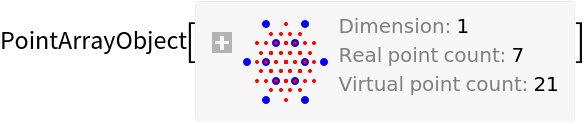
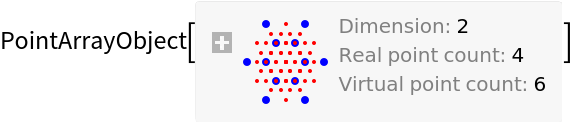
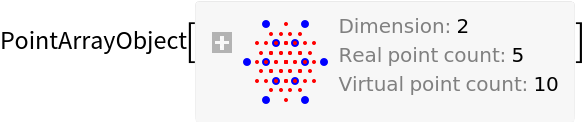
\[Sigma] = 2000; ResourceFunction["OpticalFieldModeling"][ QuantityArray[RandomReal[3, {5, 2}], "Millimeters"], "CoherenceFunction" -> (Exp[-((#1^2 + #2^2)/(2 \[Sigma]^2))] &)]
Out[14]=

By default, a fully coherent optical field is assumed:

In[15]:=
ResourceFunction["OpticalFieldModeling"][Range[-3, 3]]
Out[15]=

Applications

Simulate a vortex generation using a spiral phase mask:

In[16]:=
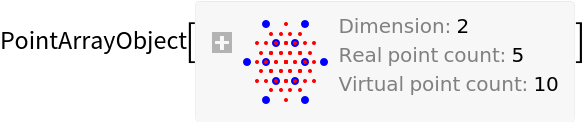
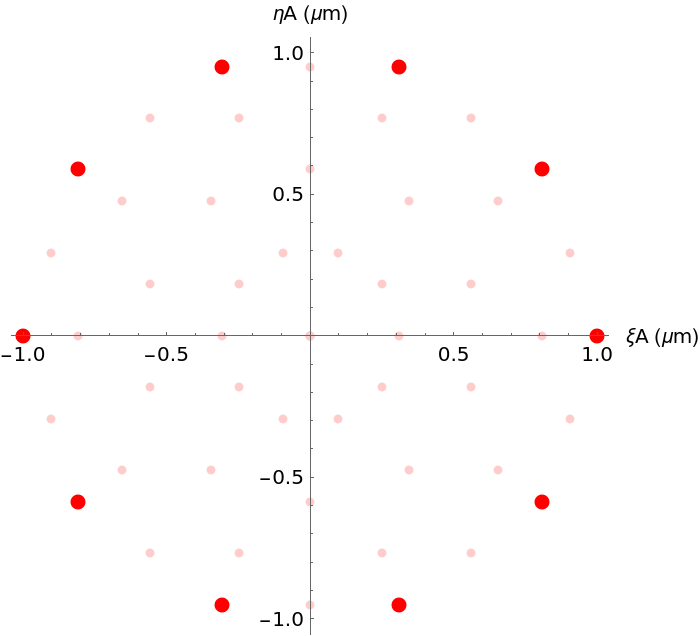
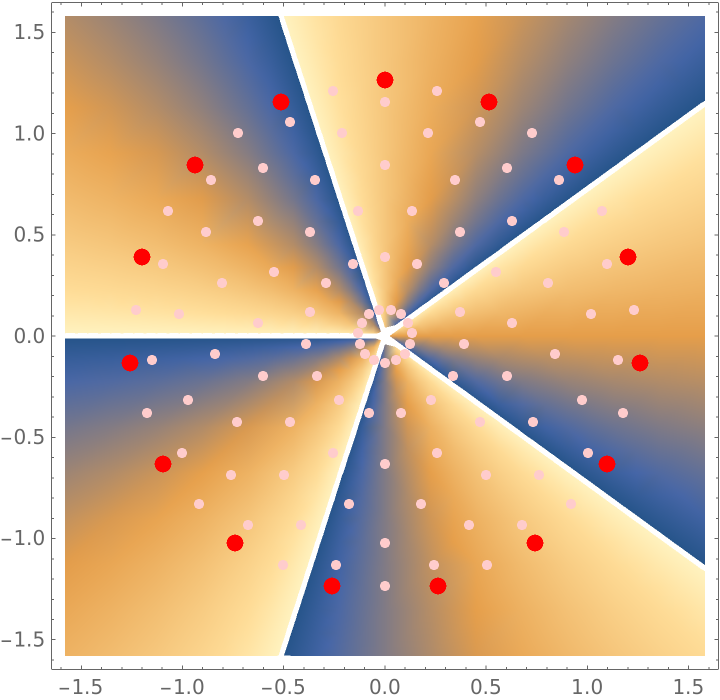
m = 5; vortexPointArray = ResourceFunction["OpticalFieldModeling"][ N@CirclePoints[2 \[Lambda], 15], "PhaseFunction" -> Function[{\[Xi]A, \[Eta]A}, Mod[m ArcTan[\[Xi]A, \[Eta]A] + \[Pi], 2 \[Pi]]]]
Out[2]=

Show the plot of real and virtual points superimposed over the phase mask:

In[17]:=
Show[DensityPlot[ Mod[m ArcTan[x, y] + \[Pi], 2 \[Pi]], {x, -2.5 \[Lambda], 2.5 \[Lambda]}, {y, -2.5 \[Lambda], 2.5 \[Lambda]}], vortexPointArray["PointPlot"]]
Out[17]=

Plot the power spectrum:

In[18]:=
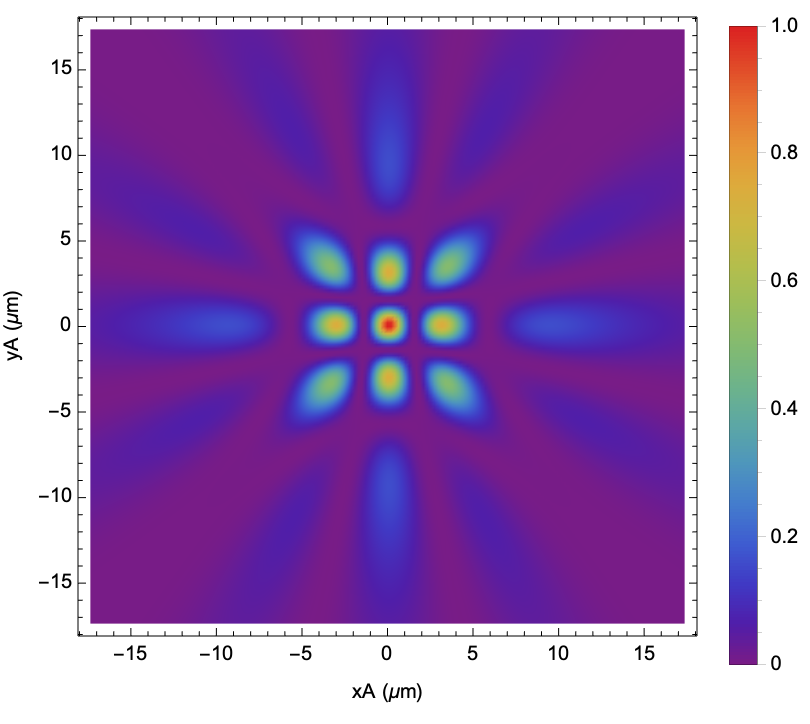
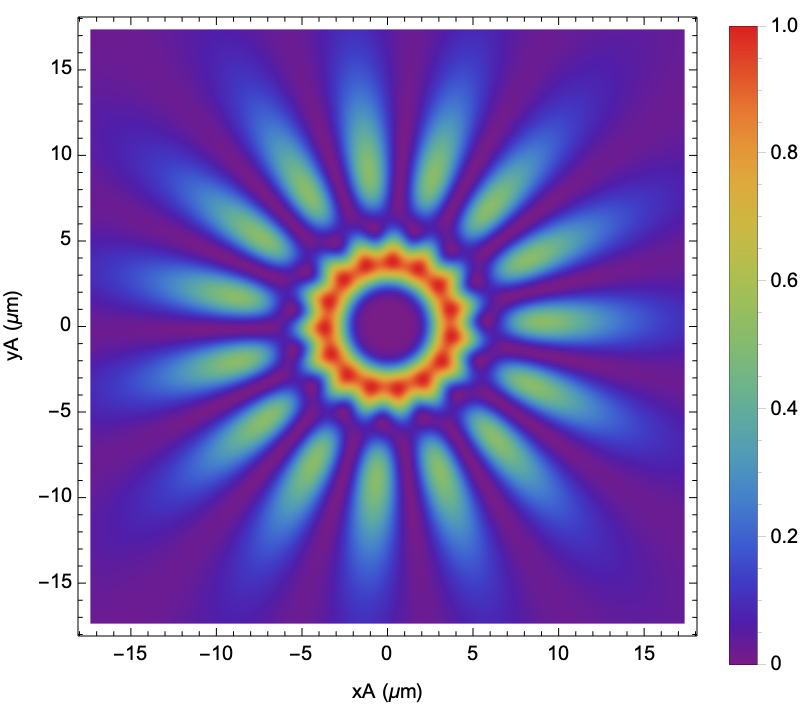
\[Lambda] = 0.632; z = 10 \[Lambda]; vortexPowerSpectrum = vortexPointArray["PowerSpectrum", \[Lambda], z]; vortexPowerSpectrum["DensityPlot", 70, z/40]
Out[21]=

Simulate the interference pattern produced by a grating illuminated with partially coherent light:

In[22]:=
\[Sigma] = 4 \[Lambda]; gratingPointArray = ResourceFunction["OpticalFieldModeling"][ Flatten[Table[{i, 0}, {i, -6 \[Lambda], 6 \[Lambda], 2 \[Lambda]}, {j, 1}], 1], "CoherenceFunction" -> Function[{\[Xi]D, \[Eta]D}, E^(-(\[Xi]D^2 + \[Eta]D^2)/( 2 \[Sigma]^2))]]
Out[22]=

Plot the power spectrum:

In[23]:=
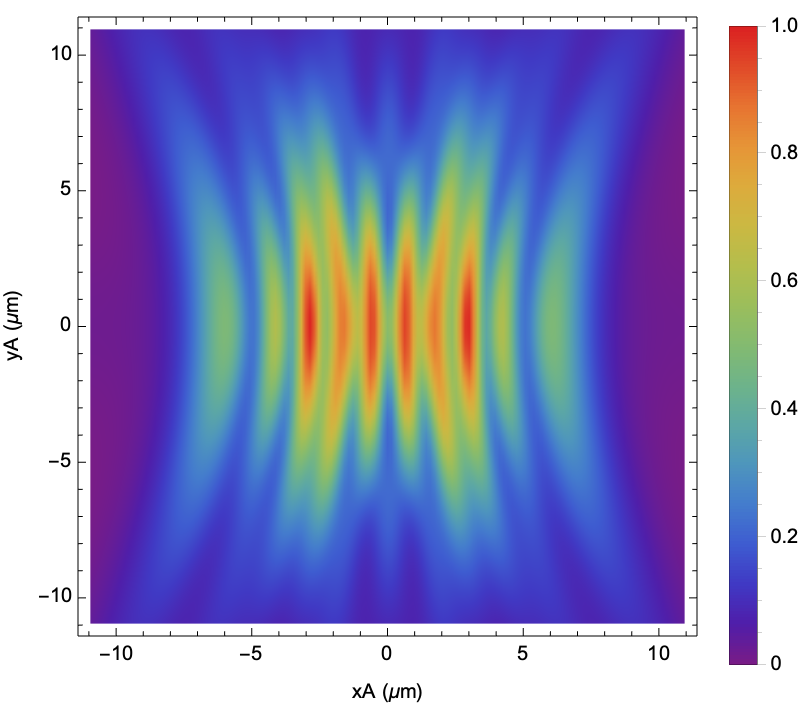
\[Lambda] = 0.632; z - 10 \[Lambda]; gratingPowerSpectrum = gratingPointArray["PowerSpectrum", \[Lambda], z]; gratingPowerSpectrum["DensityPlot", 60, z/40]
Out[24]=

Reproduce a speckle pattern:

In[25]:=
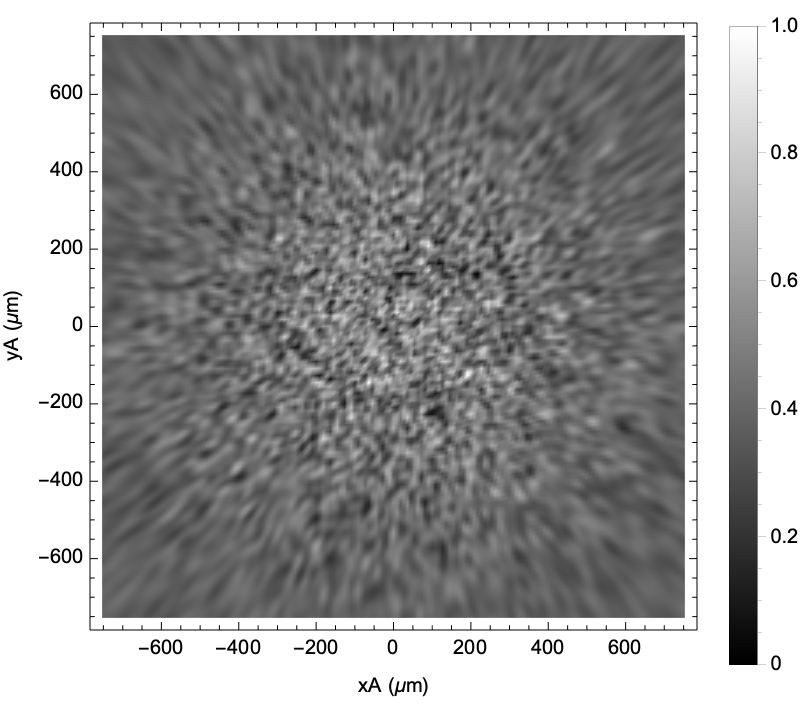
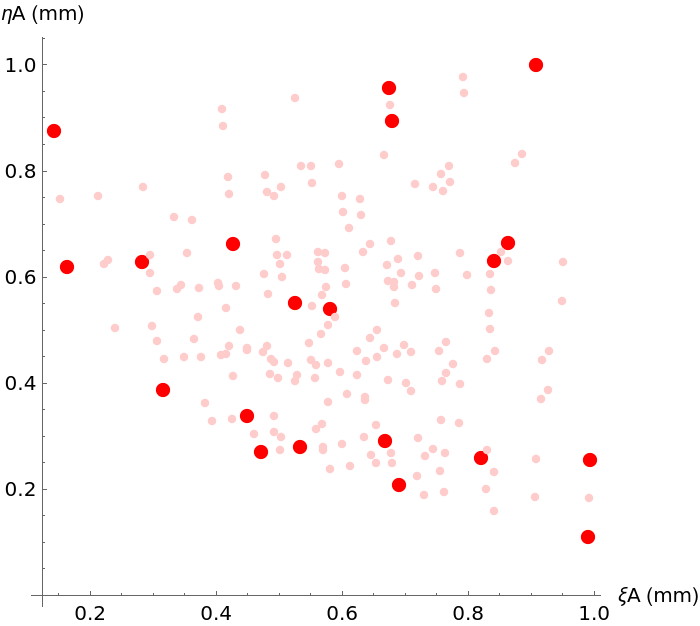
phaseF[\[Xi]A_, \[Eta]A_] := RandomReal[{-\[Pi], \[Pi]}]; \[Lambda] = 0.632; speckleArray = ResourceFunction["OpticalFieldModeling"][ RandomPoint[Disk[{0, 0}, 20 \[Lambda]], 150], "PhaseFunction" -> phaseF]; specklePS = speckleArray["PowerSpectrum", \[Lambda], 1000 \[Lambda]]; specklePS["DensityPlot", 50, ColorFunction -> GrayLevel]
Out[18]=

Properties and Relations

Use QuantityArray to specify the units of the input real points list:

In[26]:=
ResourceFunction["OpticalFieldModeling"][ QuantityArray[RandomReal[1, {20, 2}], "Millimeters"]]["PointPlot"]
Out[26]=

Use Quantity to specify the units of the wavelength and propagation distance:

In[27]:=
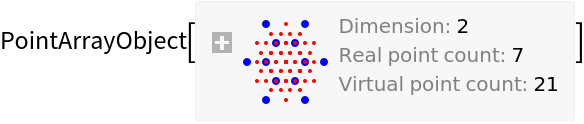
\[Lambda] = 520; z = 10 \[Lambda]; ResourceFunction["OpticalFieldModeling"][ QuantityArray[RandomReal[1, {20, 2}], "Millimeters"], Quantity[\[Lambda], "Nanometers"], Quantity[z, "Micrometers"]]
Out[17]=

Use "Expression" to get the complete symbolic expression from a power spectrum object:

In[28]:=
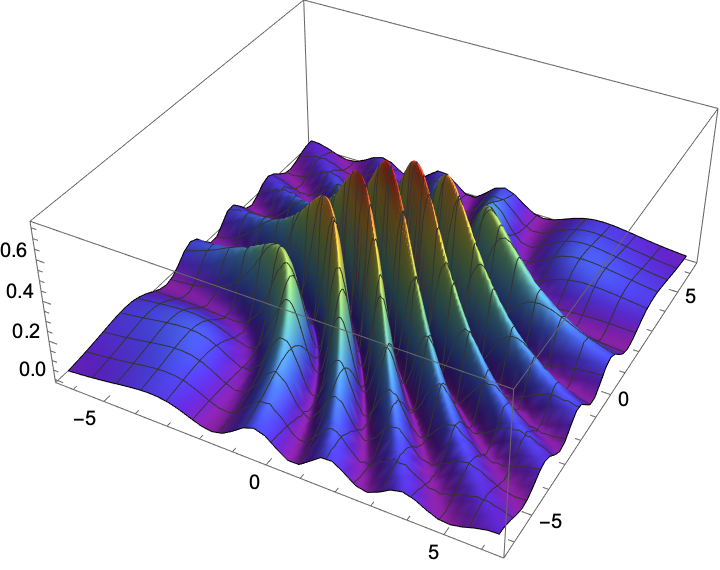
\[Lambda] = 0.632; pointArray = ResourceFunction["OpticalFieldModeling"][{{-1, -1}, {1, 1}}]; powerSpectrum = pointArray["PowerSpectrum", \[Lambda], 5 \[Lambda]]; powerSpectrum["Expression"]
Out[18]=

The expression can be supplied to any suitable visualization function:

In[29]:=
Plot3D[powerSpectrum["Expression"], {\[FormalX], -10 \[Lambda], 10 \[Lambda]}, {\[FormalY], -10 \[Lambda], 10 \[Lambda]}, PlotRange -> All, ColorFunction -> "Rainbow", PlotPoints -> 40]
Out[29]=

Possible Issues

The arguments supplied to the phase and coherence functions are given in micrometers, regardless of the units of the input point array, which can result in arithmetic errors:

In[30]:=
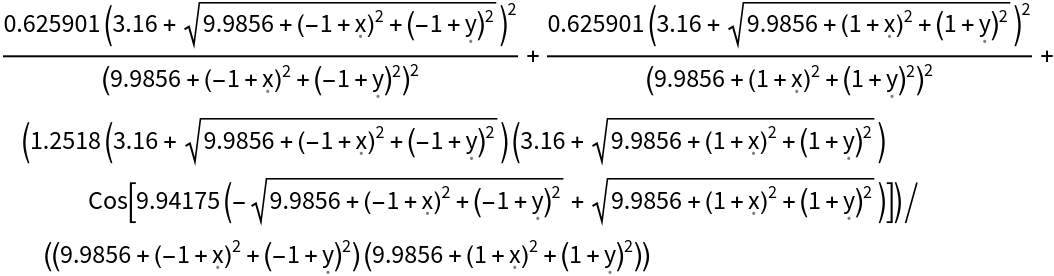
\[Sigma] = 20; ResourceFunction["OpticalFieldModeling"][ QuantityArray[RandomReal[3, {5, 2}], "Millimeters"], "CoherenceFunction" -> (Exp[-((#1^2 + #2^2)/(2 \[Sigma]^2))] &)]
Out[27]=

Resource History

  • Date Created: 16 July 2020

Source Metadata

  • Citation:
    • R. Castañeda, J. Laverde, and J. Moreno. Matrix algorithm for 3D nonparaxial optical field modeling under arbitrary spatial coherence. Appl. Opt. 59: D21- D30 (2020).
    • R. Castañeda, J. Moreno, D. Colorado, J. Laverde. 3D non-paraxial kernel for two-point correlation modelling in optical and quantum interference at the micro and nano-scales. Phys. Scr. 95: 065502 (15pp) (2020).
    • R. Castañeda. Electromagnetic wave fields in the microdiffraction domain. Phys. Rev. A 89: 013843 (14pp) (2014).
    • L. Mandel and E. Wolf, Optical Coherence and Quantum Optics (Cambridge: Cambridge University, 1995).

License Information