Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NumericalMethodFindRoot

Source Notebook

Find the root of an equation or number using a specified numerical method

Contributed by: Jason Martinez

ResourceFunction["NumericalMethodFindRoot"][f,x,method]

searches for a numerical root of f as a function of x, using the specified method.

ResourceFunction["NumericalMethodFindRoot"][f,{x,x0}, method]

searches for a numerical root of f, starting from the point x=x0.

ResourceFunction["NumericalMethodFindRoot"][f,{x,x0},method,property]

returns the specified property for the numerical search.

Details and Options

ResourceFunction["NumericalMethodFindRoot"] supports "Bisection", "Newton" and "Secant" methods.
ResourceFunction["NumericalMethodFindRoot"] has attribute HoldAll.
By default, ResourceFunction["NumericalMethodFindRoot"] returns a list of replacements for x.
ResourceFunction["NumericalMethodFindRoot"] uses the same options as FindRoot, though these are disregarded by the "Bisection" method, which overrides settings for Method.
ResourceFunction["NumericalMethodFindRoot"] supports two values for the property directive:
"Solution"return the root of f
"Steps"return a table of steps taken to reach the root
"PropertyAssociation" can be used as a fourth argument to return an Association of the properties.

Examples

Basic Examples (3) 

Find the root of using Newton’s method:

In[1]:=
ResourceFunction["NumericalMethodFindRoot"][x Cos[x], x, "Newton"]
Out[1]=

Specify a starting point:

In[2]:=
ResourceFunction["NumericalMethodFindRoot"][ x Cos[x], {x, 2}, "Newton"]
Out[2]=

Examine step information:

In[3]:=
grid = ResourceFunction["NumericalMethodFindRoot"][x Cos[x], {x, 2}, "Newton", "Steps"]
Out[3]=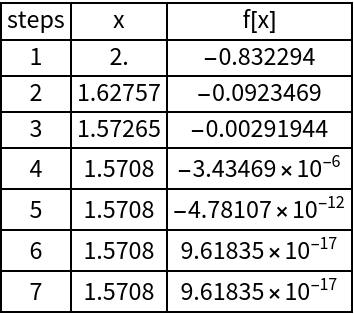

The raw data comprising the grid can be returned by applying Normal:

In[4]:=
Normal@grid
Out[4]=

Scope (2) 

Find a root using the secant method:

In[5]:=
ResourceFunction["NumericalMethodFindRoot"][x^2 - 2, x, "Secant"]
Out[5]=

Determine the steps to locating the root:

In[6]:=
ResourceFunction["NumericalMethodFindRoot"][ x^2 - 2, x, "Secant", "Steps"]
Out[7]=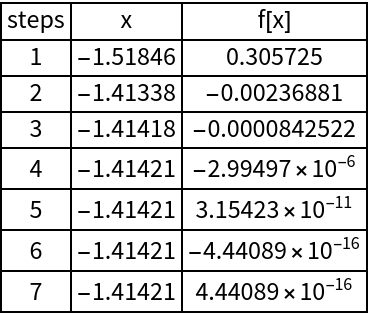

Use complex starting points:

In[8]:=
ResourceFunction["NumericalMethodFindRoot"][ x^5 - 2 == 0, {x, 2 I}, "Newton"]
Out[8]=

Options (1) 

Get higher precision results by increasing WorkingPrecision:

In[9]:=
ResourceFunction["NumericalMethodFindRoot"][ x Cos[x], {x, 2}, "Newton", WorkingPrecision -> 50]
Out[9]=

Version History

  • 1.0.0 – 11 November 2019

Related Resources

License Information