Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NumericalIntegralApproximation

Source Notebook

Determine the value of an integral using a numerical method

Contributed by: Jason Martinez

ResourceFunction["NumericalIntegralApproximation"][f,{x,xmin,xmax},method]

gives a numerical approximation to the integral using the specified method.

Details and Options

ResourceFunction["NumericalIntegralApproximation"] supports the following methods:
"Midpoint"midpoint rule
"RightHand"right Riemann sum
"LeftHand"left Riemann sum
"Simpson"Simpson's rule
"Trapezoidal"trapezoidal rule
"Boole"Boole's rule
"LeftHand", "Midpoint" and "RightHand" methods disregard all option settings except "Intervals".
ResourceFunction["NumericalIntegralApproximation"] takes the following options:
"Intervals"Automaticthe number of subintervals to divide the integral into
WorkingPrecisionMachinePrecisionthe precision used in internal computations
By default, "Intervals" takes the value Automatic, corresponding to a single interval.

Examples

Basic Examples (2) 

Integrate expressions using classic numerical methods such as Simpson’s rule:

In[1]:=
ResourceFunction["NumericalIntegralApproximation"][ x^2 + Sqrt[x], {x, 1, 5}, "Simpson"]
Out[1]=

Compare left hand, right hand, and midpoint integrations:

In[2]:=
ResourceFunction["NumericalIntegralApproximation"][ Sin[Sin[x]], {x, 0, 2}, "LeftHand"]
Out[2]=
In[3]:=
ResourceFunction["NumericalIntegralApproximation"][ Sin[Sin[x]], {x, 0, 2}, "RightHand"]
Out[3]=
In[4]:=
ResourceFunction["NumericalIntegralApproximation"][ Sin[Sin[x]], {x, 0, 2}, "Midpoint"]
Out[4]=

Scope (1) 

Compute integrals with "Trapezoidal" or "Boole" rules:

In[5]:=
ResourceFunction[ "NumericalIntegralApproximation"][(x^2 - 2)/x, {x, 1, 2}, "Trapezoidal"]
Out[5]=
In[6]:=
ResourceFunction[ "NumericalIntegralApproximation"][(x^2 - 2)/x, {x, 1, 2}, "Boole"]
Out[6]=

Options (1) 

Increase accuracy by using multiple intervals:

In[7]:=
ResourceFunction["NumericalIntegralApproximation"][ x^3 - x^2, {x, 1, 3}, "LeftHand", "Intervals" -> 10]
Out[7]=

Applications (2) 

Examine how increasing the number of intervals affects the result:

In[8]:=
results = Table[ResourceFunction["NumericalIntegralApproximation"][ x^3 - x^2, {x, 1, 3}, "Midpoint", "Intervals" -> i], {i, 50}];
In[9]:=
ListPlot[results]
Out[9]=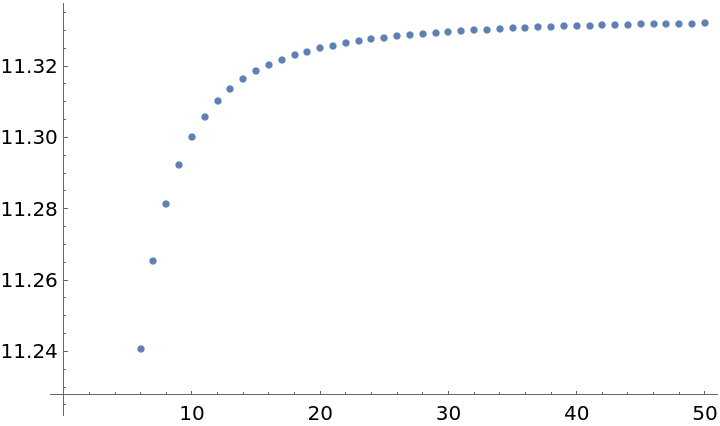

Compare the results to the exact answer:

In[10]:=
Integrate[x^3 - x^2, {x, 1, 3}]
Out[10]=
In[11]:=
N[%]
Out[11]=

Version History

  • 2.0.0 – 09 August 2022
  • 1.0.0 – 08 November 2019

Related Resources

License Information