Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NumPyCholeskyDecomposition

Source Notebook

Compute the Cholesky decomposition of an array in Python using the NumPy linear algebra package

Contributed by: Wolfram Staff

ResourceFunction["NumPyCholeskyDecomposition"][array]

computes the Cholesky decomposition of an array in Python using the package NumPy.

ResourceFunction["NumPyCholeskyDecomposition"][array,session]

uses the specified running ExternalSessionObject session.

Details and Options

ResourceFunction["NumPyCholeskyDecomposition"] is a wrapper function that calls the Python function numpy.linalg.cholesky().
array must be a numeric Hermitian positive definite matrix or a tensor object representing a list of such matrices.
For a matrix array, ResourceFunction["NumPyCholeskyDecomposition"][array] yields an upper or lower-triangular matrix l such that l.ConjugateTranspose[l]==array.
For a real matrix array, ConjugateTranspose[array] can be replaced with Transpose[array].
ResourceFunction["NumPyCholeskyDecomposition"] accepts array in the form of a NumericArray object or an expression that can be converted to NumericArray.
ResourceFunction["NumPyCholeskyDecomposition"][array,session] avoids the overhead of opening a new Python session for every successive call.

Examples

Basic Examples (3) 

Compute the Cholesky decomposition of a symmetric positive-definite matrix in NumPy:

In[1]:=
m = {{2, 1}, {1, 2}};
In[2]:=
ResourceFunction["NumPyCholeskyDecomposition"][m]
Out[2]=
In[3]:=
Normal[%] // MatrixForm
Out[3]=

The original matrix:

In[4]:=
%.Transpose[%]
Out[4]=

In contrast, CholeskyDecomposition always returns an upper-triangular matrix:

In[5]:=
CholeskyDecomposition[m] // N // MatrixForm
Out[5]=
In[6]:=
Transpose[%].%
Out[6]=

Scope (6) 

Compute the Cholesky decomposition of a real-valued matrix:

In[7]:=
m = #.Transpose[#] + IdentityMatrix[4] &@RandomReal[1, {4, 4}]
Out[7]=
In[8]:=
ResourceFunction["NumPyCholeskyDecomposition"][m]
Out[8]=
In[9]:=
MatrixForm[Normal[%]]
Out[9]=
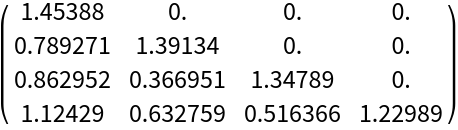
In[10]:=
%.Transpose[%] - m // Chop
Out[10]=

Complex matrix:

In[11]:=
m = #.ConjugateTranspose[#] + IdentityMatrix[4] &@ RandomComplex[1 + I, {4, 4}]
Out[11]=
In[12]:=
ResourceFunction["NumPyCholeskyDecomposition"][m]
Out[12]=
In[13]:=
MatrixForm[Normal[%]]
Out[13]=
In[14]:=
%.ConjugateTranspose[%] - m // Chop
Out[14]=

Sparse array:

In[15]:=
m = Block[{n = 500}, SparseArray[{{i_, i_} -> 2. n^2 - 1., {i_, j_} /; Abs[i - j] == 1 -> -1. n^2}, {n, n}]]
Out[15]=
In[16]:=
ResourceFunction["NumPyCholeskyDecomposition"][%]
Out[16]=
In[17]:=
Normal[%.Transpose[%]] - m // Chop // Flatten // Union
Out[17]=

NumericArray object:

In[18]:=
ResourceFunction["NumPyCholeskyDecomposition"][ NumericArray[#.ConjugateTranspose[#] + IdentityMatrix[4] &@ RandomComplex[1 + I, {4, 4}], "ComplexReal64"]]
Out[18]=

A tensor representing a list of matrices:

In[19]:=
t = #.ConjugateTranspose[#] + IdentityMatrix[4] & /@ RandomComplex[1 + I, {3, 4, 4}]
Out[19]=
In[20]:=
ResourceFunction["NumPyCholeskyDecomposition"][t]
Out[20]=
In[21]:=
Chop[#.ConjugateTranspose[#] & /@ Normal[%] - t]
Out[21]=

Make several calls to NumPyCholeskyDecomposition in the same external session:

In[22]:=
session = StartExternalSession["Python"]
Out[22]=
In[23]:=
ResourceFunction["NumPyCholeskyDecomposition"][ HilbertMatrix[4], session]
Out[23]=
In[24]:=
ResourceFunction["NumPyCholeskyDecomposition"][ HilbertMatrix[5], session]
Out[24]=

End the session:

In[25]:=
DeleteObject[session]

Possible Issues (1) 

NumPyCholeskyDecomposition returns a Failure object if the input matrix is not positive definite:

In[26]:=
RandomComplex[1 + I, {4, 4}]
Out[26]=
In[27]:=
ResourceFunction["NumPyCholeskyDecomposition"][%]
Out[27]=

Version History

  • 1.0.0 – 07 December 2020

License Information