Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the nullity of a matrix
ResourceFunction["Nullity"][mat] computes the nullity of the matrix mat. |
Compute the nullity of a matrix:
| In[1]:= |
| Out[1]= |
Compute the nullity of another matrix:
| In[2]:= |
| Out[2]= |
Compute the nullity of another matrix:
| In[3]:= |
| Out[3]= |
The rank-nullity theorem states that the rank of a matrix plus its nullity equals its column count:
| In[4]:= | ![Grid[Prepend[{MatrixForm[#], MatrixRank[#], ResourceFunction["Nullity"][#], Last[Dimensions[#]]} & /@ {{{1, 2}, {3, 4}}, {{1, 2}, {2, 4}}, {{0, 0}, {0, 0}}, {{1, 2}, {3, 4}, {5, 6}}, {{1, 2, 5}, {2,
4, 6}}, {{1, 2, 3}, {2, 4, 6}, {9, 8, 7}}}
,
{m, MatrixRank[m], ResourceFunction["Nullity"][m], "number of columns"}
], Frame -> All, Background -> {Automatic, {LightBlue, Automatic}}]](https://www.wolframcloud.com/obj/resourcesystem/images/5c5/5c508dd2-693b-40f6-8f59-06c8f05e7a13/0344c4a1674d82df.png) |
| Out[4]= | 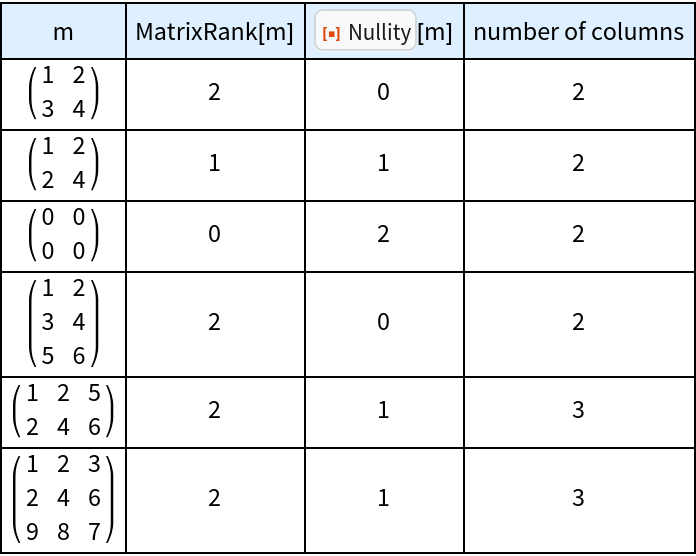 |
When called with symbolic arguments, Nullity assumes maximal linear independence:
| In[5]:= |
| Out[5]= |
The nullity of an identity matrix is always zero:
| In[6]:= |
| Out[6]= |
The nullity of a Hilbert matrix is always zero:
| In[7]:= |
| Out[7]= |
The nullity of a Toeplitz matrix is always zero:
| In[8]:= |
| Out[8]= |
This work is licensed under a Creative Commons Attribution 4.0 International License