Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NthDigit

Source Notebook

Compute the digit in a given place of the positional representation of a number

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["NthDigit"][x,n]

returns the nth base-10 digit of x.

ResourceFunction["NthDigit"][x,n,base]

returns the nth digit of x in the specified base.

Details

ResourceFunction["NthDigit"][x,n] returns the nth most significant digit of x when expressed in standard positional form, padding with zeros to the right of the decimal if necessary.
For numbers x<1, ResourceFunction["NthDigit"][x,1] gives 0 and ResourceFunction["NthDigit"][x,n] gives the digit n-1 places to the right of the decimal point.
If n is larger than Precision[x]/Log[10,b], then ResourceFunction["NthDigit"][x,n,b] returns Indeterminate.
The base b in ResourceFunction["NthDigit"][x,n,b] need not be an integer. For any real b such that b > 1, ResourceFunction["NthDigit"][x,n,b] finds the largest integer multiples of bn that can be subtracted from x while leaving a non-negative remainder.
ResourceFunction["NthDigit"][x,n,b] discards the sign of b.

Examples

Basic Examples (4) 

Compute the nth digit of a given number:

In[1]:=
ResourceFunction["NthDigit"][123.45, 4]
Out[1]=

Give the 2500th digit of π in base 10:

In[2]:=
ResourceFunction["NthDigit"][Pi, 2500]
Out[2]=

Compute the base-10 digits of a number less than 1:

In[3]:=
ResourceFunction["NthDigit"][0.012345, #] & /@ Range[10]
Out[3]=

Give the first 10 digits of 19/7 in base 3:

In[4]:=
ResourceFunction["NthDigit"][19/7, #, 3] & /@ Range[10]
Out[4]=

Scope (3) 

Noninteger bases are allowed:

In[5]:=
ResourceFunction["NthDigit"][Pi, 9, 3 GoldenRatio]
Out[5]=

Compute the number of 1s in the first 10^4 binary digits of π:

In[6]:=
Count[ResourceFunction["NthDigit"][Pi, #, 2] & /@ Range[10^4], 1]
Out[6]=

Plot the distribution of first 10,000 digits of π in base 47:

In[7]:=
ListPlot[BinCounts[ ResourceFunction["NthDigit"][Pi, #, 47] & /@ Range[10000], {0, 46}], DataRange -> {0, 46}]
Out[7]=

Properties and Relations (2) 

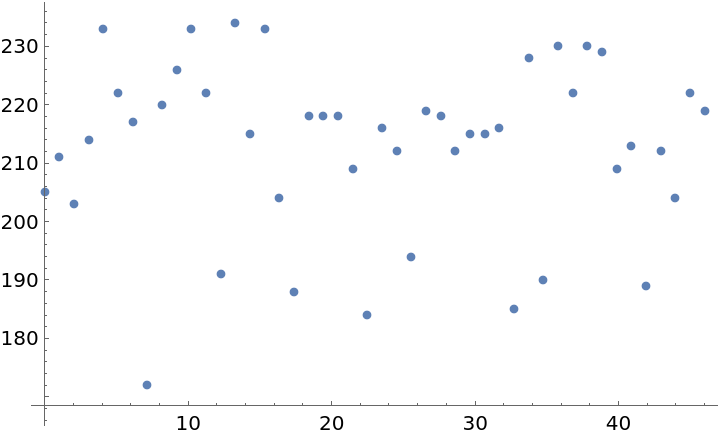NthDigit ignores the sign of its first argument:

In[8]:=
ResourceFunction["NthDigit"][-Sqrt[2], 1]
Out[8]=

NthDigit gives Indeterminate if more digits than the precision are requested:

In[9]:=
ResourceFunction["NthDigit"][5.635`10, 20]
Out[9]=
In[10]:=
ResourceFunction["NthDigit"][5.635`100, 20]
Out[10]=

Possible Issues (1) 

Positional representations only work for bases greater than 1. Using an unsuitable base triggers a message:

Out[10]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 3.0.0 – 23 March 2023
  • 2.1.0 – 05 August 2021
  • 2.0.0 – 06 September 2019
  • 1.0.0 – 31 January 2019

Related Resources

License Information