Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NormalLaplaceDistribution

Source Notebook

A statistical distribution for the sum of a normal and an asymmetric Laplace random variable

Contributed by: Robert Rimmer

ResourceFunction["NormalLaplaceDistribution"][α,β,μ,σ]

represents a normal Laplace distribution.

Details

ResourceFunction["NormalLaplaceDistribution"] results from the sum of a normal random variable and an asymmetric Laplace random variable.
The normal part of this distributation has mean μ and standard deviation σ, and this is added to the difference of exponential distributions with parameters α and β respectively.
This distribution is an auxilliary distribution for the DoubleParetoLogNormalDistribution.

Examples

Basic Examples (2) 

Define and compute the mean of a normal Laplace distribution:

In[1]:=
dist = ResourceFunction["NormalLaplaceDistribution"][0.5, 2.5, 1, 2]; Mean[dist]
Out[2]=

Generate a random sample and fit it to the NormalLaplaceDistribution:

In[3]:=
{a, b, d, c} = {0.5, 2, 3, 2}; s = RandomVariate[ ResourceFunction["NormalLaplaceDistribution"][a, b, d, c], 10000]; h0 = Histogram[s, Automatic, "PDF"]; g1 = Plot[ PDF[ResourceFunction["NormalLaplaceDistribution"][a, b, d, c], x], {x, Min[s], Max[s]}, PlotRange -> All, PlotStyle -> {Thick, Darker[Red]}]; Show[h0, g1]
Out[4]=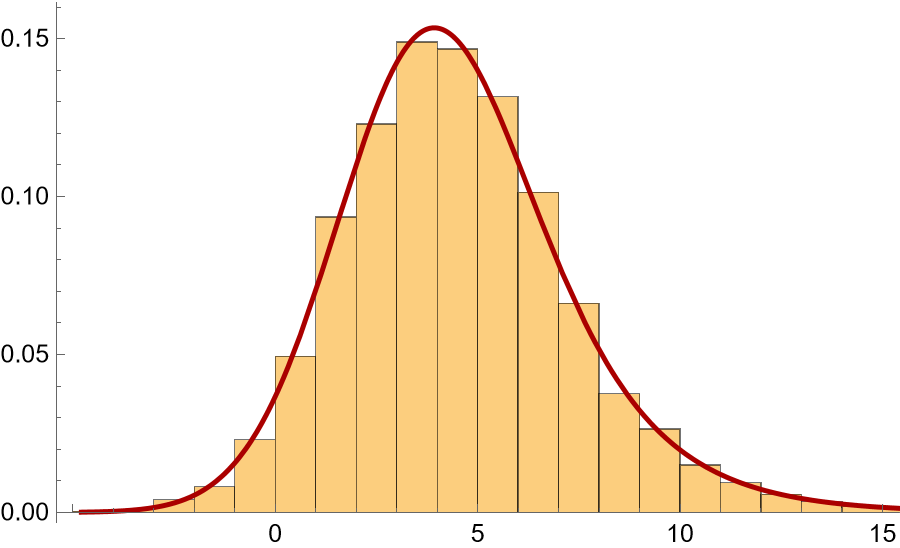

Estimate the distribution from this sample:

In[5]:=
EstimatedDistribution[s, ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]]]
Out[5]=

Display the distribution parameters:

In[6]:=
FindDistributionParameters[s, ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]]]
Out[6]=

Scope (2) 

The distribution can be used with other statistical functions, for example estimate the mean with parameters:

In[7]:=
Mean[ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]]]
Out[7]=

StandardDeviation estimate with parameters:

In[8]:=
StandardDeviation[ ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]]]
Out[8]=

The characteristic function of the NormalLaplaceDistribution:

In[9]:=
CharacteristicFunction[ ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]], t]
Out[9]=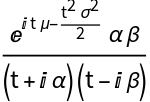

Plot the distribution function for a given set of parameter values:

In[10]:=
Plot[CDF[ResourceFunction["NormalLaplaceDistribution"][1.5, 4, 0, 1], x], {x, -5, 5}]
Out[10]=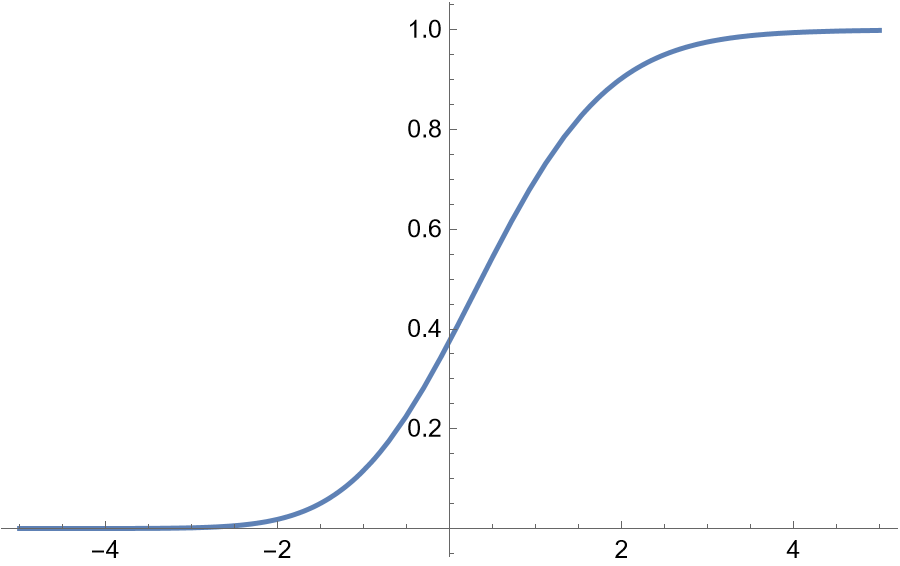

The Quantile function is listable:

In[11]:=
Quantile[ ResourceFunction["NormalLaplaceDistribution"][1.5, 4, 0, 1], {0.25, 0.5, 0.75}]
Out[11]=

The CDF is also listable:

In[12]:=
CDF[ResourceFunction["NormalLaplaceDistribution"][1.5, 4, 0, 1], {0.25, 0.5, 0.75}]
Out[12]=

Properties and Relations (5) 

The NormalLaplaceDistribution is the distribution of the sum of random variables from a NormalDistribution and the difference of two ExponentialDistribution random variables. Start with the TransformedDistribution:

In[13]:=
nlp = TransformedDistribution[ x - y + z, {x \[Distributed] ExponentialDistribution[\[Alpha]], y \[Distributed] ExponentialDistribution[\[Beta]], z \[Distributed] NormalDistribution[\[Mu], \[Sigma]]}]
Out[13]=

When the PDF is requested from the output above the full formula for the density is computed:

In[14]:=
pdf = PDF[nlp, x]
Out[14]=

Check equivalence:

In[15]:=
PDF[ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]], x] == pdf // Simplify
Out[15]=

Here the characteristic function of the transformed distribution is computed:

In[16]:=
cf = CharacteristicFunction[nlp, t]
Out[16]=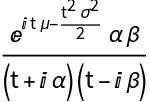

Check equivalence:

In[17]:=
cf == CharacteristicFunction[ ResourceFunction[ "NormalLaplaceDistribution"][\[Alpha], \[Beta], \[Mu], \[Sigma]], t] // Simplify
Out[17]=

Publisher

Robert Rimmer

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 19 August 2024

Source Metadata

  • Citation:
    • This distribution was derived by William Reed. The NormalLaplaceDistribution is used to develop the DoubleParetoLogNormalDistribution. Papers on the distributions and their applications are available at http://www.math.uvic.ca/faculty/reed/
    • This paper describes the distributions and derivation in detail: https://www.math.uvic.ca/faculty/reed/dPlN.3.pdf

License Information