Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Visualize the noise sphere of a set of random numbers
ResourceFunction["NoiseSphere"][{r1,…,rn}] plots Pickover's noise sphere visualization of the numbers ri. |
Noise sphere of the IBM RANDU generator; the structured appearance suggests unwanted correlations:
| In[2]:= |
![ResourceFunction["NoiseSphere"][
BlockRandom[
SeedRandom[1, Method -> {"Congruential", "Multiplier" -> 65539, "Increment" -> 0,
"Modulus" -> 2^31}]; RandomReal[1, 1*^4]]]](https://www.wolframcloud.com/obj/resourcesystem/images/b17/b1763c92-5626-4ed0-bf0b-1127f11bc692/00faf41080e9cc0f.png)
|
| Out[2]= |

|
Noise sphere of a linear congruential generator from L'Ecuyer:
| In[3]:= |
![ResourceFunction["NoiseSphere"][
BlockRandom[
SeedRandom[1, Method -> {"Congruential", "Multiplier" -> 85876534675, "Increment" -> 0, "Modulus" -> 137438953447}]; RandomReal[1, 1*^4]]]](https://www.wolframcloud.com/obj/resourcesystem/images/b17/b1763c92-5626-4ed0-bf0b-1127f11bc692/5b8a74c93b179c60.png)
|
| Out[3]= |

|
Noise sphere of the legacy pseudorandom number generator used by the Wolfram Language:
| In[4]:= |
|
| Out[4]= |

|
The following shows an example of a poor pseudorandom sequence:
| In[5]:= |
|
| Out[5]= |
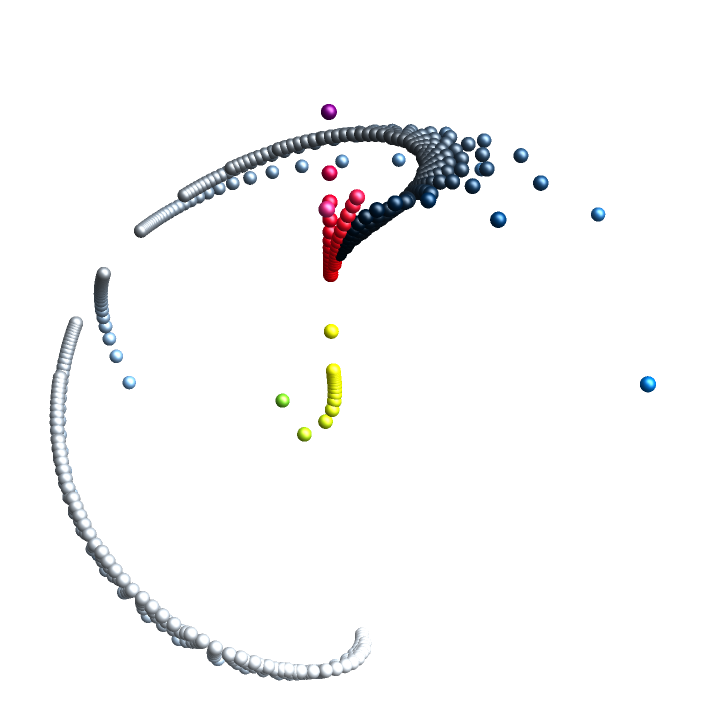
|
This work is licensed under a Creative Commons Attribution 4.0 International License