Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
For each element of a list, find the index of the next greater element
ResourceFunction["NextGreaterElementIndex"][list] for each element of list, find the index of the next numerically greater element. | |
ResourceFunction["NextGreaterElementIndex"][list,p] find the indices using order function p. |
Visualize the input data:
| In[1]:= |
| Out[2]= | 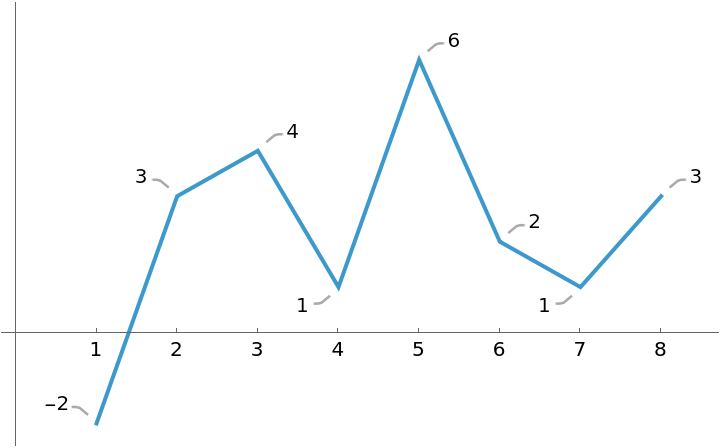 |
The indices of the next greater elements:
| In[3]:= |
| Out[3]= |
Except for columns ending in -1, each second item is the next greater element:
| In[4]:= |
| Out[4]= | 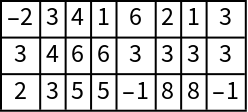 |
For non-numeric input, one may use customized order function:
| In[5]:= |
| Out[6]= |  |
For instance the sixth item in the date list, , is the next later day than :
| In[7]:= |
| Out[7]= |
Comparable Quantity objects are supported:
| In[8]:= | ![SeedRandom["10Units"];
data = MapThread[Quantity[#1, #2] &, {
RandomReal[{1, 5}, 10],
RandomChoice[{"Feet", "Meters", "Kilometers", "Millimeters", "Inches"}, 10]}];](https://www.wolframcloud.com/obj/resourcesystem/images/e2b/e2b5dedd-178e-4278-bdad-647aeaff28e4/4e4ac0c034cd3fc8.png) |
| In[9]:= |
| Out[9]= |
Check the index of each next greater item visually:
| In[10]:= |
| Out[10]= | 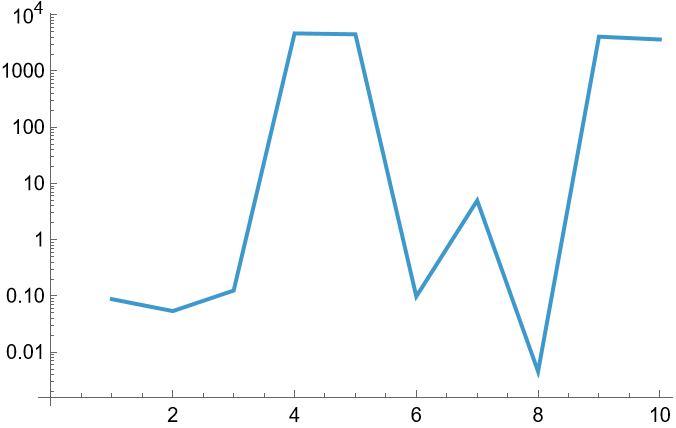 |
Collect and show data for a stock:
| In[11]:= |
| In[12]:= |
| Out[12]= | 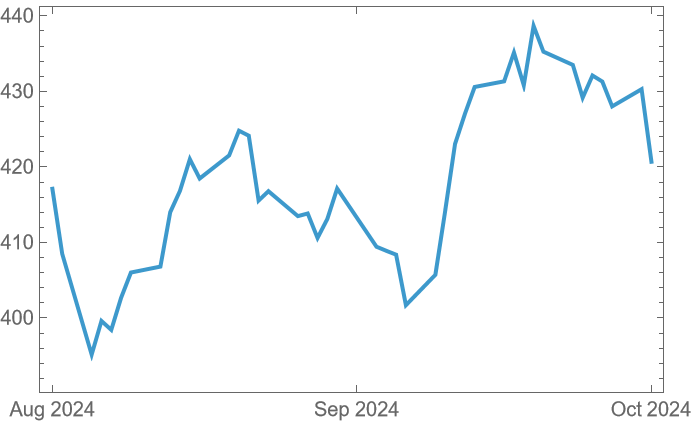 |
Find the wait time to observe an overshoot in stock price for a given duration:
| In[13]:= |
| Out[14]= |
Tabulate the current price and next high:
| In[15]:= | ![ResourceFunction[
ResourceObject[<|"Name" -> "NiceGrid", "ShortName" -> "NiceGrid", "UUID" -> "d46856e8-5702-4b8b-addf-d92743399b5f", "ResourceType" -> "Function", "Version" -> "2.0.0", "Description" -> "Nicely format data in various structures into a grid format", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$8d6838630917472ab156bd9f4b91491e`NiceGrid", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/22e777c3-ca4a-4e8b-a448-bbf28aa4ef3a"]|>, ResourceSystemBase -> Automatic]][MapThread[
{If[# == -1, "Never", QuantityMagnitude@
DateDifference[dp[[#2, 1]], dp[[#1, 1]]]], #3} &,
{idx, Range[Length[idx]], fd["Values"]}
], { "Next Higher price after # day(s)", "Price"}, "MaxNumber" -> 20]](https://www.wolframcloud.com/obj/resourcesystem/images/e2b/e2b5dedd-178e-4278-bdad-647aeaff28e4/52d280fa8aff7881.png) |
| Out[15]= | 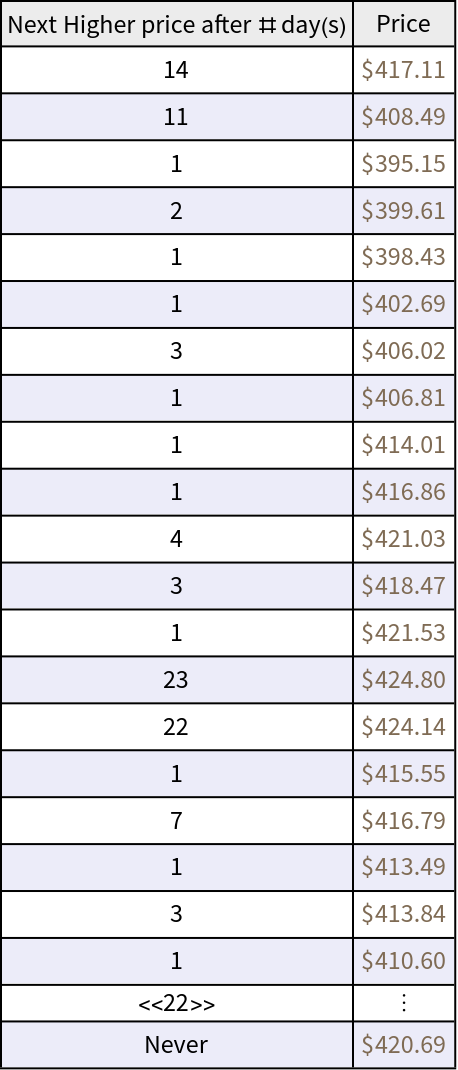 |
An empty input list returns an empty list:
| In[16]:= |
| Out[16]= |
A single element list returns {-1}:
| In[17]:= |
| Out[17]= |
The single argument input must be a list of real valued numeric values. Otherwise the function returns unevaluated:
| In[18]:= |
| Out[18]= |
For non-comparable items, Order is applied automatically:
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License