Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NewtonMethod

Source Notebook

Approximate the root of a function using Newton’s method

Contributed by: Dennis M Schneider

ResourceFunction["NewtonMethod"][f,{x,x0},n]

returns the root approximation obtained by applying Newton’s method at most n times to a differentiable function f with starting value x0.

Examples

Basic Examples (3) 

Use Newton’s method to approximate the root of a function:

In[1]:=
Plot[x Sin[4 x], {x, 0, 3}]
Out[1]=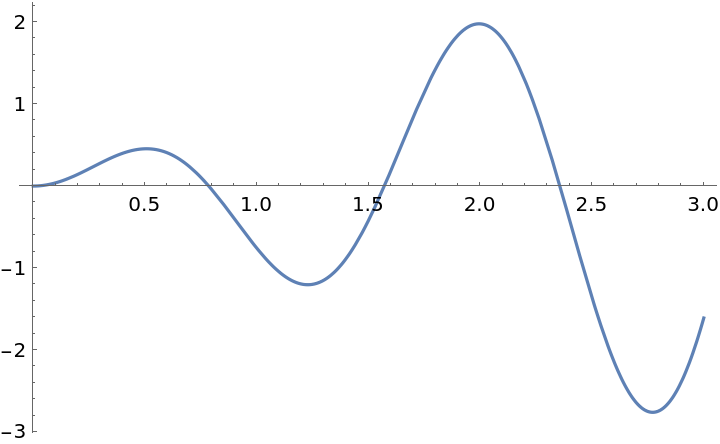

Approximate the root around x=1.5:

In[2]:=
ResourceFunction["NewtonMethod"][x Sin[4 x], {x, 1.5}]
Out[2]=

Show the iterations found:

In[3]:=
ResourceFunction["NewtonMethod"][x Sin[4 x], {x, 1.5}, "PrintDisplay" -> True]
Out[3]=

Scope (2) 

A more complicated function. First, plot it:

In[4]:=
g[x_] := Integrate[Sin[t^2], {t, 0, x}] - 2/3 Plot[g[x], {x, 0, 3}]
Out[5]=

Approximate the root around x=1:

In[6]:=
NMsoln = ResourceFunction["NewtonMethod"][g[x], {x, 1}, 15, "PrintDisplay" -> True, WorkingPrecision -> 20]
Out[6]=

Compare with FindRoot:

In[7]:=
FindRoot[g[x], {x, 1}, WorkingPrecision -> 20]
Out[7]=

Another complicated function:

In[8]:=
ResourceFunction["NewtonMethod"][Tan[x] - x, {x, 4.3}, 15, "PrintDisplay" -> True]
Out[8]=

Compare with FindRoot:

In[9]:=
FindRoot[Tan[x] - x, {x, 4.3}]
Out[9]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 20 August 2019

Related Resources

License Information