Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the companion matrix for the Newton interpolating polynomial of a given set of points
ResourceFunction["NewtonCompanionMatrix"][{f1,f2,…}] yields the Newton companion matrix of an interpolating polynomial which reproduces the function values fi at successive integer values 1, 2, …. | |
ResourceFunction["NewtonCompanionMatrix"][{{x1,f1},{x2,f2},…}] yields the Newton companion matrix of an interpolating polynomial for the function values fi corresponding to the abscissas xi. | |
ResourceFunction["NewtonCompanionMatrix"][{{{x1},f1,df1,…},…}] yields the Newton companion matrix of an interpolating polynomial that reproduces derivatives as well as function values. |
Construct the Newton companion matrix for the squares:
| In[1]:= |
|
| Out[1]= |
|
Check its characteristic polynomial:
| In[2]:= |
|
| Out[2]= |
|
Construct the Newton companion matrix corresponding to an interpolating polynomial through three points:
| In[3]:= |
|
| Out[3]= |
|
The characteristic polynomial is a scalar multiple of the corresponding interpolating polynomial:
| In[4]:= |
|
| Out[4]= |
|
| In[5]:= |
|
| Out[5]= |
|
Newton companion matrix for symbolic points:
| In[6]:= |
|
| Out[6]= |
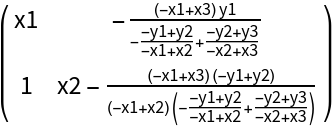
|
Construct the Newton companion matrix for points with derivative information supplied:
| In[7]:= |
|
| Out[7]= |

|
Find the roots of an interpolating polynomial by computing the eigenvalues of a Newton companion matrix:
| In[8]:= |
|
| Out[8]= |
|
Compare with the result of using NSolve:
| In[9]:= |
|
| Out[9]= |
|
The dimensions of a Newton companion matrix might be much less than the number of points supplied:
| In[10]:= |
![pts = {{-1, -4}, {-(2/3), -(107/27)}, {-(1/3), -(118/
27)}, {0, -5}, {1/3, -(152/27)}, {2/3, -(163/27)}, {1, -6}};
ResourceFunction["NewtonCompanionMatrix"][pts] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/7fc/7fc35e73-92dc-45d3-8a73-2843937f49f3/265458a5b751d185.png)
|
| Out[10]= |
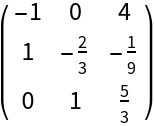
|
| In[11]:= |
|
| Out[11]= |
|
In this case, the corresponding interpolating polynomial has degree 3:
| In[12]:= |
|
| Out[12]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License