Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Iteratively construct graphs up to a termination condition
ResourceFunction["NestWhileGraph"][f,expr,test] generates a directed graph whose nodes are obtained by applying f repeatedly, starting from expr, and continuing until applying test to the result no longer yields True. | |
ResourceFunction["NestWhileGraph"][f,expr,test,m] supplies a list of the most recent m results to test at each step. | |
ResourceFunction["NestWhileGraph"][f,expr,test,All] supplies a list of all results so far to test at each step. | |
ResourceFunction["NestWhileGraph"][f,expr,test,m,max] applies f at most max times. |
Construct a graph by applying f while VertexCount is less than 5:
| In[1]:= |
| Out[1]= |
Apply a similar termination condition only to growth-front subgraph:
| In[2]:= | ![ResourceFunction["NestWhileGraph"][{f[#], g[#]} &, 0, Function[{g1, g2},
VertexCount@VertexDelete[g2, VertexList[g1]]
] @@ # <= 8 &, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/11a26d23a29db98c.png) |
| Out[2]= | 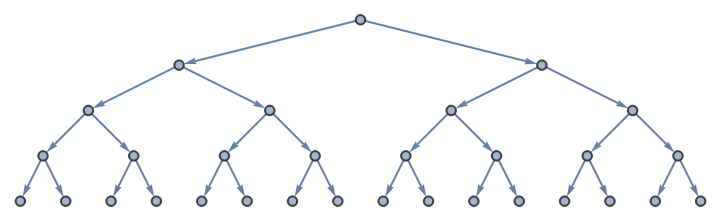 |
Terminate the growth of a graph according to properties of its vertex set:
| In[3]:= | ![ResourceFunction["NestWhileGraph"][{# + 1, 2 # + 1} &, 0,
Function[{g0}, Length[Select[VertexList[g0],
VertexInDegree[g0, #] == 2 &]]][#] < 8 &, 1]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/647d575f42d3928d.png) |
| Out[3]= | 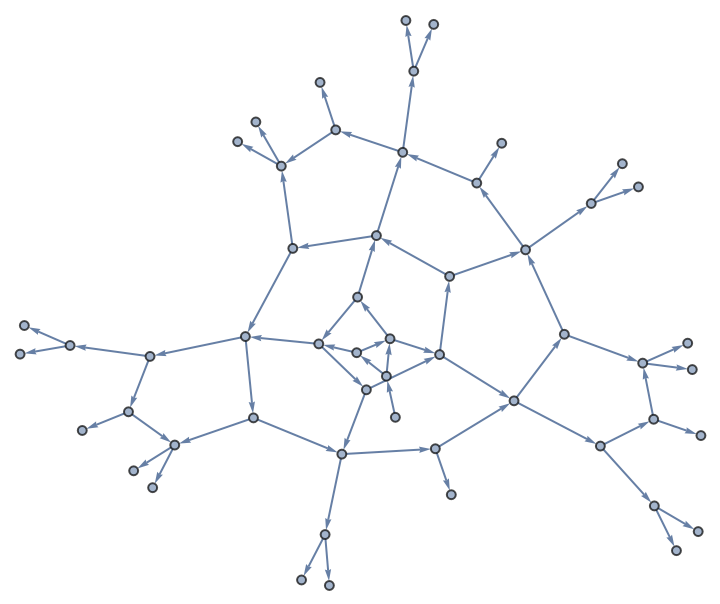 |
Explore a grid graph through multiway spacetime evolution until every vertex has been visited:
| In[4]:= | ![Function[{dim}, Graph3D[#, GraphLayout -> "SpringElectricalEmbedding"] &@
With[{moves = Association[# -> VertexOutComponent[
GridGraph[{dim, dim}], #, {1}] & /@ Range[dim^2]]},
ResourceFunction["NestWhileGraph"][
Thread[{moves[#[[1]]], #[[2]] + 1}] &, {{1, 0}},
UnsameQ[Union[First /@ Flatten[VertexList /@ #, 1]],
Range[dim^2]] &, All ]]][5]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/25ab820ef0c35fb0.png) |
| Out[4]= | 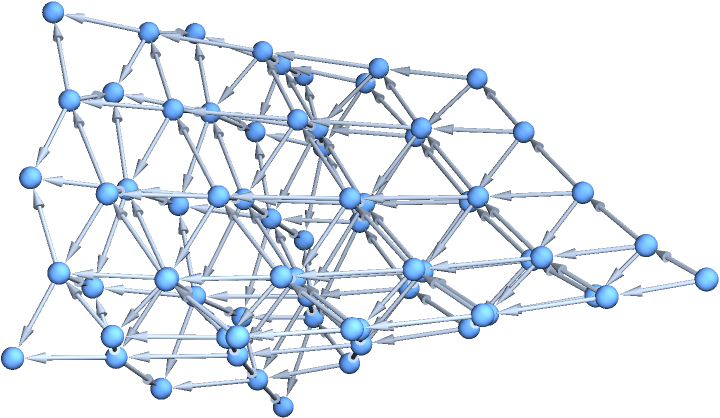 |
Generate a torus graph:
| In[5]:= | ![Function[{n, m}, ResourceFunction["NestWhileGraph"][{
Mod[Plus[#, {1, 0}], {n, m}],
Mod[Plus[#, {0, 1}], {n, m}]} &,
{{0, 0}}, UnsameQ @@ # &, 2]][12, 6]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/6b1641dd9c5e0421.png) |
| Out[5]= | 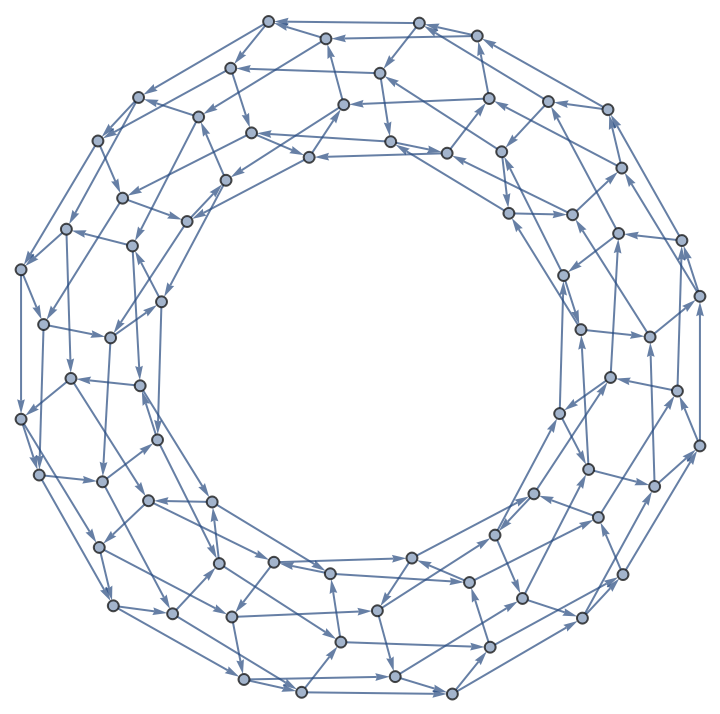 |
Generate a few different Cayley graphs for the Octahedral group:
| In[6]:= | ![Grid[{Function[{cyca, cycb}, Graph3D[ResourceFunction["NestWhileGraph"][{
PermutationProduct[Cycles[{cyca}], #],
PermutationProduct[Cycles[{cycb}], #]} &, Cycles[{{}}],
UnsameQ @@ # &, 2], ImageSize -> 180]][#1, #2] & @@@ {
{{1, 2, 3, 4}, {3, 4}}, {{1, 2, 3}, {3, 4}}, {{1, 2, 3, 4}, {2, 3,
4}}}},
Frame -> All, FrameStyle -> LightGray, Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/284ec9cc788ee7e1.png) |
| Out[6]= | 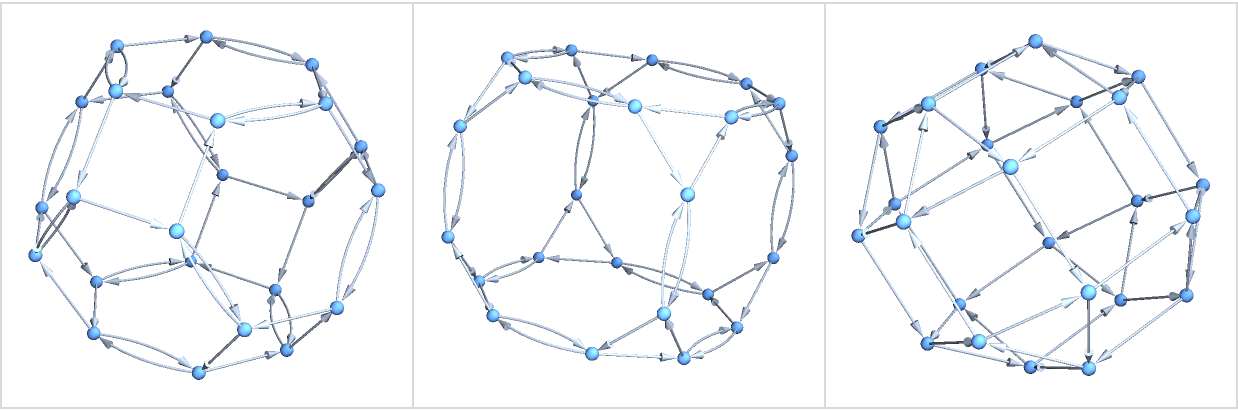 |
Termination can also be accomplished by introducing a cutoff for recursion depth:
| In[8]:= |
| Out[8]= |
Construct the game graph of a loopy game:
| In[9]:= | ![With[{IterateGameState = Function[{board, player},
With[{loc = Position[board, player][[1, 1]]},
Union[Switch[{Total[#[[1]]], #},
{_, {{__, 1}, -1}}, 1,
{_, {{-1, __}, 1}}, -1,
{0, {_, _}}, #,
{1, {_, _}}, ReplacePart[#, {1, -1} -> -1],
{-1, {_, _}}, ReplacePart[#, {1, 1} -> 1]
] & /@ Complement[{ReplacePart[board, If[0 < (loc + player #) < 7,
{loc -> 0, (loc + player #) -> player}, {}]],
-player} & /@ {1, 2},
{{board, -player}}]]]]},
gameGraph = SimpleGraph@
ResourceFunction["NestWhileGraph"][IterateGameState @@ # &,
{{{1, 0, 0, 0, 0, -1}, 1}}, UnsameQ @@ # &, 2,
GraphLayout -> "LayeredDigraphEmbedding"]]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/76b1f4e926b72552.png) |
| Out[9]= | 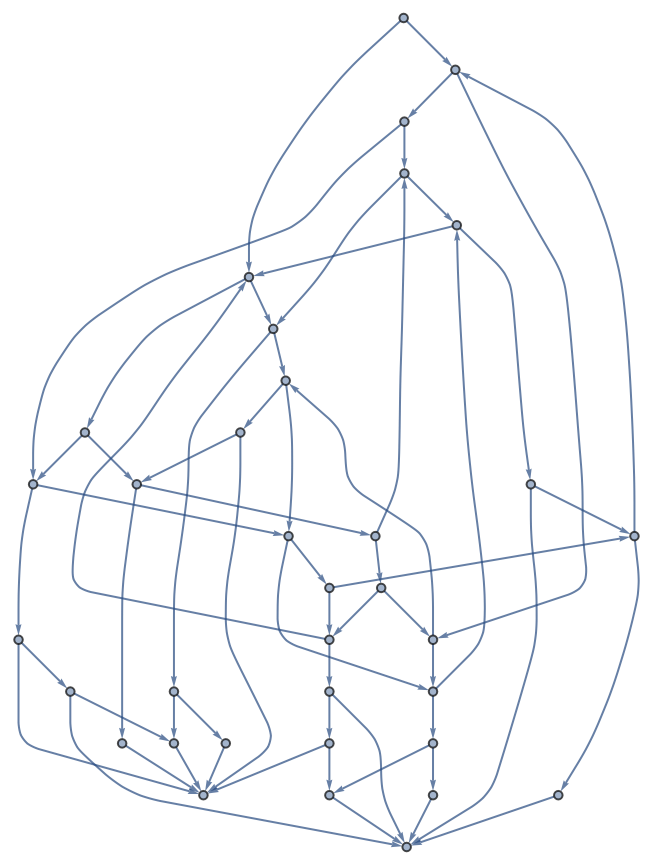 |
Find loops in the game graph:
| In[10]:= | ![Grid[Partition[With[{cycles = FindCycle[gameGraph, Infinity, All]},
HighlightGraph[gameGraph, PathGraph[#], ImageSize -> {40, Automatic}] & /@ cycles], 11],
Frame -> All, FrameStyle -> LightGray, Spacings -> {1, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/14de286ab7271853.png) |
| Out[10]= |  |
Generate a graph with structure related to prime numbers:
| In[11]:= | ![primeg = ResourceFunction["NestWhileGraph"][Function[{val},
Append[val + # & /@ FactorInteger[val][[All, 1]], val + 1]]
, 1, UnsameQ[Length@Intersection[
Prime /@ Range[15], VertexList[#]], 15] &]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/42e8accd2c0f4e7a.png) |
| Out[11]= | 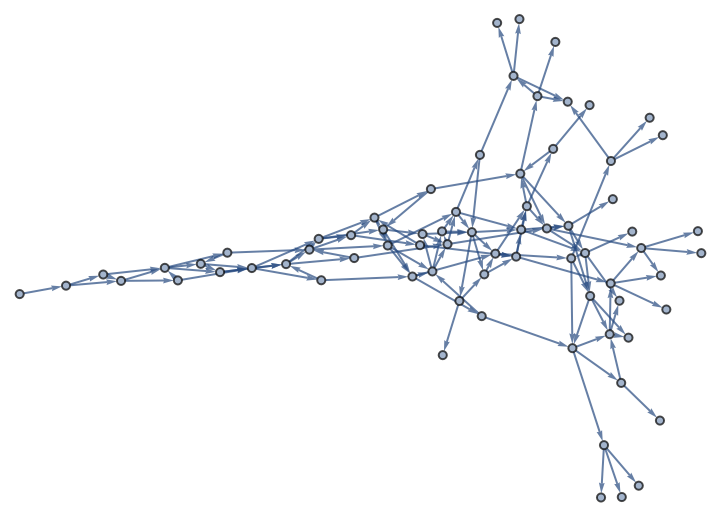 |
Notice false positives on the growth front:
| In[12]:= | ![TableForm[#[Sort@Select[
Sort@VertexList[primeg],
VertexInDegree[primeg, #] == 1 &],
Prime /@ Range[25]
] & /@ {Intersection, Complement}]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e38594-73df-44fc-bcca-d88d8d7aa6b0/0b5e4a9da9dacbe2.png) |
| Out[12]= |
This work is licensed under a Creative Commons Attribution 4.0 International License