Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create a graph by successively applying a function and differently tagging edges corresponding to different outputs
ResourceFunction["NestGraphTagged"][f,expr,n] gives the tagged graph obtained by starting with expr and applying f successively n times. |
| "StateLabeling" | False | whether to render states as boxes |
| "RuleStyling" | Automatic | list of styles for edges/rules |
| "FormattingFunction" | Automatic | how to format a state |
| "PostProcessGraph" | Identity | post-process graph |
Make a nested graph with edge coloring:
| In[1]:= |
| Out[1]= | 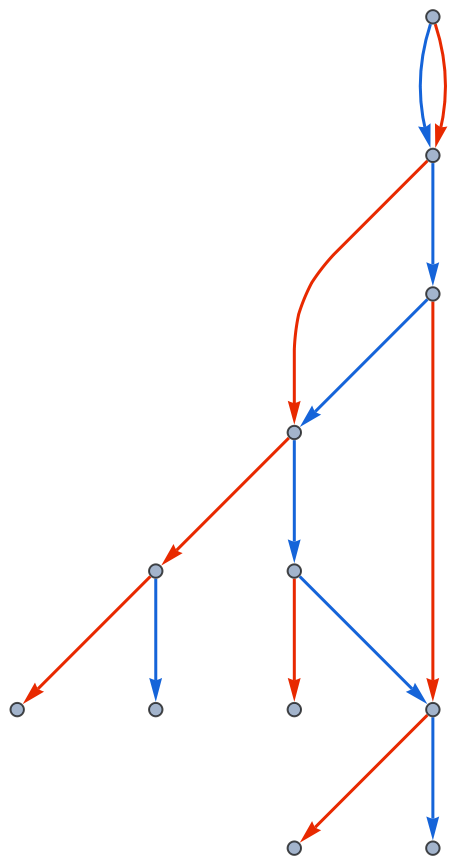 |
Use a pure function:
| In[2]:= |
| Out[2]= | 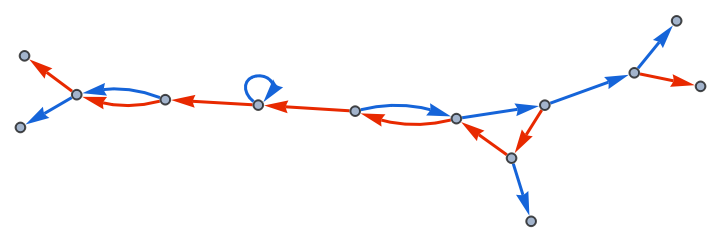 |
Use a list of initial expressions:
| In[3]:= |
| Out[4]= | 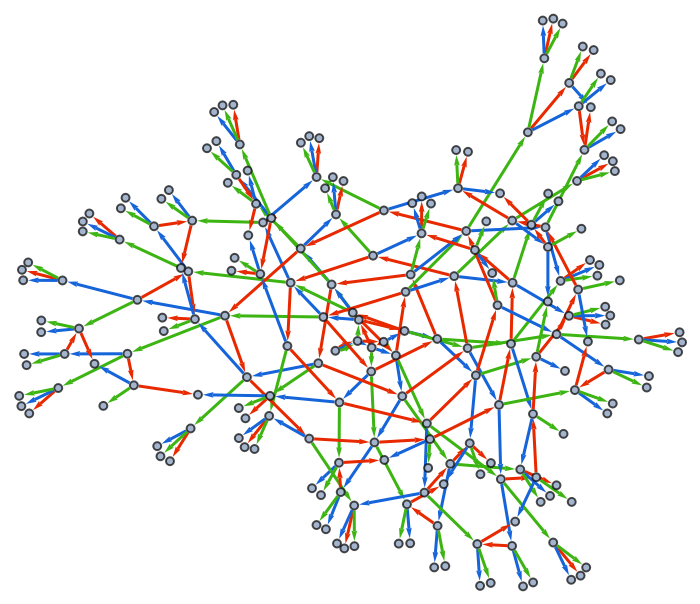 |
Add a legend to explain colors:
| In[5]:= | ![ResourceFunction["NestGraphTagged"][n |-> {2 n, n + 1, n - 1}, {1}, 4,
PlotLegends -> TraditionalForm /@ {2 n, n + 1, n - 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/4c12285a3814252e.png) |
| Out[5]= |  |
Label the vertex states in a nested graph:
| In[6]:= |
| Out[6]= | 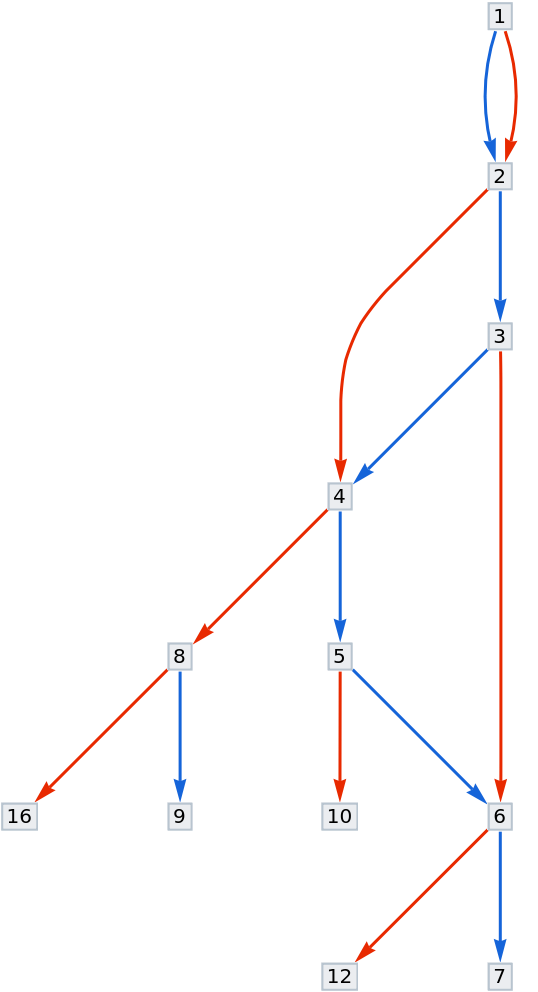 |
Edge colorings can be overridden:
| In[7]:= |
| Out[7]= | 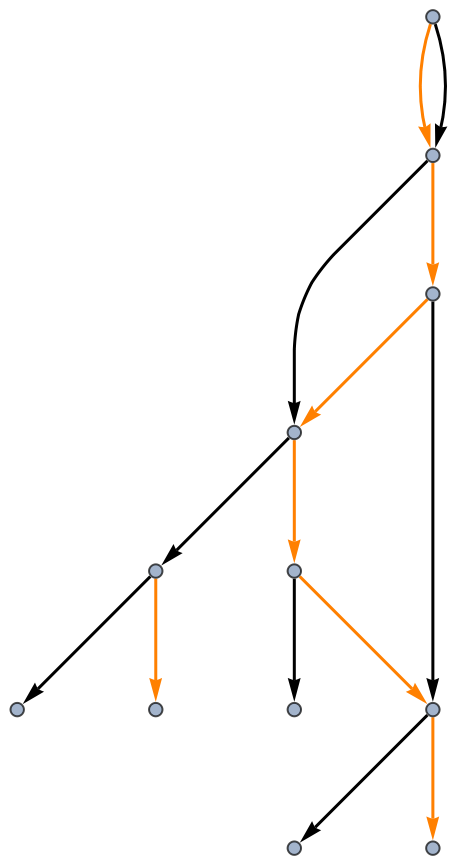 |
Add labels to edges with EdgeLabels and a pattern:
| In[8]:= | ![ResourceFunction["NestGraphTagged"][n |-> {2 n, n + 1}, {1}, 4, EdgeLabels -> {
DirectedEdge[_, _, t_] /; OddQ[t] :> Placed[t, {1/2, {-1, 1/2}}],
DirectedEdge[_, _, t_] /; EvenQ[t] :> Placed[t, {1/2, {1, 1/2}}]}, EdgeLabelStyle -> Directive[12, Bold]]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/19ccd060b010fd6f.png) |
| Out[8]= | 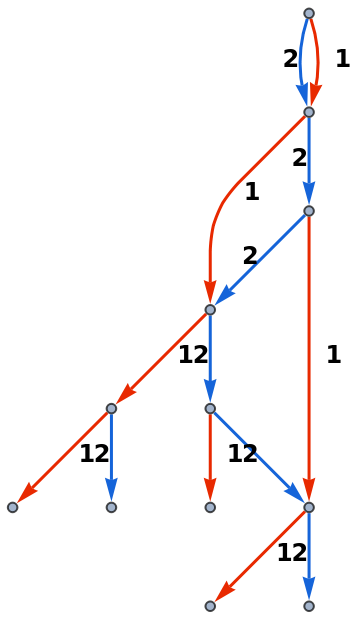 |
Add edge labels using output index:
| In[9]:= | ![ResourceFunction["NestGraphTagged"][n |-> {n + 2, n + 3}, 0, 4, "StateLabeling" -> True, EdgeLabels -> {
1 -> Placed["+2", {.7, {-.2, 0}}], 2 -> Placed["+3", {.7, {-.2, 0}}]
}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/2ffdd35a37d4965e.png) |
| Out[9]= | 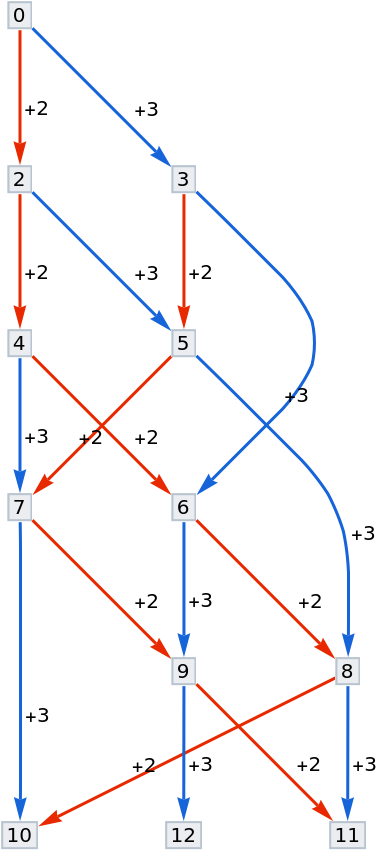 |
Add tooltips to edges:
| In[10]:= |
| Out[10]= | 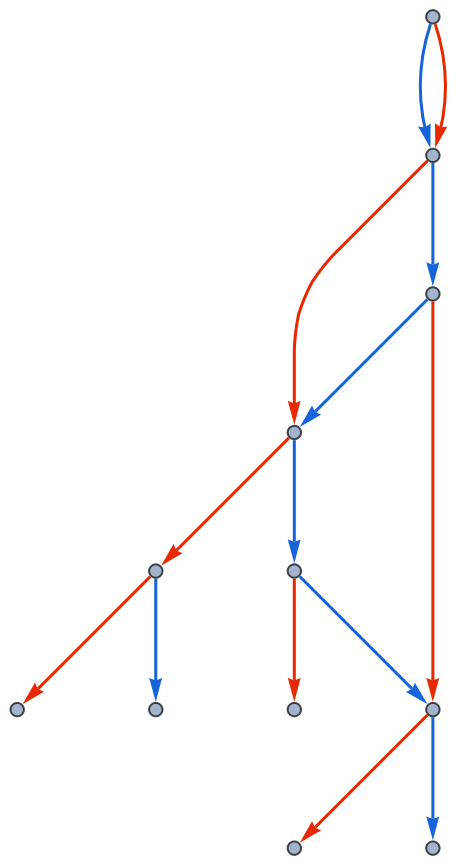 |
Make custom edge tags by returning a list of rules (tags will be pairs of the form {key, index}):
| In[11]:= |
| Out[11]= | 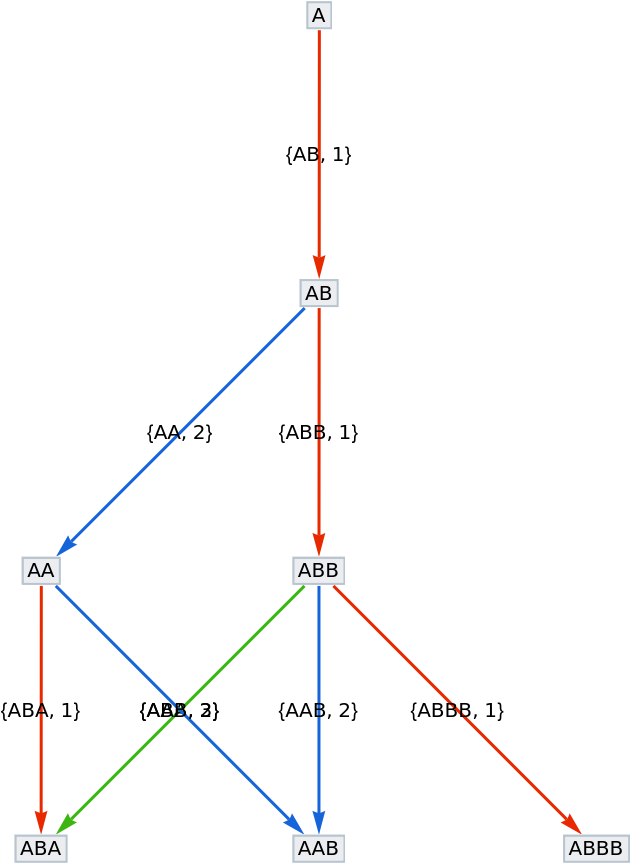 |
Make custom edge tags by returning an association:
| In[12]:= | ![ResourceFunction["NestGraphTagged"][
n |-> <|"\[Times]2" -> 2 n, "+1" -> n + 1|>, 2, 3, "StateLabeling" -> True, EdgeLabels -> "EdgeTag"]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/65bc837117a5b9d5.png) |
| Out[12]= | 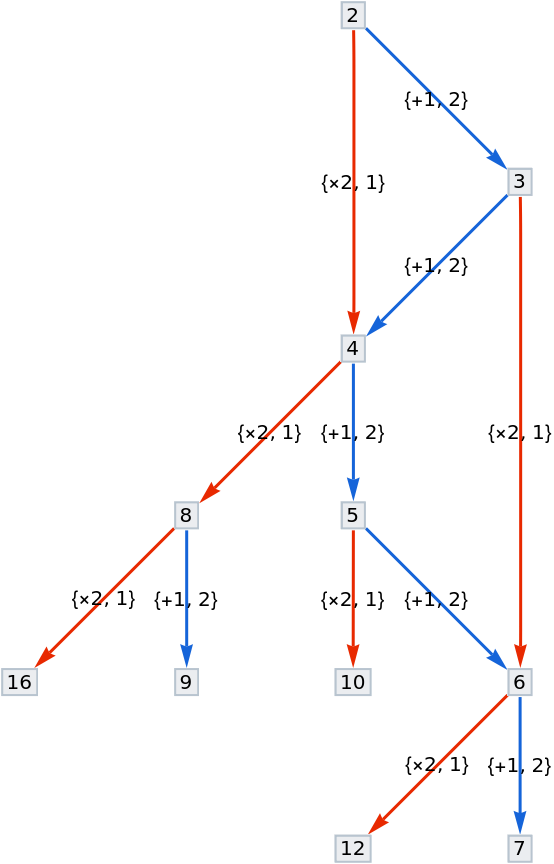 |
Turn on special vertex shapes:
| In[13]:= |
| Out[13]= | 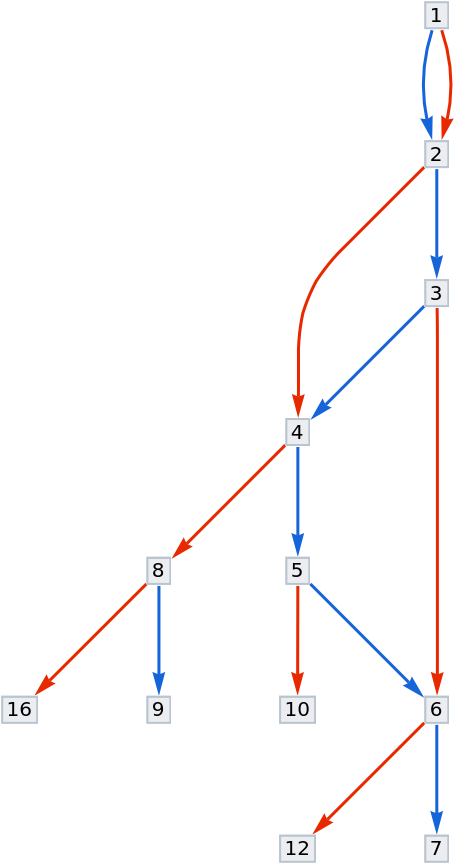 |
Change the formatting for vertex 31:
| In[14]:= | ![ResourceFunction["NestGraphTagged"][
n |-> Mod[{2 n + 1, 3 n + 1}, 144], {1}, 200, "StateLabeling" -> True, "FormattingFunction" -> (# /. {31 -> Style[31, Red, Bold, 16], x_ :> Style[x, Black]} &)]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/2998aa9b4e92a6cf.png) |
| Out[14]= | 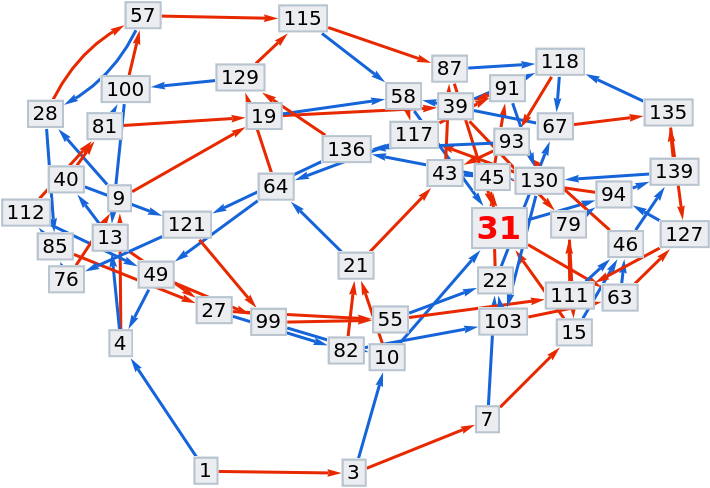 |
Use custom styles for output values:
| In[15]:= |
| Out[15]= | 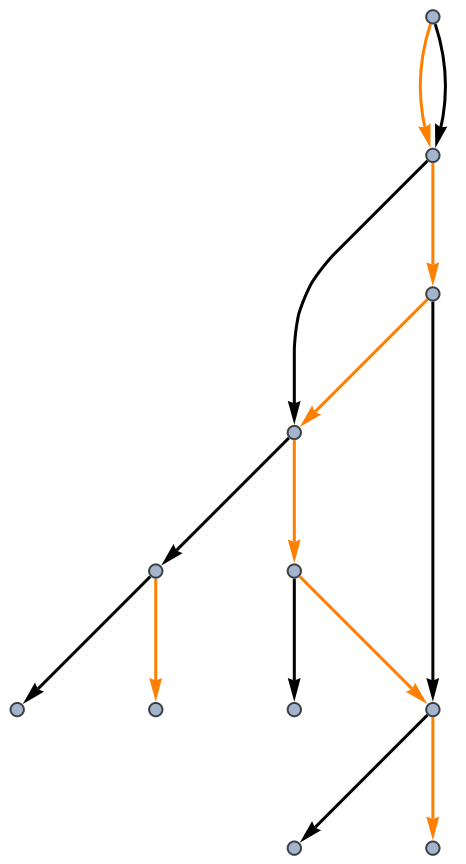 |
If the output is graphics with a legend, it useful to apply some custom function to the graph itself:
| In[16]:= | ![ResourceFunction["NestGraphTagged"][n |-> {2 n, n + 1, n - 1}, {1}, 4,
"PostProcessGraph" -> ReverseGraph, PlotLegends -> TraditionalForm /@ {2 n, n + 1, n - 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/22a5f7fa513dffcf.png) |
| Out[16]= | 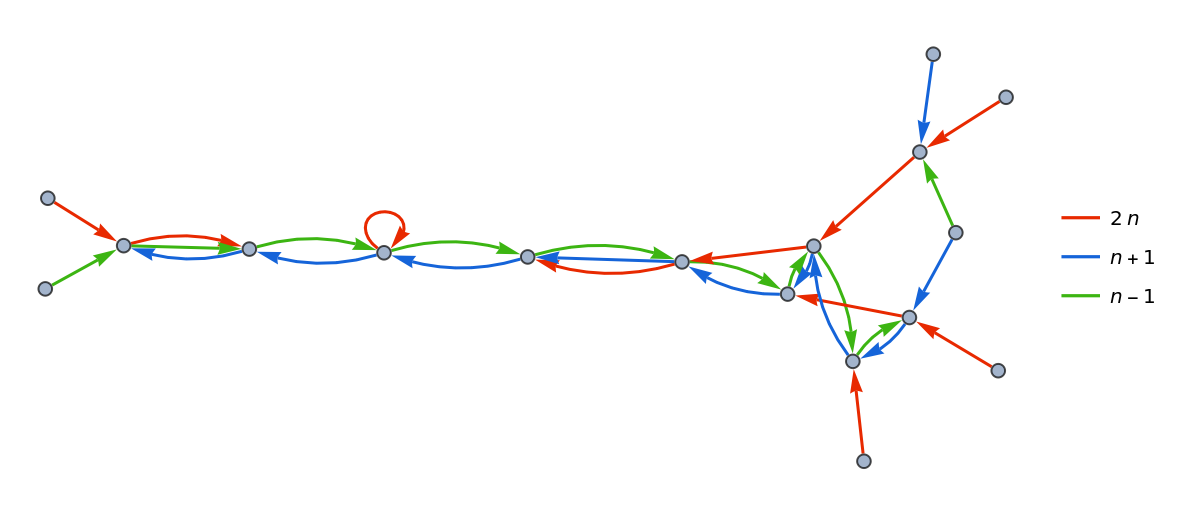 |
Vertices can be number pairs:
| In[17]:= |
| Out[17]= | 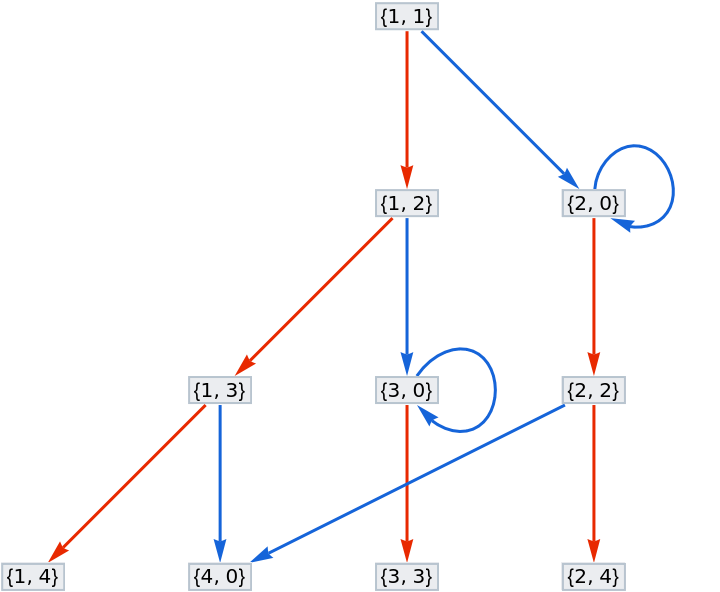 |
For a remainder graph, to find 2143 (mod 7), start at 0 and follow ![]() (2143) to get remainder 1:
(2143) to get remainder 1:
| In[18]:= | ![ResourceFunction["NestGraphTagged"][v |-> Mod[{v + 1, 10 v}, 7], Range[1], 10, "StateLabeling" -> True, GraphLayout -> "CircularEmbedding"]](https://www.wolframcloud.com/obj/resourcesystem/images/bc9/bc9dac5e-7af2-4317-8e0b-693d5ab67bf4/6b431bf973a031c5.png) |
| Out[18]= | 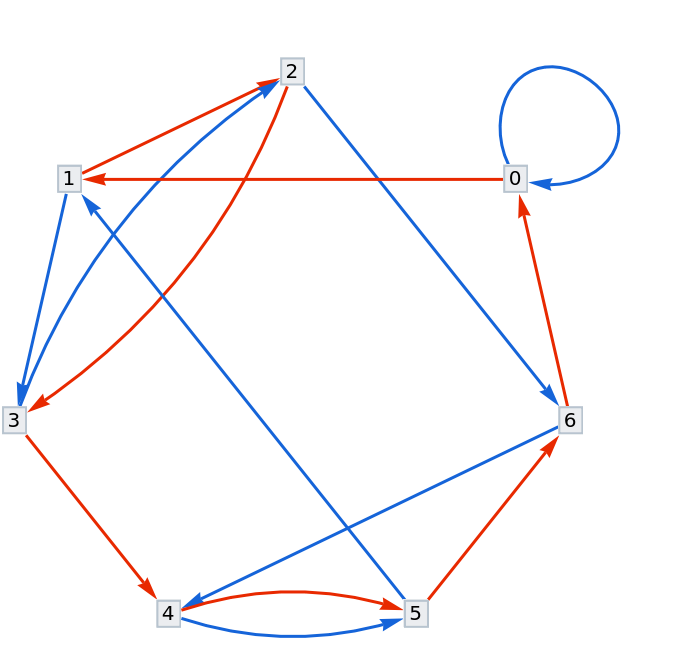 |
This work is licensed under a Creative Commons Attribution 4.0 International License