Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NaturalEquations

Source Notebook

Compute the natural equations of a curve

Contributed by: Wolfram Staff (original content by Eric W. Weisstein)

ResourceFunction["NaturalEquations"][c,t]

computes the natural equations of a curve c with parameter t.

Details and Options

A natural equation is an equation that specifies a curve independent of any choice of coordinates or parametrization.
Natural equations are computed using the tangential angle , where κ is the curvature, s is the arc length, and and are the coordinates.
ResourceFunction["NaturalEquations"] accepts the same options as Integrate.

Examples

Basic Examples (3) 

Natural equations for a circle:

In[1]:=
ResourceFunction["NaturalEquations"][ Entity["PlaneCurve", "Circle"]["ParametricEquations"][a][t], t] // PowerExpand
Out[1]=

Natural equations for several curves:

In[2]:=
{#, ResourceFunction[ "NaturalEquations"][#["ParametricEquations"][a][t], t]} & /@ {Entity["PlaneCurve", "CircleInvolute"], Entity["PlaneCurve", "Cycloid"], Entity["PlaneCurve", "Deltoid"], Entity["PlaneCurve", "Nephroid"], Entity["PlaneCurve", "Cardioid"]} // PowerExpand // Grid
Out[2]=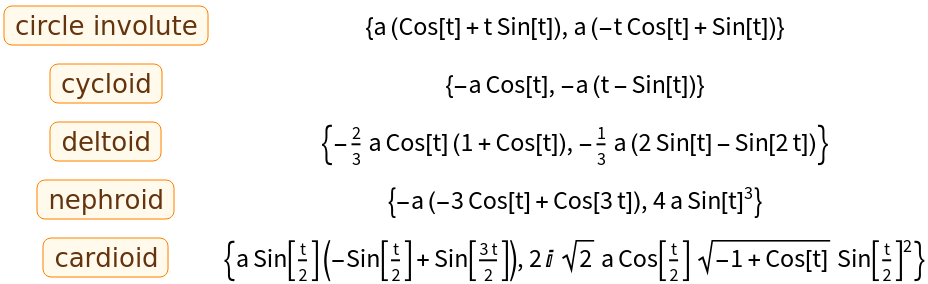

Natural equations for some curves can be solved in terms of elementary functions. Get the equation for a logarithmic spiral:

In[3]:=
spiral = Entity["PlaneCurve", "LogarithmicSpiral"][ "ParametricEquations"][a, b][t]
Out[3]=

Get the natural equations:

In[4]:=
ResourceFunction["NaturalEquations"][spiral, t] // PowerExpand
Out[4]=

Options (1) 

Assumptions (1) 

Use the option Assumptions to specify assumptions:

In[5]:=
ResourceFunction["NaturalEquations"][ Entity["PlaneCurve", "Lemniscate"]["ParametricEquations"][a][t], t, Assumptions -> a > 0 && t > 0]
Out[5]=

Properties and Relations (2) 

The Cornu spiral:

In[6]:=
spiral = Entity["PlaneCurve", "CornuSpiral"]["ParametricEquations"][a, b][t]
Out[6]=

NaturalEquations gives the same result:

In[7]:=
ResourceFunction["NaturalEquations"][spiral, t] // PowerExpand
Out[7]=

Alfred Gray’s generalization of the Cornu spiral:

In[8]:=
clothoid[n_, a_][s_] := \!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(s\)]\(\(clothoidprime[ n, a]\)[ss] \[DifferentialD]ss\)\) clothoid[a_][s_] := {a Sqrt[\[Pi]] FresnelS[s/Sqrt[\[Pi]]], a Sqrt[\[Pi]] FresnelC[s/Sqrt[\[Pi]]]} clothoidprime[n_, a_][t_] := {a Sin[t^(n + 1)/(n + 1)], a Cos[t^(n + 1)/(n + 1)]}

In this case, the resulting natural equations contain special functions:

In[9]:=
ResourceFunction["NaturalEquations"][clothoid[n, a][t], t]
Out[9]=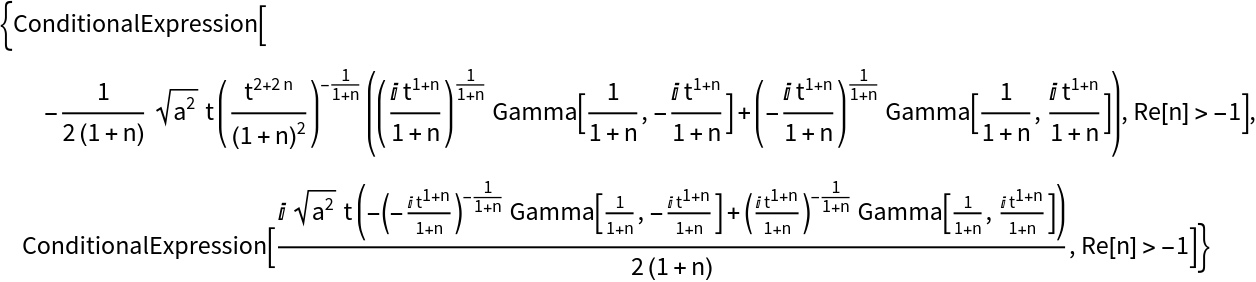

Using assumptions can simplify the resulting expressions:

In[10]:=
FullSimplify[%, n \[Element] PositiveIntegers && a > 0]
Out[10]=

Get equations for the clothoid prime curve (the velocity of the nth clothoid):

In[11]:=
ResourceFunction["NaturalEquations"][clothoidprime[n, a][t], t]
Out[11]=

Simplifying:

In[12]:=
FullSimplify[%, n \[Element] PositiveIntegers && a > 0]
Out[12]=

Possible Issues (2) 

Some cases can give large results:

In[13]:=
ResourceFunction["NaturalEquations"][ Entity["PlaneCurve", "TschirnhausenCubic"]["ParametricEquations"][ a][t], t] // PowerExpand
Out[13]=

But they can often be simplified:

In[14]:=
FullSimplify[%, t > 0]
Out[14]=

Cassini curve:

In[15]:=
cassini[a_, b_, pm1_, pm2_][ t_] := {pm1 Sqrt[a^2 Cos[2 t] + pm2 Sqrt[b^4 - a^4 Sin[2 t]^2]] Cos[t], pm1 Sqrt[a^2 Cos[2 t] + pm2 Sqrt[b^4 - a^4 Sin[2 t]^2]] Sin[t]}

Some cases need some time to evaluate:

In[16]:=
ResourceFunction["NaturalEquations"][cassini[1, 1, 1, 1][t], t] // PowerExpand // Timing
Out[16]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 12 June 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information