Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a numerical approximation for a trigonometric Fourier series expansion of a function
ResourceFunction["NFourierTrigSeries"][expr,t,n] gives a numerical approximation to the nth-order Fourier trigonometric series expansion of expr in t. |
Numerical approximation for a trigonometric Fourier series:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 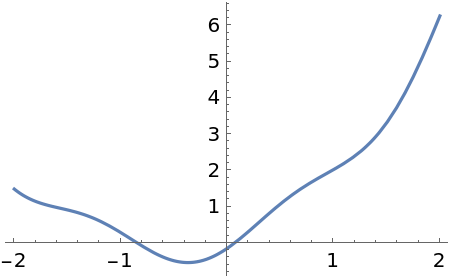 |
Compare with a plot of the original function:
| In[3]:= |
| Out[3]= | 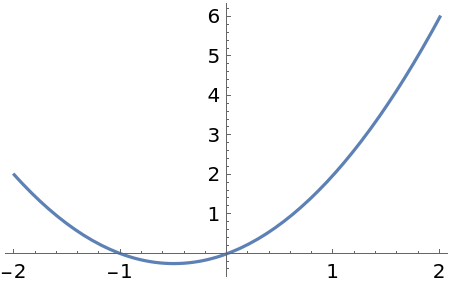 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License