Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NFourierTransform

Source Notebook

Find a numerical approximation for a Fourier transform

Contributed by: Wolfram Research

ResourceFunction["NFourierTransform"][expr,t,ω]

gives a numerical approximation to the Fourier transform of expr evaluated at the numerical value ω, where expr is a function of t.

Details and Options

The numerical approximation to the Fourier transform of expr is by default defined to be .
Different choices for the definition of the Fourier transform can be specified using the option FourierParameters.
With the setting FourierParameters→{a,b}, the Fourier transform computed by ResourceFunction["NFourierTransform"] is .
The parameter b in the setting FourierParameters→{a,b} must be numeric.
In addition to the option FourierParameters, ResourceFunction["NFourierTransform"] can also accept the options available to NIntegrate. These options are passed directly to NIntegrate.

Examples

Basic Examples (2) 

Numerical Fourier transform for a box function:

In[1]:=
f[t_] := UnitStep[1 - t] UnitStep[t + 1]
In[2]:=
Plot[ResourceFunction["NFourierTransform"][f[t], t, \[Omega]], {\[Omega], -20, 20}, PlotRange -> All]
Out[2]=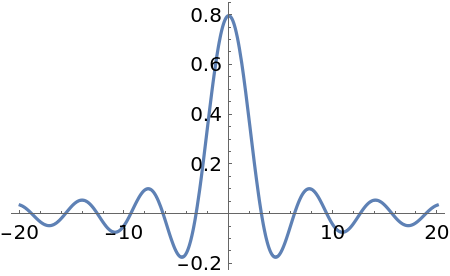

Compare with the answer from symbolic evaluation:

In[3]:=
ResourceFunction["NFourierTransform"][f[t], t, 0.7]
Out[3]=
In[4]:=
FourierTransform[f[t], t, \[Omega]]
Out[4]=
In[5]:=
% /. {\[Omega] -> 0.7}
Out[5]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 03 April 2019

Related Resources

License Information