Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NEigenvalueSumGradient

Source Notebook

Numerically evaluate the gradient of a function summed over the eigenvalues of a matrix, with respect to matrix parameters

Contributed by: Carl Woll

ResourceFunction["NEigenvalueSumGradient"][f, m][x, y, …]

finds the gradient of the function f summed over the eigenvalues of the matrix m[x,y,…].

Details and Options

The function f should be a unary differentiable or symbolic function.
The function m should be a differentiable function of the variables x, y, … that returns a square matrix.
The matrix should be numeric when the variables are numeric.
ResourceFunction["NEigenvalueSumGradient"] works with both symmetric and non-symmetric matrices.
ResourceFunction["NEigenvalueSumGradient"] works with large numerical matrices that are a function of variables x, y, ….

Examples

Basic Examples (3) 

Define a symmetric matrix function:

In[1]:=
SeedRandom[49]; mat[x_, y_] = (# + Transpose[#]) &[ RandomInteger[10, {3, 3}] + RandomInteger[ 10, {3, 3}] (RandomChoice[{x, y}, {3, 3}]^ RandomInteger[5, {3, 3}])];

Find the gradient of the eigenvalue function #Log[#]& summed over the eigenvalues at x=1, y=1:

In[2]:=
ResourceFunction["NEigenvalueSumGradient"][# Log[#] &, mat][1, 1]
Out[2]=

Check:

In[3]:=
eigs = Eigenvalues[mat[x, y]]; D[Total[eigs Log[eigs]], {{x, y}}] /. {x -> 1., y -> 1.}
Out[4]=

Scope (3) 

A non-symmetric matrix:

In[5]:=
SeedRandom[42]; mat[x_, y_] = RandomInteger[10, {3, 3, 2}] . {1, I} + RandomInteger[ 10, {3, 3}] (RandomChoice[{x, y}, {3, 3}]^ RandomInteger[5, {3, 3}]); mat[x, y] // MatrixForm
Out[7]=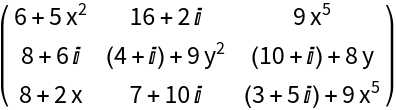

Find the gradient of the function Sin[#]Log[#]& summed over the eigenvalues at x=1, y=1:

In[8]:=
ResourceFunction["NEigenvalueSumGradient"][Sin[#] Log[#] &, mat][1, 1]
Out[8]=

Check:

In[9]:=
eigs = Eigenvalues[mat[x, y]]; D[Total[Sin[eigs] Log[eigs]], {{x, y}}] /. {x -> 1., y -> 1.}
Out[10]=

A somewhat large matrix with two parameters:

In[11]:=
SeedRandom[1]; n = 10; mat[x_, y_] = RandomReal[1, {n, n}] + RandomReal[ 10, {n, n}] (RandomChoice[{x, y}, {n, n}]^ RandomInteger[5, {n, n}]);

Finding the eigenvalues of even a moderately large matrix with symbolic parameters is slow:

In[12]:=
eigs = Eigenvalues[mat[x, y]]; // AbsoluteTiming
Out[12]=

Using NEigenvalueSumGradient is quick:

In[13]:=
ResourceFunction["NEigenvalueSumGradient"][# Log[#] &, mat][1, 1] // AbsoluteTiming
Out[14]=

Check:

In[15]:=
D[Total[eigs Log[eigs]], {{x, y}}] /. {x -> 1., y -> 1.} // AbsoluteTiming
Out[15]=

Very large matrix:

In[16]:=
SeedRandom[1]; n = 1000; mat[x_, y_] = RandomReal[1, {n, n}] + RandomReal[ 1, {n, n}] (RandomChoice[{x, y}, {n, n}]^ RandomInteger[5, {n, n}]);

Using NEigenvalueSumGradient is reasonably quick:

In[17]:=
ResourceFunction["NEigenvalueSumGradient"][Log, mat][1, 1] // AbsoluteTiming
Out[17]=

Publisher

Carl Woll

Version History

  • 1.0.0 – 24 October 2019

License Information