Function Repository Resource:

NDerivative

Source Notebook

Find a numerical approximation to a function derivative near the specified point

Contributed by: Wolfram Research

ResourceFunction["NDerivative"][expr,x,x₀]

gives a numerical approximation to the derivative of expr with respect to x at the point x₀.

ResourceFunction["NDerivative"][expr,{x,n},x₀]

gives a numerical approximation to the n^th derivative of expr.

Details and Options

The expression expr must be numeric when its argument x is numeric.

ResourceFunction["NDerivative"][expr,x,x₀] is equivalent to ResourceFunction["NDerivative"][expr,{x,1},x₀].

ResourceFunction["NDerivative"] is unable to recognize small numbers that should in fact be zero. Chop may be needed to eliminate these spurious residuals.

The following options can be given:

Method

"EulerSum"

method to use

"Scale"

size at which variations are expected

"Terms"

number of terms to be used

WorkingPrecision

MachinePrecision

precision to use in internal computations

Possible settings for Method include:

"EulerSum"

use Richardson’s extrapolation to the limit

NIntegrate

use Cauchy’s integral formula

With Method→"EulerSum", ResourceFunction["NDerivative"] needs to evaluate expr at x₀.

If expr is not analytic in the neighborhood of x₀, then the default method "EulerSum" must be used.

The option "Scale"→s is used to capture the scale of variation when using Method→"EulerSum".

When the value of the derivative depends on the direction, the default is to the right. Other directions can be chosen with the option "Scale"→s, where the direction is s.

The option "Terms"→n gives the number of terms to use for extrapolation when using Method→"EulerSum".

With Method→NIntegrate, the expression expr must be analytic in a neighborhood of the point x₀.

The option "Scale"→r specifies the radius of the contour of integration to use with Method→NIntegrate.

Examples

Basic Examples (2)

Take the numerical derivative of an exponential:

In[1]:=

Out[1]=

Take the numerical derivative of a trig power:

In[2]:=

$ResourceFunction["NDerivative"][Cos[x]^3, {x, 2}, 0]$

Out[2]=

Scope (1)

The expression and evaluation point may be complex valued:

In[3]:=

$ResourceFunction["NDerivative"][Sin[x], x, \[Pi] I]$

Out[3]=

In[4]:=

Out[4]=

Generalizations & Extensions (1)

NDerivative threads over its first argument:

In[5]:=

Out[5]=

Options (16)

Method (2)

Use the default Method→"EulerSum" when expr is not analytic in the neighborhood of x₀:

In[6]:=

Out[6]=

Check:

In[7]:=

Out[7]=

An incorrect answer is obtained with Method→NIntegrate:

In[8]:=

Out[8]=

Here is a derivative where the default method works poorly:

In[9]:=

$ResourceFunction["NDerivative"][Exp[x^2], {x, 3}, 1]$

Out[9]=

The correct answer is:

In[10]:=

$D[Exp[x^2], {x, 3}] /. x -> 1.$

Out[10]=

In this case the expression is analytic, so Method→NIntegrate will work well:

In[11]:=

$ResourceFunction["NDerivative"][Exp[x^2], {x, 3}, 1, Method -> NIntegrate]$

Out[11]=

Scale (3)

Use Scale→s to capture the region of variation:

In[12]:=

Out[12]=

The scale of variation is around .01:

In[13]:=

Out[13]=

A value of Scale→s that is too large can be compensated by increasing the number of terms:

In[14]:=

Out[14]=

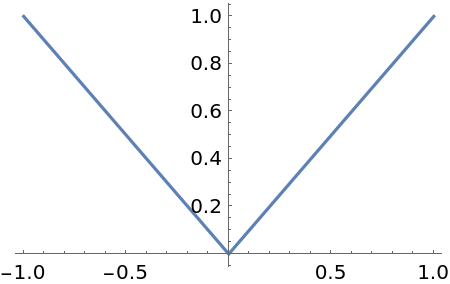
Use Scale to specify directional derivatives. The left and right derivatives of the nonanalytic function |x|:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Check:

In[17]:=

Out[17]=

Complex directions may also be specified:

In[18]:=

Out[18]=

Check:

In[19]:=

Out[19]=

Use the option Scale to avoid regions of nonanalyticity when the method used is NIntegrate:

In[20]:=

Out[20]=

Shrinking the radius avoids the essential singularity at x⩵1:

In[21]:=

Out[21]=

Check:

In[22]:=

Out[22]=

Terms (5)

Increasing the number of terms may improve accuracy. Here is a somewhat inaccurate approximation:

In[23]:=

$ResourceFunction["NDerivative"][Sin[x^2], {x, 3}, 1]$

Out[23]=

Check:

In[24]:=

$D[Sin[x^2], {x, 3}] /. x -> 1`30$

Out[24]=

Increasing the number of terms produces a more accurate answer:

In[25]:=

$ResourceFunction["NDerivative"][Sin[x^2], {x, 3}, 1, "Terms" -> 10] // FullForm$

Out[25]=

Increasing the number of terms further can produce nonsense due to numerical instability:

In[26]:=

$ResourceFunction["NDerivative"][Sin[x^2], {x, 3}, 1, "Terms" -> 20]$

Out[26]=

Combining an increase in the number of terms with a higher working precision often will reduce the error:

In[27]:=

$ResourceFunction["NDerivative"][Sin[x^2], {x, 3}, 1, "Terms" -> 20, WorkingPrecision -> 40]$

Out[27]=

WorkingPrecision (6)

High-order derivatives with Method→"EulerSum" experience significant subtractive cancellation:

In[28]:=

Out[28]=

Using a higher working precision and additional terms produces an accurate answer:

In[29]:=

Out[29]=

For this problem, Method→NIntegrate with default options produces a correct answer:

In[30]:=

Out[30]=

Higher-order derivatives will again experience numerical instability:

In[31]:=

Out[31]=

Increasing WorkingPrecision will improve the accuracy:

In[32]:=

Out[32]=

An alternative is to increase the radius of the contour of integration:

In[33]:=

Out[33]=

Applications (4)

NDerivative is useful for differentiating functions that are only defined numerically. Here is such a function:

In[34]:=

$f[a_?NumericQ, b_?NumericQ] := f[a, b] = Module[{t}, y /. NDSolve[{y'[t] == a - b y[t]^3, y[0] == 1}, y, {t, 0, 1}][[ 1]]]$

Here is the derivative of f[a,b][t] with respect to b evaluated at {a,b,t}={1,2,1}:

In[35]:=

Out[35]=

NDerivative can be used as an aid in developing and testing a more robust function for finding the derivative:

In[36]:=

$fb[a_?NumericQ, b_?NumericQ] := fb[a, b] = Module[{t}, yb /. NDSolve[{y'[t] == a - b y[t]^3, yb'[t] == -y[t]^3 - 3 b y[t]^2 yb[t], y[0] == 1, yb[0] == 0}, {y, yb}, {t, 0, 1}][[1]]]$