Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NDSolveAround

Source Notebook

Propagate Gaussian uncertainty through NDSolve

Contributed by: Collin Marino

ResourceFunction["NDSolveAround"][eqns,{u},{x,xmin,xmax}]

numerically solves ordinary differential equations eqns containing Around quantities for the function u with the independent variable x in the range xmin to xmax.

ResourceFunction["NDSolveAround"][eqns,{u},{x,xmin,xmax},{y,ymin,ymax}]

solves the partial differential equations eqns over a rectangular region.

ResourceFunction["NDSolveAround"][eqns,{u},{x,y}∈Ω]

solves the partial differential equations eqns over the region Ω.

ResourceFunction["NDSolveAround"][eqns,{u},{t,tmin,tmax},{x,y}∈Ω]

solves the time-dependent partial differential equations eqns over the region Ω.

ResourceFunction["NDSolveAround"][eqns,{u1,u2,...},...]

solves eqns for the functions ui.

Details and Options

ResourceFunction["NDSolveAround"] takes all the options of NDSolve.
ResourceFunction["NDSolveAround"] uses the numerical differentiation function ND and numerical summation function EulerSum from the NumericalCalculus standard package.
The following additional options can also be specified:
"AroundReplaceOrder"1series expansion to order by which the uncertainty is propagated
"NDOptions"{Method -> EulerSum}options to pass to internal calls of ND
"AroundReplaceOrder" can be an integer from 1 to 4.
EulerSum is the only currently supported ND method, however other options can be passed to ND.
It is assumed that all Around values are independant of one another (all covariances are assumed to be zero).

Examples

Basic Examples (3) 

Solve a first-order ordinary differential equation with uncertainty:

In[1]:=
s = ResourceFunction[ "NDSolveAround"][{y'[x] == y[x] Cos[Around[1, 0.1] (x + y[x])], y[0] == 1}, {y}, {x, 0, 30}];

Plot the solution with error bars:

In[2]:=
ListLinePlot[Table[{x, s[[1]][x]}, {x, 0, 30, 0.25}], PlotRange -> All]
Out[2]=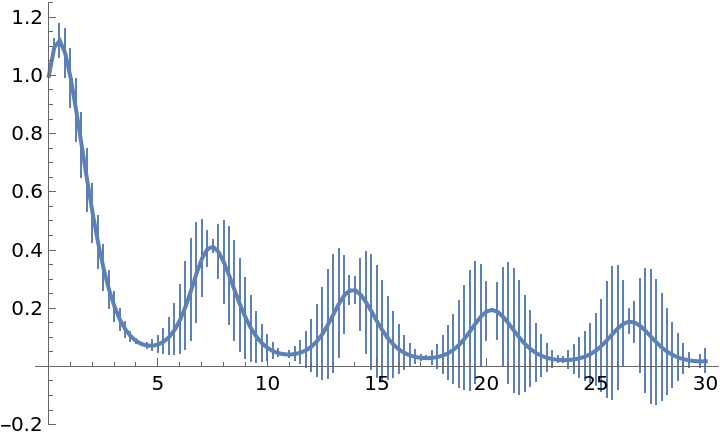

Plot the function and its derivative with 2D error bars:

In[3]:=
ListLinePlot[Table[Evaluate[{s[[1]][x], Around[\!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Value\>"])\)\), \!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Uncertainty\>"])\)\)]}], {x, 0.01, 7.5, 0.1}], InterpolationOrder -> Automatic]
Out[3]=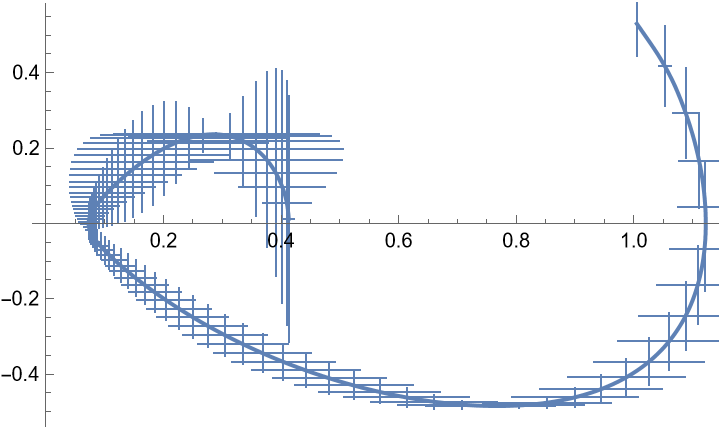

Compute the derivatives of the "Value" and "Uncertainty" of the Around quantities independently and re-bundle them inside of Around:

In[4]:=
{s[[1]][10.5], Around[\!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Value\>"])\)\), \!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Uncertainty\>"])\)\)] /. x -> 12.5}
Out[4]=

System of ordinary differential equations with uncertainty in the parameters:

In[5]:=
s = ResourceFunction["NDSolveAround"][{ x'[t] == -y[t] - Around[1, 0.05]*x[t]^2, y'[t] == Around[2, 0.04]* x[t] - y[t]^3, x[0] == 1, y[0] == 1 }, {x, y}, {t, 20}];
In[6]:=
ListLinePlot[Table[Evaluate[{s[[1]][x], Around[\!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Value\>"])\)\), \!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\((\(\(s[\([\)\(1\)\(]\)]\)[ x]\)["\<Uncertainty\>"])\)\)]}], {x, 0.01, 10, 0.1}], InterpolationOrder -> Automatic, PlotMarkers -> \[FilledSmallCircle]]
Out[6]=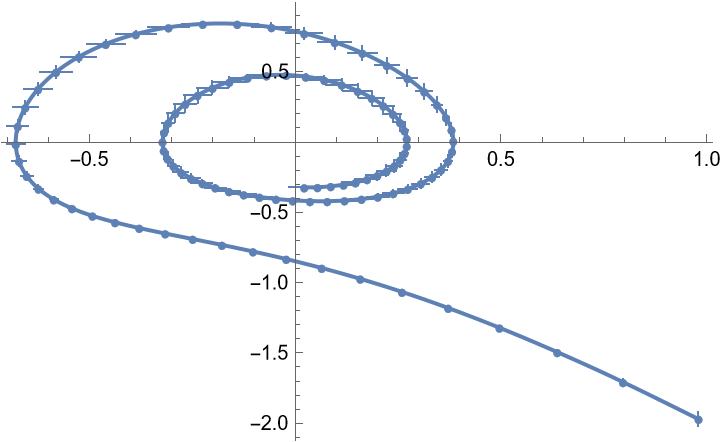

Solve the heat equation in one dimension with uncertainty in the thermal diffusivity:

In[7]:=
sol = ResourceFunction["NDSolveAround"][{ D[u[t, x], t] == Around[1, 1] D[u[t, x], x, x], u[0, x] == 0, u[t, 0] == Sin[t], u[t, 5] == 0 }, {u}, {t, 0, 10}, {x, 0, 5}];
In[8]:=
points = Flatten[Table[{t, x, sol[[1]][t, x]}, {t, 0, 10, 0.1}, {x, 0, 5, 0.1}], 1]; lowerbound = points /. a_Around :> a["Interval"][[1, 1]]; upperbound = points /. a_Around :> a["Interval"][[1, 2]]; ListPlot3D[{points, lowerbound, upperbound}, PlotRange -> All, PlotStyle -> {Automatic, Directive[ColorData[97, 4]], Directive[ColorData[97, 1]]}]
Out[11]=

Options (2) 

AroundReplaceOrder (1) 

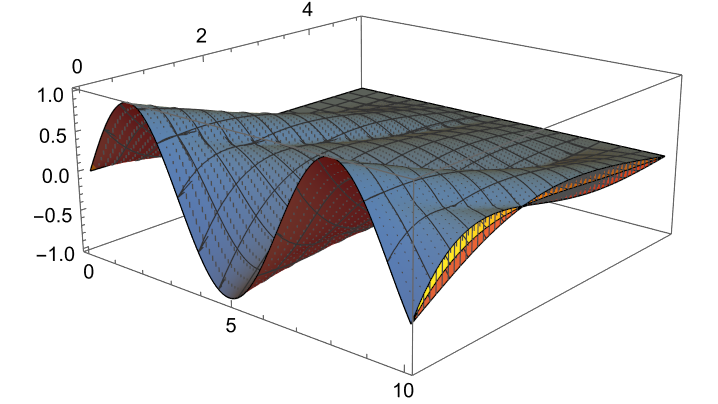Use higher order series expansions to propagate the gaussian error:

In[12]:=
sols = Table[ResourceFunction["NDSolveAround"][{\!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == Around[-9.8, 1]*\[Theta][t], \[Theta][0] == \[Pi]/ 4, \[Theta]'[0] == 0 }, {\[Theta]}, {t, 0, 10}, "AroundReplaceOrder" -> n, "NDOptions" -> {Terms -> 6, Scale -> 2}], {n, 1, 4}]; GraphicsGrid@ Partition[ Table[ListLinePlot[Table[{t, sols[[n]][[1]][t]}, {t, 0, 10, 0.1}], PlotLabel -> "\"AroundReplaceOrder\" -> " <> ToString[n], PlotRange -> All], {n, 1, Length[sols]}], 2]
Out[13]=

NDOptions (1) 

Pass options to ND from the NumericalCalculus` package:

In[14]:=
sol = ResourceFunction[ "NDSolveAround"][{y'[x] == y[x] Cos[Around[1, 0.05] (x + y[x])], y[0] == 1}, {y}, {x, 0, 30}, "AroundReplaceOrder" -> 4, "NDOptions" -> {Scale -> 2, Terms -> 6}]; ListLinePlot[Table[{x, sol[[1]][x]}, {x, 0, 30, 0.25}], PlotRange -> All]
Out[15]=

Properties and Relations (2) 

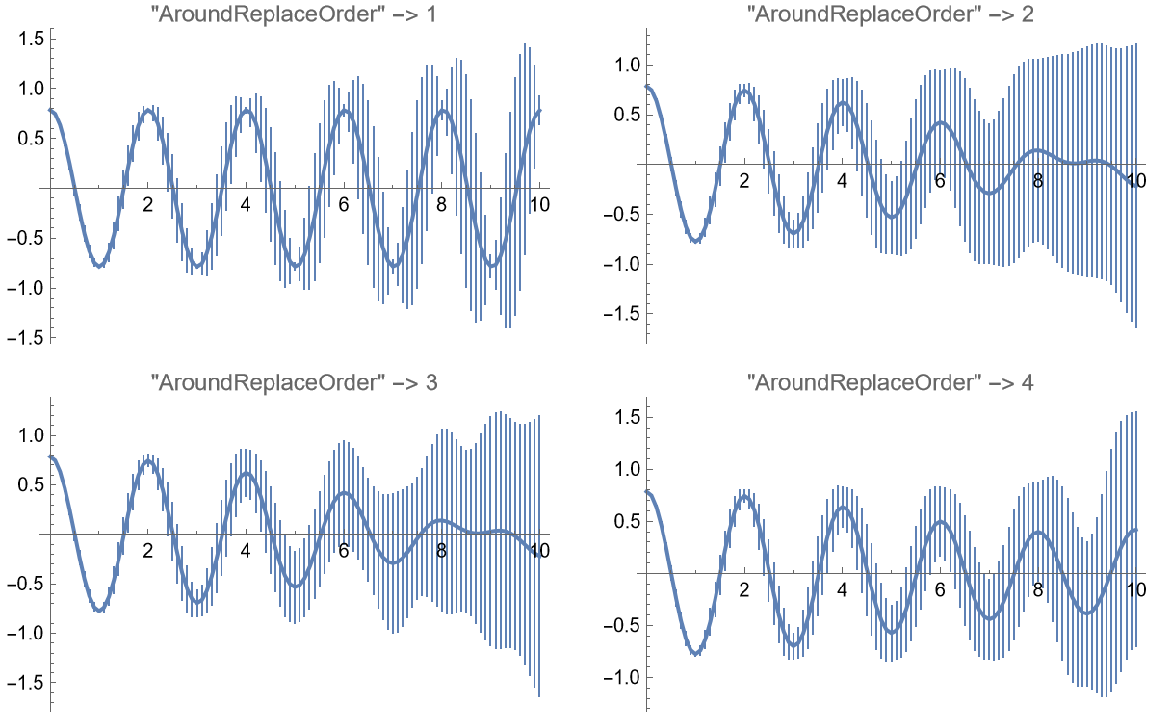Compare the results to an analytical solution using AroundReplace:

In[16]:=
L = Around[1, 0.1]; sol = L = Quantity[Around[1, 0.1], "Meters"]; g = Quantity[1, "StandardAccelerationOfGravity"]; sol = ResourceFunction["NDSolveAround"][Evaluate@{ \!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == Quantity[1, "Seconds"]^2 (-g)/L \[Theta][t], \[Theta][0] == \[Pi]/4, \[Theta]'[0] == 0 }, {\[Theta]}, {t, 0, 10}, "AroundReplaceOrder" -> 4, "NDOptions" -> {Scale -> 2, Terms -> 6}]; ListLinePlot[{ Table[{t, AroundReplace[ 1/4 \[Pi] Cos[Quantity[1, "Seconds"] (Sqrt[g] t)/Sqrt[l]], {l -> L}, 4]}, {t, 0, 10, 0.1}], Table[{t, sol[[1]][t]}, {t, 0, 10, 10/100}] }, PlotStyle -> {Automatic}, PlotLegends -> {"AroundReplace", "NDSolveAround"}]
Out[20]=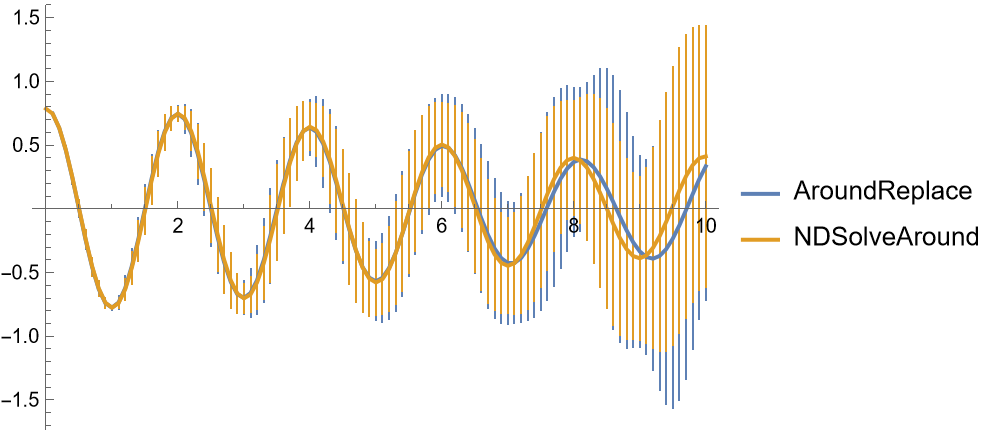

Perform a Monte Carlo Simulation and compare the results to the values predicted using NDSolveAround:

In[21]:=
SolveSystem[a_?NumericQ] := NDSolveValue[Evaluate@{\!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == a \[Theta][t], \[Theta][0] == \[Pi]/4, \[Theta]'[0] == 0}, {\[Theta]}, {t, 0, 10}]; Solutions = SolveSystem /@ RandomVariate[NormalDistribution[-9.8, 1], 1000]; MCPoints = Table[{t, Around[Mean[#], StandardDeviation[#]] &@(#[t] & /@ Solutions[[1 ;; -1, 1]])}, {t, 0, 10, 0.1}]; sol = ResourceFunction["NDSolveAround"][Evaluate@{\!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == Around[-9.8, 1]* \[Theta][t], \[Theta][0] == \[Pi]/ 4, \[Theta]'[0] == 0}, {\[Theta]}, {t, 0, 10}, "AroundReplaceOrder" -> 4, "NDOptions" -> {Scale -> 2, Terms -> 6}]; Points = Table[{t, sol[[1]][t]}, {t, 0, 10, 0.1}]; ListLinePlot[{Points, MCPoints}, PlotLegends -> {"NDSolveAround", "Monte Carlo Simulation"}]
Out[26]=

Possible Issues (2) 

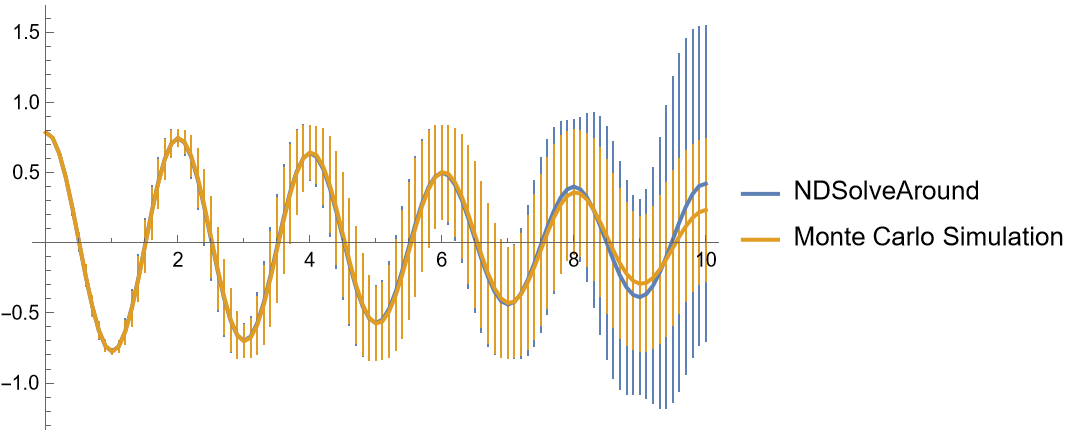In contrast to NDSolve or NDSolveValue, NDSolveAround requires the function specifications to be given in a list:

In[27]:=
Incorrect = ResourceFunction[ "NDSolveAround"][{y'[x] == y[x] Cos[Around[1, 0.1] (x + y[x])], y[0] == 1}, y, {x, 0, 30}];
In[28]:=
Incorrect[[1]][10]
Out[28]=
In[29]:=
Correct = ResourceFunction[ "NDSolveAround"][{y'[x] == y[x] Cos[Around[1, 0.1] (x + y[x])], y[0] == 1}, {y}, {x, 0, 30}];
In[30]:=
Correct[[1]][10]
Out[30]=

If the ND Scale and Terms options are not sufficient there may be significant error in the predicted values:

In[31]:=
SolveSystem[a_?NumericQ] := NDSolveValue[Evaluate@{\!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == a \[Theta][t], \[Theta][0] == \[Pi]/4, \[Theta]'[0] == 0}, {\[Theta]}, {t, 0, 10}]; Solutions = SolveSystem /@ RandomVariate[NormalDistribution[-9.8, 1], 1000]; MCPoints = Table[{t, Around[Mean[#], StandardDeviation[#]] &@(#[t] & /@ Solutions[[1 ;; -1, 1]])}, {t, 0, 10, 0.1}]; sol = ResourceFunction["NDSolveAround"][Evaluate@{\!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\[Theta][t]\)\) == Around[-9.8, 1]* \[Theta][t], \[Theta][0] == \[Pi]/ 4, \[Theta]'[0] == 0}, {\[Theta]}, {t, 0, 10}, "AroundReplaceOrder" -> 4, "NDOptions" -> {Scale -> 1, Terms -> 11}]; Points = Table[{t, sol[[1]][t]}, {t, 0, 10, 0.1}]; ListLinePlot[{Points, MCPoints}, PlotLegends -> {"NDSolveAround", "Monte Carlo Simulation"}]
Out[36]=

Publisher

Collin Marino

Requirements

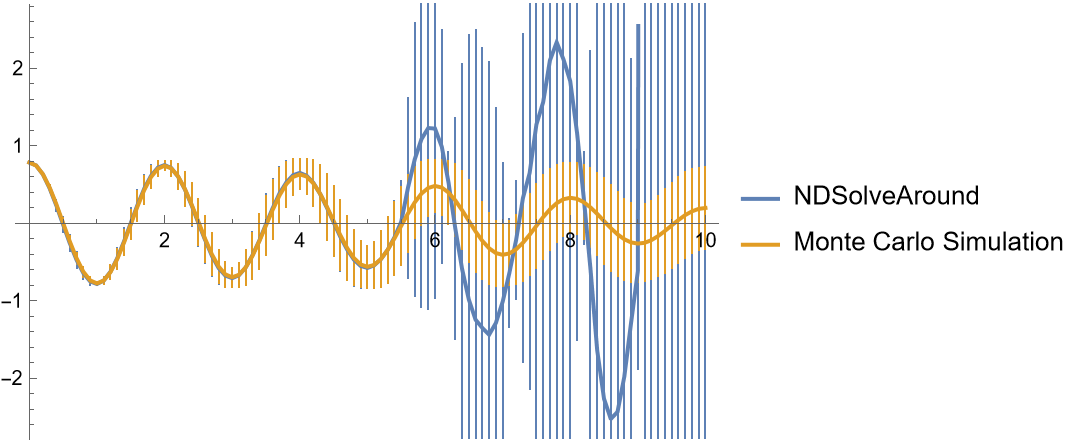Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 06 May 2024

License Information