Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Multiway state graph of a non-deterministic generalized shift
ResourceFunction["MultiwayGeneralizedShiftGraph"][{n,shift,rewrite}, init] generates a multiway state graph of a generalized shift, defined by non-deterministic shift and rewrite rules on a window of length n over a cyclic tape, starting from the initial condition init. |
| shift | {{p1,…,pn}⧴int,…} |
| rewrite | {{p1,…,pn}⧴{r1,…,rn},…} |
| {a1,…,ak} | cyclic tape of values ai with the window initially at position 1 |
| {x,{a1,…,ak}} | cyclic tape with the window intially at position x |
Create a multiway state graph of a "universal" non-deterministic generalized shift that computes all binary sequences of length 3:
| In[1]:= |
| Out[1]= |  |
Show a multiway state graph after 3 steps with improved state visualization:
| In[2]:= | ![ResourceFunction[
"MultiwayGeneralizedShiftGraph"][{2, {{__} -> 1}, {{x_, y_} :> {y, x}, {0, 0} -> {1, 0}}}, {0, 0, 0, 0, 0}, "MaxSteps" -> 3, GraphStyle -> "Basic", VertexLabels -> None, GraphLayout -> {"LayeredDigraphEmbedding", "Orientation" -> Top}, VertexShapeFunction -> (
Inset[
RulePlot[TuringMachine[{1, 1, 2}], {{1, #2[[1, 1]]}, #2[[2]]}, 0,
Frame -> False, Mesh -> All], #1, Center, 0.8] &)]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7b9e56-05c5-44ae-9a4f-6fb3fd5442fd/3b1d9fe2bf601688.png) |
| Out[2]= | 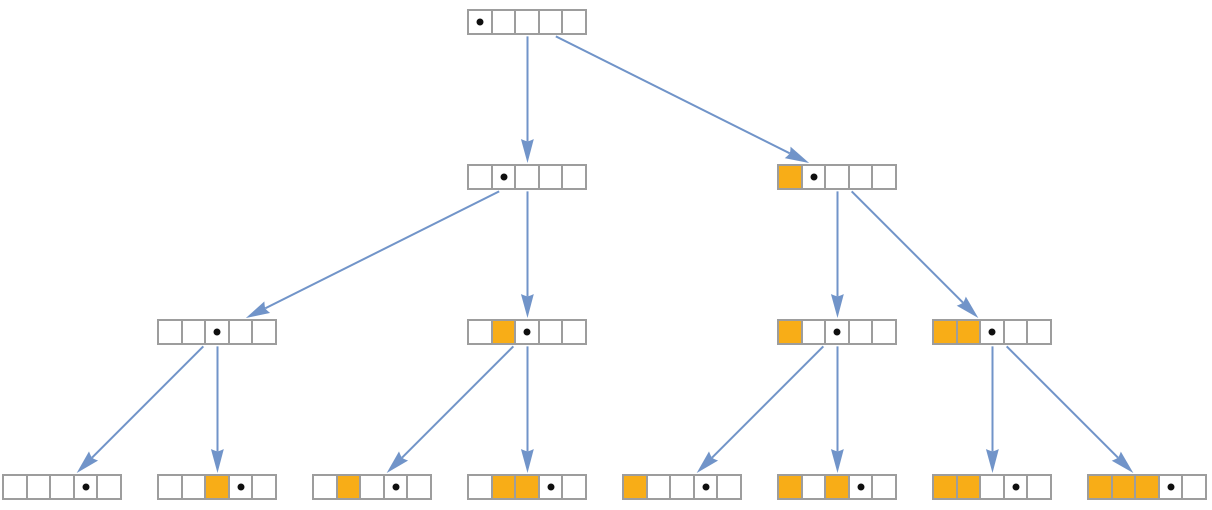 |
Create a multiway state graph:
| In[3]:= | ![gr = ResourceFunction[
"MultiwayGeneralizedShiftGraph"][{2, {{_ 1} -> 1, {0, _} -> -1}, {{x_, _} :> {x, 1}, {x_, _} :> {x, 0}, {1, 0} -> {1, 1}}}, {0, 0, 0, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7b9e56-05c5-44ae-9a4f-6fb3fd5442fd/419caa40df691dab.png) |
| Out[3]= | 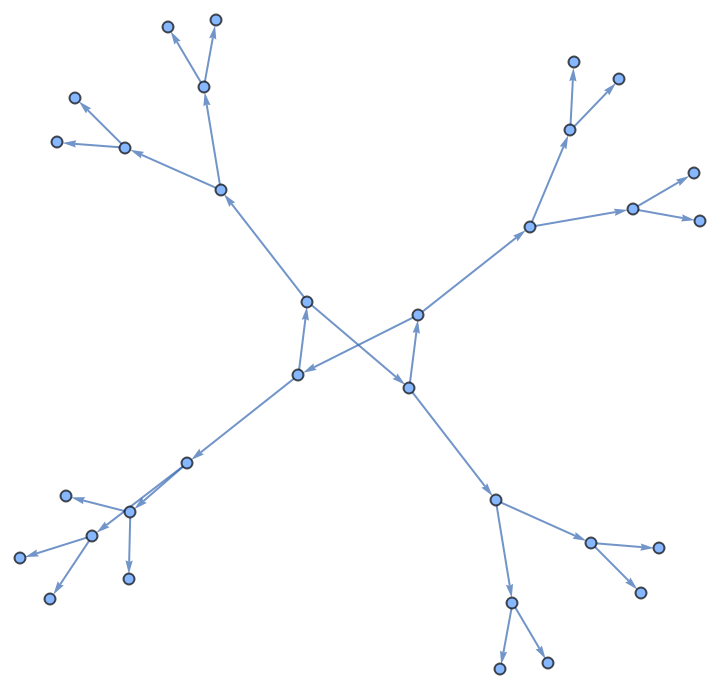 |
Identify all cyclic computations:
| In[4]:= |
| Out[4]= |
Determine the worst-case runtime to reach each state:
| In[5]:= |
| Out[5]= |
Terminate the computation at halting states:
| In[6]:= | ![haltingStateQ[{{pos_, relOrigin_}, tape_}] := Last @ tape === 1;
ResourceFunction[
"MultiwayGeneralizedShiftGraph"][{1, {{_} -> 1, {_} -> -1}, {{_} -> {1}, {_} -> {0}}}, {0, 0, 0}, "HaltingStateQ" -> haltingStateQ]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7b9e56-05c5-44ae-9a4f-6fb3fd5442fd/394cc15b3c1ebb6e.png) |
| Out[7]= | 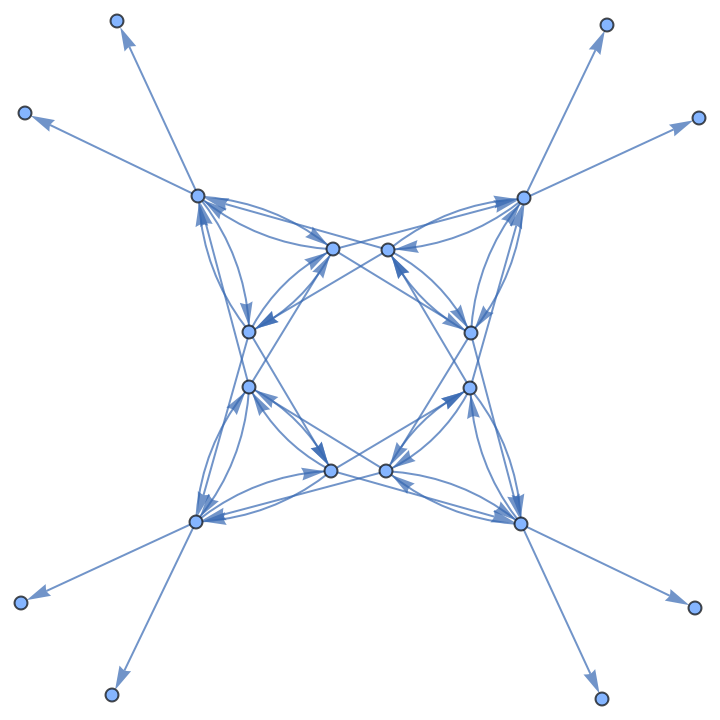 |
Terminate the computation once the maximum number of steps has been reached:
| In[8]:= |
| Out[8]= | 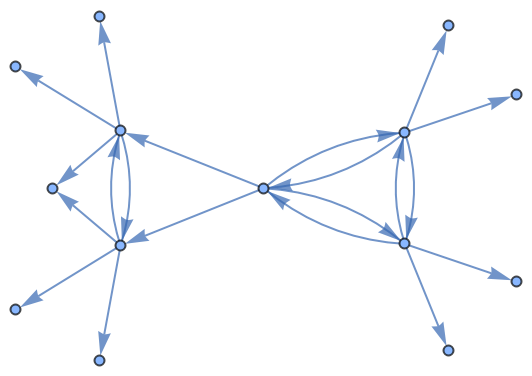 |
Randomly reduce the computational outcomes of each state, ensuring that at least one outcome remains:
| In[9]:= |
| Out[9]= | 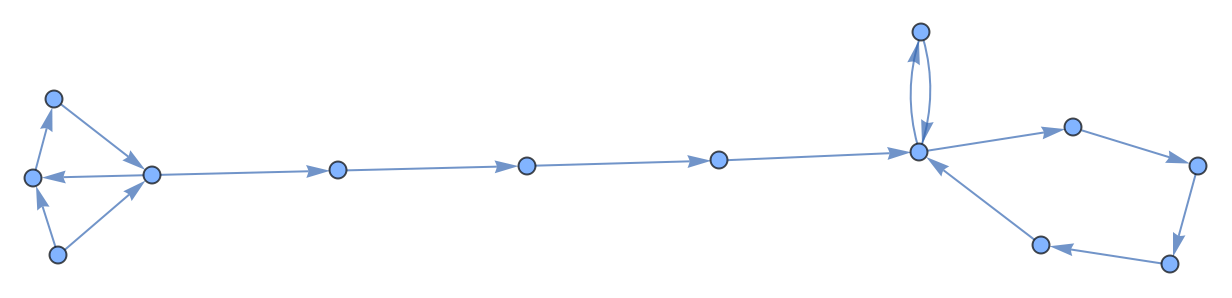 |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License