Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Explore graph traversals while deleting visited components
ResourceFunction["MultiwayDeletionsGraph"][g] returns a directed acyclic graph which maps all possible traversals of graph g while deleting vertices along the way. | |
ResourceFunction["MultiwayDeletionsGraph"][g,v1] traverses graph g starting only from initial vertex v1. | |
ResourceFunction["MultiwayDeletionsGraph"][g,{v1,v2,…,vn}] traverses graph g starting from n initial vertices vi. | |
ResourceFunction["MultiwayDeletionsGraph"][g,{v1,v2,…,vn},method] allows deleting edges by setting method equals EdgeDelete. | |
ResourceFunction["MultiwayDeletionsGraph"][g,{v1,v2,…,vn},method,max] introduces a cutoff max for cases where the state space graph g is too large to explore efficiently. |
| w1={{},v1} | an initial condition for either method, where v1∈VertexList[g] |
| wn={Sort[{v1,v2,…,vn-1}],vn} | with vi∈VertexList[g] and wn∈VertexList[ResourceFunction["MultiwayDeletionsGraph"][g,v1]] |
| wn={Sort[{e1,e2,…,en-1}],vn] | withei∈EdgeList[g]andwn∈VertexList[ResourceFunction["MultiwayDeletionsGraph"][g,v1,EdgeDelete]] |
| method=VertexDelete | First[wn]==First[wn-1]⋃{vn}&&GraphDistance[g,Last[wn-1],Last[wn]]⩵1 |
| method=EdgeDelete | First[wn]==First[wn-1]⋃{edge[vn-1,vn]}&& GraphDistance[g,Last[wn-1],Last[wn]]⩵1 |
Plot two pairs of confluent self-avoiding walks on a 2×2 GridGraph:
| In[1]:= |
| Out[1]= | 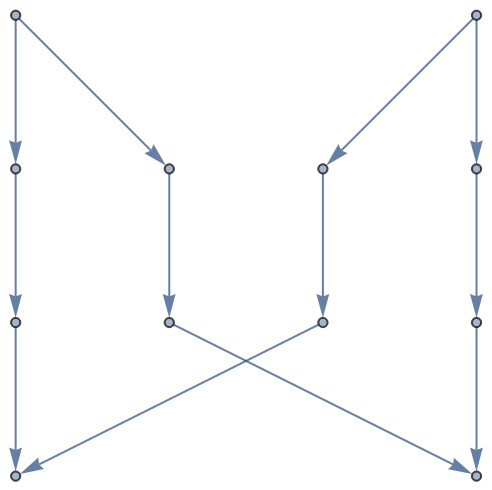 |
Add labels to see which vertices where visited when:
| In[2]:= | ![Row[{GridGraph[{2, 2}, ImageSize -> 50, VertexLabels -> (x_ :> Placed[x, Center]),
VertexSize -> Large, EdgeStyle -> Darker[Gray, .8],
VertexStyle -> Directive[White, EdgeForm[LightGray]]], Style[" \[LongRightArrow] ", Gray, Bold, 24], Grid[{WeaklyConnectedGraphComponents@
ResourceFunction["MultiwayDeletionsGraph"][GridGraph[{2, 2}],
VertexLabels -> (x_ :> Placed[Last[x], Center]),
VertexStyle -> Directive[White, EdgeForm[Gray]],
EdgeStyle -> Gray,
GraphLayout -> "LayeredDigraphEmbedding",
VertexSize -> 1/2, ImageSize -> 200, AspectRatio -> 1/2]},
Frame -> All, FrameStyle -> LightGray, Spacings -> {1, 1}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/6bd50c963d8ff32b.png) |
| Out[2]= | 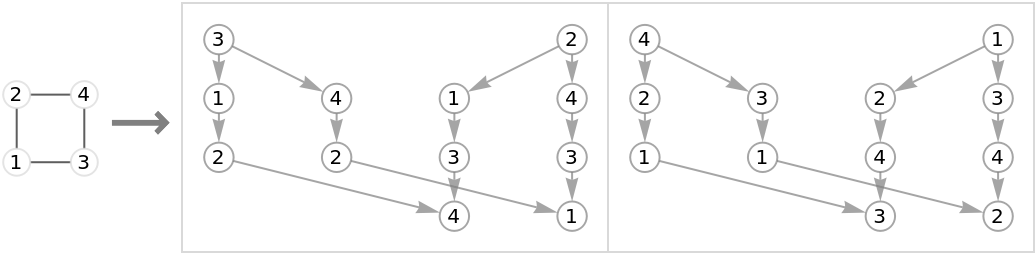 |
Graph self-avoiding walks on a 3×3 grid:
| In[3]:= |
| Out[3]= | 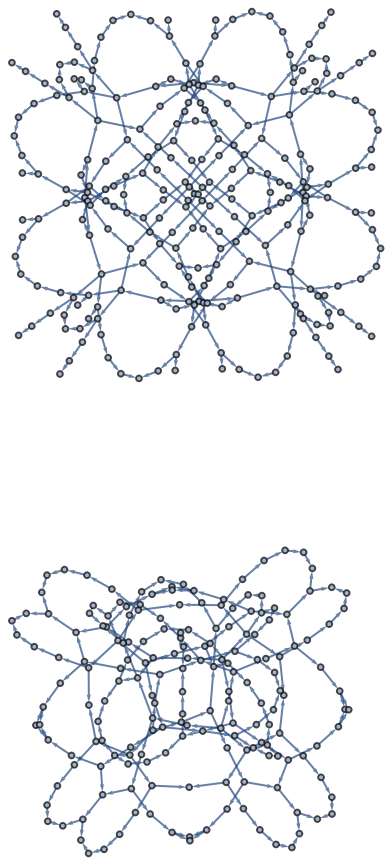 |
Only compute the subgraph starting from vertex 5:
| In[4]:= |
| Out[4]= | 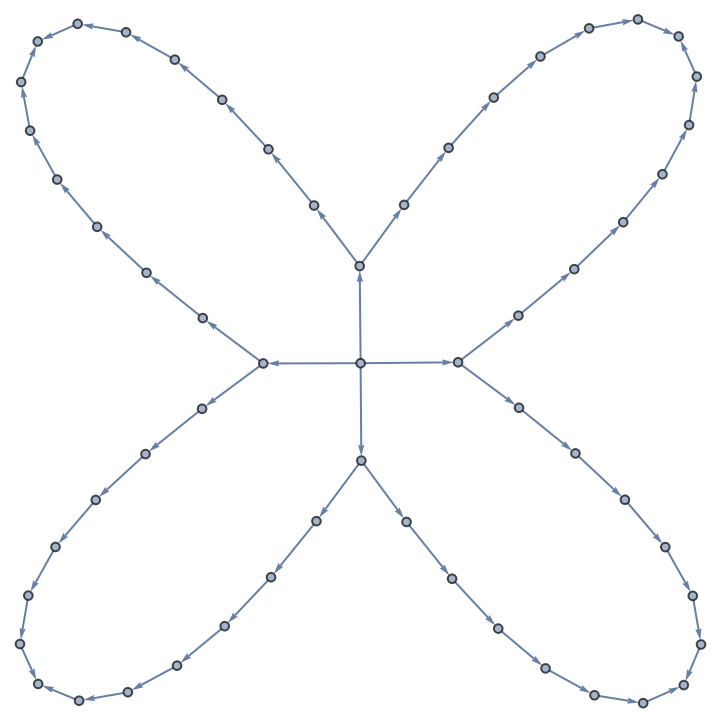 |
Decorate the graph with publication-quality icons:
| In[5]:= | ![With[{StyledDeletionsGraph = Function[{mdg, ing, ivs, vs},
Graph[mdg, VertexSize -> vs, EdgeStyle -> Gray,
VertexShapeFunction -> (Inset[HighlightGraph[Graph[ing, VertexStyle -> Directive[EdgeForm[GrayLevel[.4]], GrayLevel[.7]],
EdgeStyle -> Gray], {Style[First[#2], Hue[.55, 1, 0.9],
EdgeForm[GrayLevel[0, 0.25]]],
Style[Last[#2], Red, EdgeForm[GrayLevel[0, 0.25]]]},
VertexSize -> ivs, ImageSize -> 30], #1, Center, #3] &),
PerformanceGoal -> "Quality"]]},
StyledDeletionsGraph[
ResourceFunction["MultiwayDeletionsGraph"][GridGraph[{3, 3}], {5}],
GridGraph[{3, 3}], .75, 1.5]]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/5dc6936cd8b9d431.png) |
| Out[5]= | 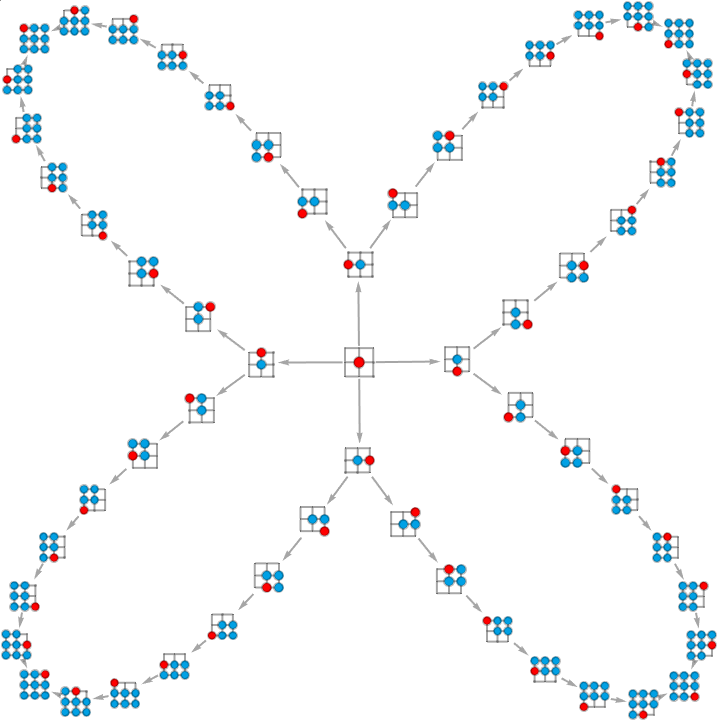 |
Allow walks from vertex 5 to intersect on vertices, but not on edges:
| In[6]:= |
| Out[6]= | 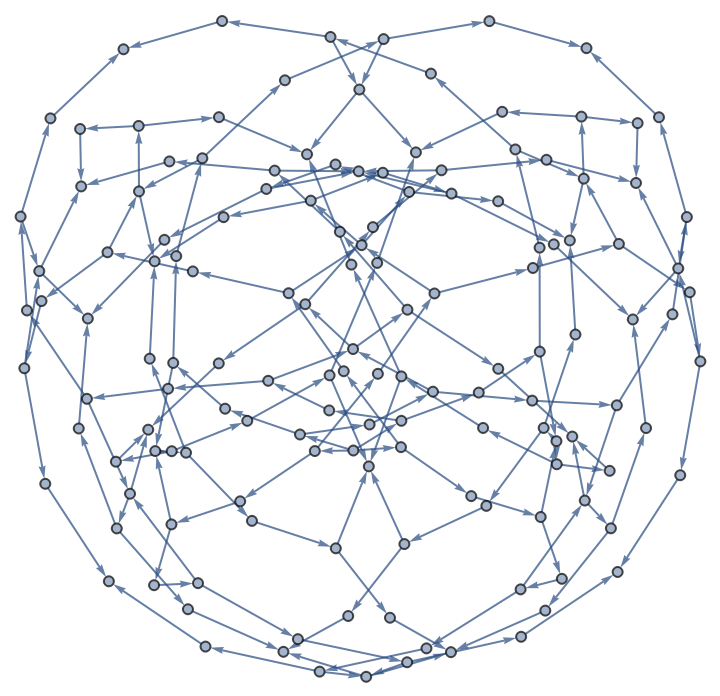 |
Again, decorate the graph with publication-quality icons:
| In[7]:= | ![With[{StyledDeletionsGraph = Function[{mdg, ing, ivs, vs},
Graph[mdg, VertexSize -> vs, EdgeStyle -> Gray,
VertexShapeFunction -> (Inset[HighlightGraph[Graph[ing, VertexStyle -> Directive[EdgeForm[GrayLevel[.4]], GrayLevel[.7]], EdgeStyle -> Directive[Darker@Gray, Thick]], {Style[
First[#2], Red,
EdgeForm[GrayLevel[0, 0.25]]],
Style[Last[#2], \!\(\*
TagBox[
StyleBox[
RowBox[{"Hue", "[",
RowBox[{"0.08`", ",", "1", ",", "1"}], "]"}],
ShowSpecialCharacters->False,
ShowStringCharacters->True,
NumberMarks->True,
"NodeID" -> 26],
FullForm]\), EdgeForm[GrayLevel[0, 0.25]]]},
VertexSize -> ivs, ImageSize -> 30], #1, Center, #3] &),
PerformanceGoal -> "Quality"]]},
StyledDeletionsGraph[
ResourceFunction["MultiwayDeletionsGraph"][GridGraph[{3, 3}], 5, EdgeDelete],
GridGraph[{3, 3}], .75, 3.5]]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/130fc891f1849600.png) |
| Out[7]= | 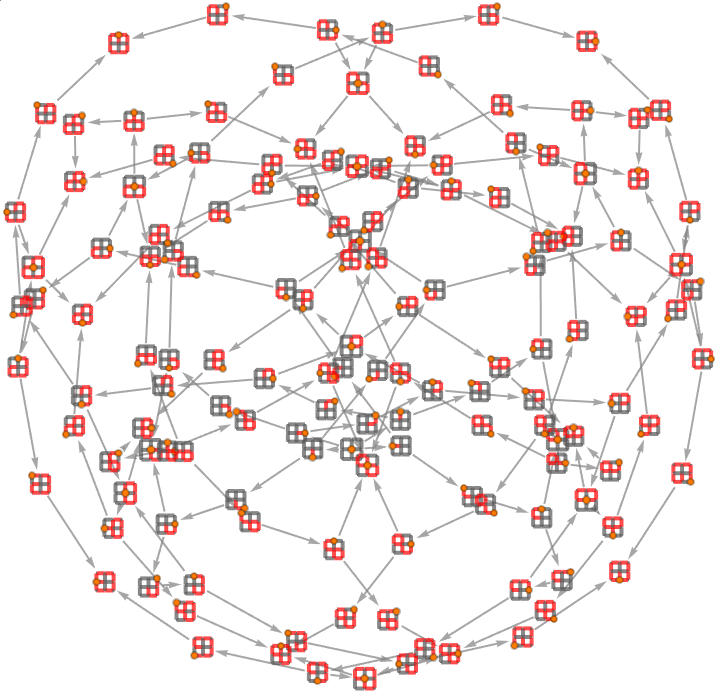 |
Test graph transformations on random inputs:
| In[8]:= | ![SeedRandom["RandTest"];
With[{ing = First[WeaklyConnectedGraphComponents[RandomGraph[{5, 7}]]]},
WeaklyConnectedGraphComponents[
ResourceFunction["MultiwayDeletionsGraph"][ing, {}, #],
GraphLayout -> "LayeredDigraphEmbedding",
AspectRatio -> 1/2] & /@ {VertexDelete, EdgeDelete}]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/6920c84847beb4f7.png) |
| Out[9]= | 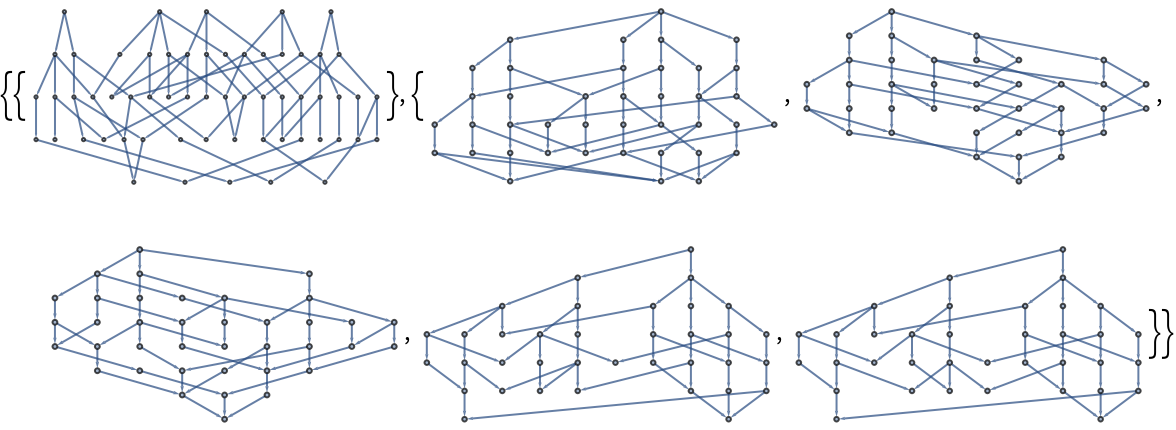 |
When inputting a directed acyclic graph, the output is always a TreeGraph:
| In[10]:= | ![With[{g0 = (SeedRandom["DAGtest"];
DirectedGraph[RandomGraph[{10, 18}], "Acyclic"])},
Grid[Partition[Labeled[Framed[Graph[#, ImageSize -> {UpTo[100], 100}],
FrameStyle -> LightGray],
Style[TreeGraphQ[#], GrayLevel[.4]]
] & /@ WeaklyConnectedGraphComponents[
ResourceFunction["MultiwayDeletionsGraph"][g0]], 5], Spacings -> {1, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/20fb4cb81c288e62.png) |
| Out[10]= | 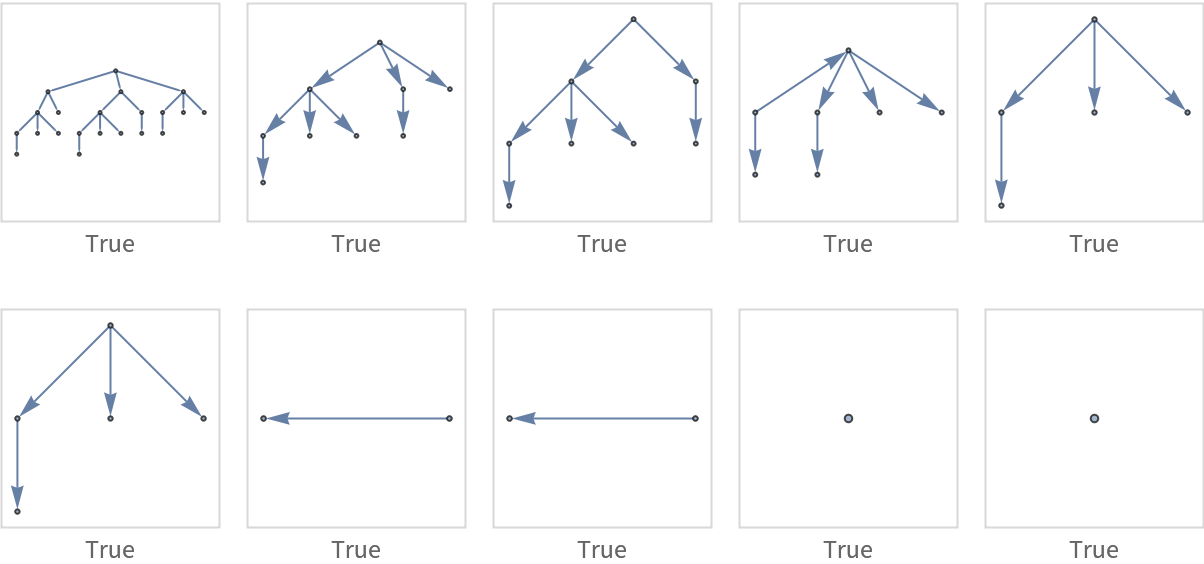 |
MultiwayDeletionsGraph automatically deduplicates edges:
| In[11]:= |
| Out[11]= |
Graph non-self-intersecting walks along the edges of a cube:
| In[12]:= |
| Out[12]= | 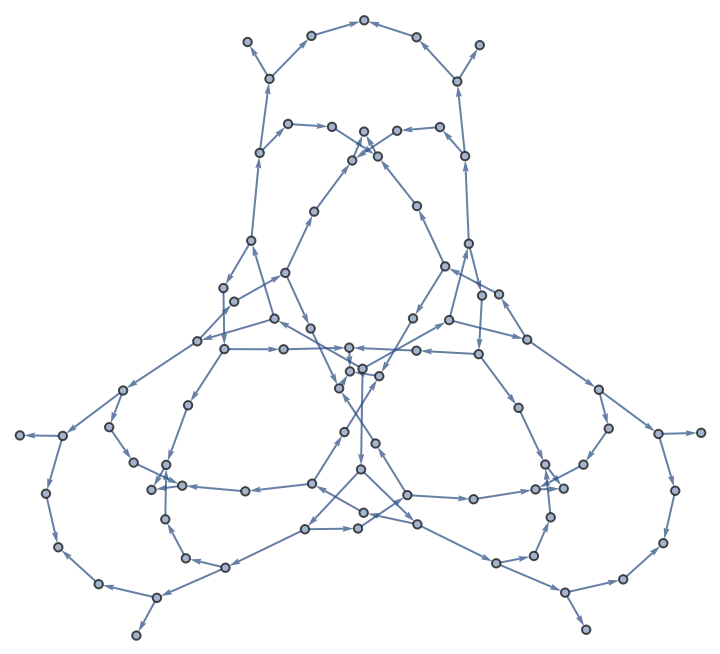 |
Find the out vertices associated with Hamiltonian cycles:
| In[13]:= | ![hcTerms = Cases[Select[VertexList[cubeWalks], Length[#[[1]]] == 7 &],
{_, Alternatives @@ VertexOutComponent[
GridGraph[{2, 2, 2}], 1, {1}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/2c32dca7cd4411fb.png) |
| Out[13]= |
Count the number of directed Hamiltonian cycles:
| In[14]:= |
| Out[14]= |
Solve Euler's bridges of Königsberg problem by computing all possible paths:
| In[15]:= | ![With[{gKonigsbergFixed = Graph[{
UndirectedEdge[n1, n2], UndirectedEdge[s1, s2],
UndirectedEdge[n1, w], UndirectedEdge[n2, w],
UndirectedEdge[s1, w], UndirectedEdge[s2, w],
UndirectedEdge[e, w], UndirectedEdge[n1, e],
UndirectedEdge[s1, e]}]},
Grid[Partition[Graph[#,
ImageSize -> {Automatic, 10 Max[Length /@ VertexList[#][[All, 1]]]}] & /@ WeaklyConnectedGraphComponents[
ResourceFunction["MultiwayDeletionsGraph"][gKonigsbergFixed, {}, EdgeDelete], GraphLayout -> "LayeredDigraphEmbedding"], 3], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b48ff511-845a-456d-b221-a3b293fc21f2/1f49d03fe66c0316.png) |
| Out[15]= | 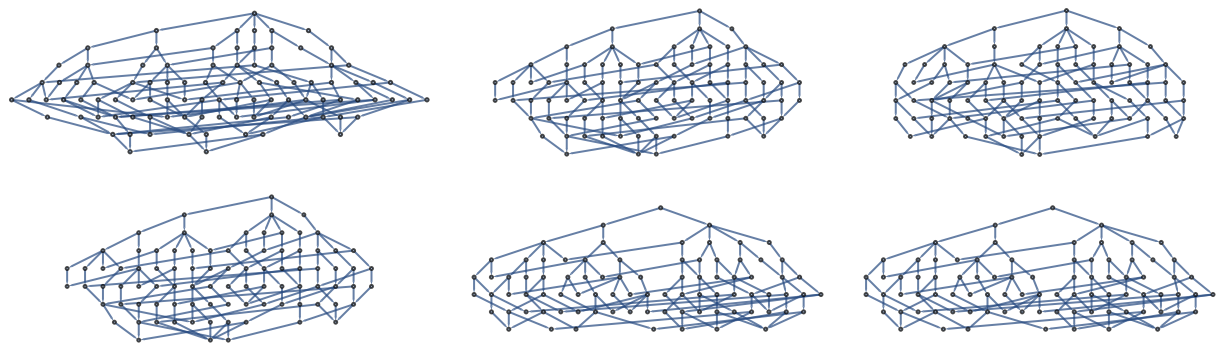 |
This work is licensed under a Creative Commons Attribution 4.0 International License