Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a multivariate Taylor polynomial of a given total degree
ResourceFunction["MultivariateTaylorPolynomial"][func,vars,n] computes the degree n multivariate Taylor polynomial of func in vars. | |
ResourceFunction["MultivariateTaylorPolynomial"][func,vars] computes the multivariate Taylor polynomial of degree 1. |
Compute a multivariate Taylor polynomial of degree 4:
| In[1]:= |
| Out[2]= |
Check the result numerically:
| In[3]:= |
| Out[4]= |
Compute constant and linear terms of an expression expanded at {x=0,y=2}:
| In[5]:= |
| Out[6]= |
Compute a multivariate Taylor polynomial around {x=1,y=-2}:
| In[7]:= |
| Out[8]= | 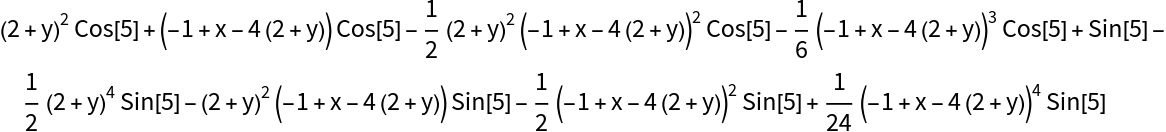 |
Check the result numerically:
| In[9]:= |
| Out[10]= |
MultivariateTaylorPolynomial can expand variables at infinity:
| In[11]:= |
| Out[12]= | 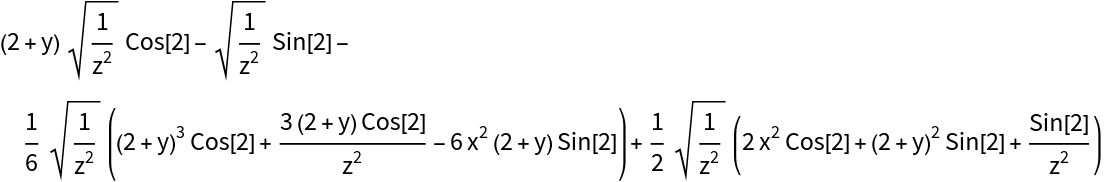 |
Providing Assumptions can simplify the computations and results:
| In[13]:= |
| Out[13]= |
Check these results numerically:
| In[14]:= |
| Out[15]= |
MultivariateTaylorPolynomial can give results that have asymptotic terms such as exponentials and implicit piecewise terms:
| In[16]:= |
| Out[17]= | 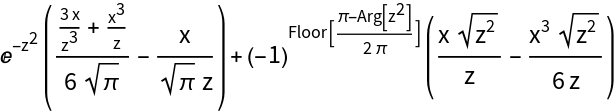 |
Provide Assumptions to obtain a simpler result:
| In[18]:= |
| Out[18]= | 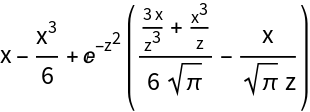 |
Check these results numerically:
| In[19]:= |
| Out[20]= |
Expand at z=-∞:
| In[21]:= |
| Out[21]= | 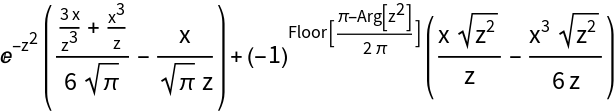 |
Check numerically:
| In[22]:= |
| Out[23]= |
Compute a multivariate expansion to seventh order:
| In[24]:= | ![ee = Sin[x + y^2]*Erf[z];
order = 7;
mm = ResourceFunction["MultivariateTaylorPolynomial"][ee, {x, y, z}, order]](https://www.wolframcloud.com/obj/resourcesystem/images/1f6/1f6b8f54-b30e-46b3-875c-4f333a581747/663a9d2c2666703d.png) |
| Out[25]= |
Use weights of {1,3,2} on the variables {x,y,z} respectively:
| In[26]:= |
| Out[26]= |
Use weights of ![]() on the variables {x,y,z} respectively:
on the variables {x,y,z} respectively:
| In[27]:= |
| Out[27]= | 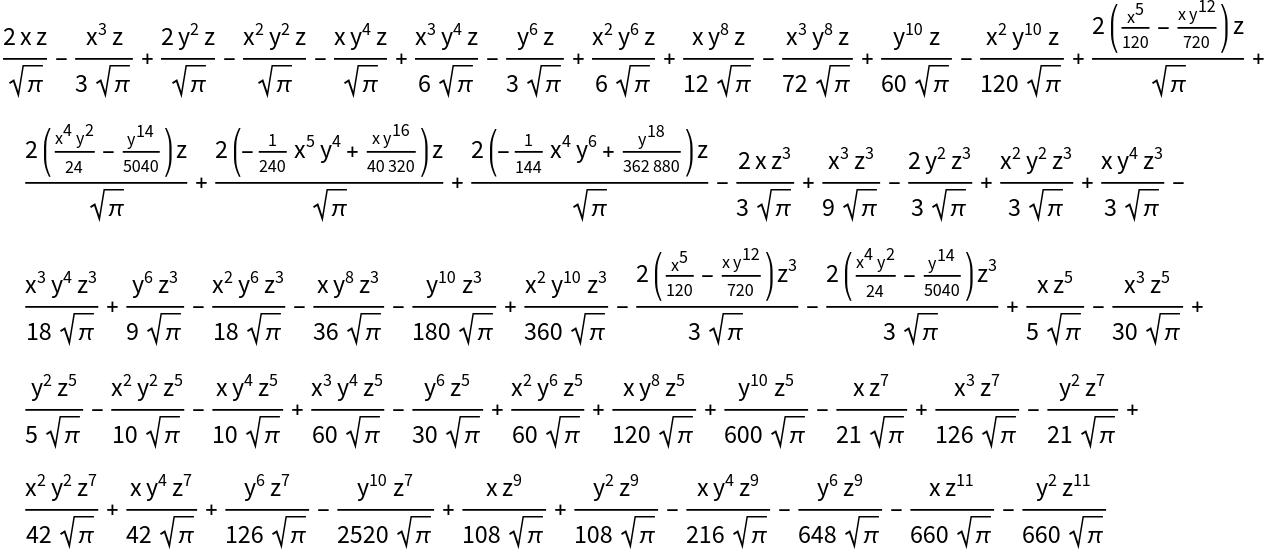 |
Compute a multivariate Taylor polynomial of total degree 4:
| In[28]:= |
| Out[29]= |
One can use Series to recover all terms by expanding in x and y separately to order 4, but this gives extra terms:
| In[30]:= |
| Out[30]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License