Function Repository Resource:

MultiReplace

Source Notebook

Perform replacements and give the positions at which they occur

Contributed by: Nikolay Murzin

ResourceFunction["MultiReplace"][expr,rule]

returns all possible subexpressions of expr after application of rule, with information about each replacement.

ResourceFunction["MultiReplace"][expr,{rule₁,rule₂,…}]

returns the result after applying a list of rules.

ResourceFunction["MultiReplace"][expr,{x₁,x₂,…}→{y₁,y₂,…}]

uses a list of patterns to replace subexpression tuples/subsets.

ResourceFunction["MultiReplace"][expr,rules,level]

specifies a level spec.

ResourceFunction["MultiReplace"][expr,rules,level,head]

uses a custom head to specify subexpression tuples/subsets.

ResourceFunction["MultiReplace"][expr,subexpr,…]

returns subexpression matches without performing substitution.

Details and Options

ResourceFunction["MultiReplace"] returns an association with keys containing a rule index and list of positions of a tuple/subset of subexpressions where the corresponding rule was applied.

If one rule is given, keys contain positions only.

Association values are the results of applying ReplaceList at corresponding positions; for a given position, multiple results of substitution are possible.

The left-hand side of a rule can be a list or a custom head to replace tuples/subsets of subexpressions, similar to SequenceReplace and SubsetReplace but for all positions.

When a list of patterns is specified as a left-hand side, replacement is applied at multiple positions, with all elements of a list being matched based on the specified "Mode".

If a rule returns a list (or a head) of expressions, they are substituted for the corresponding tuple/subset positions on the left-hand side.

ResourceFunction["MultiReplace"] takes the same options as the resource function SubexpressionPositions for subexpression selection.

ResourceFunction["MultiReplace"] takes the following options:

"Mode"

"Tuples"

how to match multiple subexpressions: "Tuples", "OrderedTuples", "Subsets" or "OrderlessSubsets"

"PatternSubstitutions"

False

whether to include pattern substitutions

"ReturnMatches"

False

return subexpression matches by ignoring the right-hand side of rules if present

Method

"Substitution"

substitution strategy to use: "Susbtitution", "Cosubstitution" or "Bisubstitution"

Heads

True

whether to match heads of expressions and their parts

Examples

Basic Examples (3)

Apply a rule at each possible position of an expression:

In[1]:=

Out[1]=

Apply multiple rules:

In[2]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][f[x, g[y]], {a_ :> h[a], b_ -> 1}]$

Out[2]=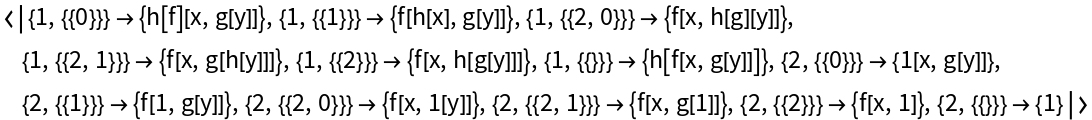

Apply a tuple replacement rule:

In[3]:=

Out[3]=

Scope (6)

Subexpressions are spliced in the order of matched elements:

In[4]:=

Out[4]=

Splicing continues after the last element:

In[5]:=

Out[5]=

A single element can be matched more than once:

In[6]:=

Out[6]=

Specify a level:

In[7]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{a, b, f[c]}, x_ :> g[x], {1}]$

Out[7]=

Specify an explicit list of positions at which to replace:

In[8]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{a, b, f[c]}, x_ :> g[x], {{1}, {-1}}]$

Out[8]=

Use a custom head for designating tuples:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Specify a matching condition:

In[12]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{1, 2, 4}, {x_, y_} /; x + y == 3 :> {a, b}]$

Out[12]=

Options (8)

Heads (1)

Ignore heads:

In[13]:=

Out[13]=

Mode (1)

Change the mode of matching multiple subexpressions:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

In[17]:=

Out[17]=

Method (2)

Three substitution strategies are supported, based on the direction of pattern unification:

In[18]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[a, b], f[y_, x_], f[a, x_]}, f[z_, b] -> c, 1, Method -> "Substitution"]$

Out[18]=

In[19]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[a, b], f[y_, x_], f[a, x_]}, f[z_, b] -> c, 1, Method -> "Cosubstitution"]$

Out[19]=

In[20]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[a, b], f[y_, x_], f[a, x_]}, f[z_, b] -> c, 1, Method -> "Bisubstitution"]$

Out[20]=

Get all tuple bisubstitutions:

In[21]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[a, x_], f[b, y_], f[c, z_], g[x_, y_, z_]}, {f[u_, 1], f[v_, 2]} -> {u, v}, 1, Method -> "Bisubstitution"]$

Out[21]=

ReturnMatches (2)

Return corresponding matches only without performing a substitution (note the HoldForm wrapping of individual matched subexpressions to prevent evaluation):

In[22]:=

Out[22]=

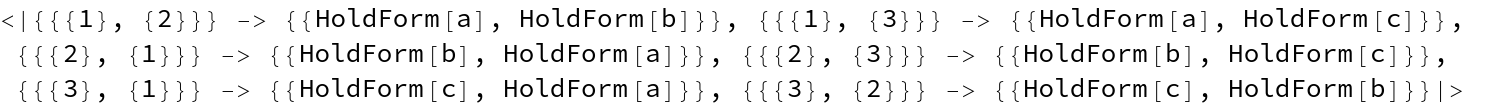This is equivalent to just dropping the right-hand side of a rule:

In[23]:=

Out[23]=

PatternSubstitutions (2)

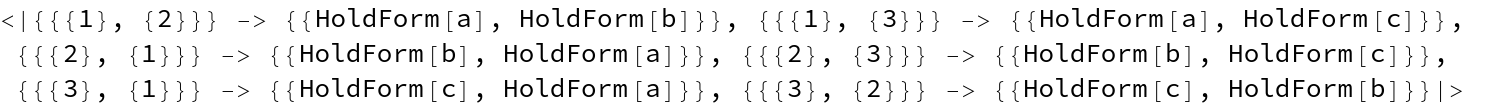Include all corresponding pattern substitutions:

In[24]:=

Out[24]=

"Cosubstitution" and "Bisubstitution" include substitutions of patterns from the expression to subexpressions from the left-hand side of the rule:

In[25]:=

Out[25]=

In[26]:=

Out[26]=

Properties and Relations (2)

Replacement is done in all possible ways similar to ReplaceList but at multiple positions:

In[27]:=

Out[27]=

In[28]:=

Out[28]=

SequenceReplace and SubsetReplace replace all the matches and destroy subexpressions, while MultiReplace does all possible single replacements and preserves subexpressions:

In[29]:=

$SequenceReplace[{a, b, x, x, a, c}, {a, e_} :> f[e]]$

Out[29]=

In[30]:=

$SubsetReplace[{a, b, x, x, a, c}, {a, e_} :> f[e]]$

Out[30]=

In[31]:=

$ResourceFunction[ "MultiReplace", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{a, b, x, x, a, c}, {a, e_} :> f[e]]$

Out[31]=

Requirements

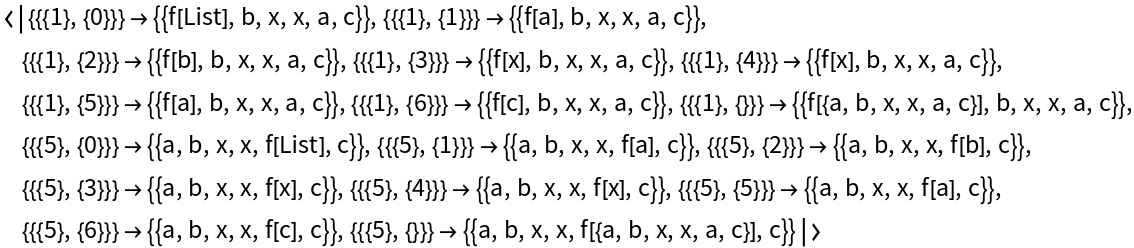Wolfram Language 13.0 (December 2021) or above

Version History

2.2.3 – 05 January 2024
2.2.2 – 27 September 2023
2.2.1 – 22 February 2023
2.2.0 – 03 February 2023
2.1.0 – 15 June 2022
2.0.0 – 01 February 2022
1.0.0 – 08 November 2021

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

MultiReplace

Details and Options