Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the moving orthonormal frame of a surface
ResourceFunction["MovingOrthonormalFrame"][x,{u,v}] computes the moving orthonormal frame of a parametrized 3D surface x with respect to variables u and v. |
Define the Chebyshev principal patch on the pseudosphere:
| In[1]:= |
The moving frame associated to a patch x:
| In[2]:= |
| Out[2]= |  |
| In[3]:= |
| Out[3]= |
Plot the moving frame as u and v are varied:
| In[4]:= | ![Manipulate[Show[ParametricPlot3D[
pseudospheretcheb[1][u, v], {u, -2.8, 2.8}, {v, 0, 3 (Pi/2)}, PlotStyle -> Opacity[0.5], PlotRange -> All], Graphics3D[
Arrow[{pseudospheretcheb[1][uf, vf], pseudospheretcheb[1][uf, vf] + #}] & /@ (mof /. {a -> 1, u -> uf, v -> vf})]], {{uf, 1.}, -2.8, 2.8}, {{vf, .35}, 0, 3 \[Pi]/2}]](https://www.wolframcloud.com/obj/resourcesystem/images/d43/d43ddaec-696e-40fd-9f93-677fcdf180ff/7911dcdb7a39f73b.png) |
| Out[4]= | 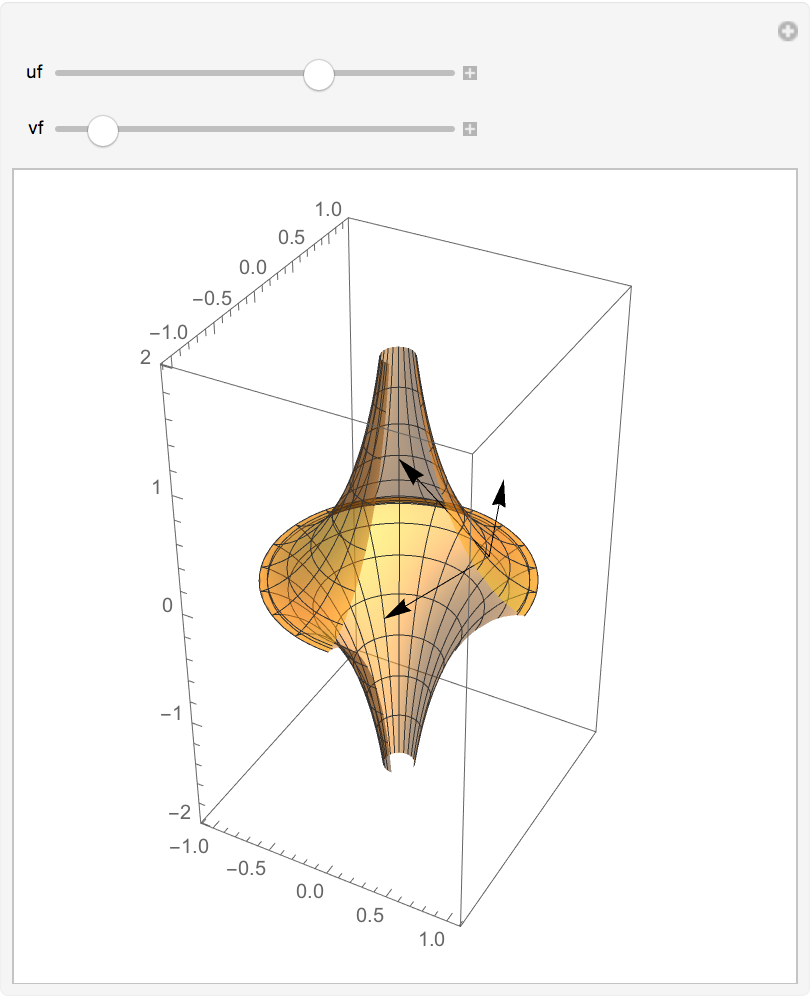 |
This work is licensed under a Creative Commons Attribution 4.0 International License