Basic Examples (1) 

Shuffle the list of integers up to 10:

In[1]:=

Out[1]=

Scope (3) 

Shuffle a list multiple times:

In[2]:=

Out[2]=

Confirm that this is the same as applying MongeanShuffle three times:

In[3]:=

Out[3]=

For different lengths of lists, different numbers of shuffles will return them to the original ordering:

In[4]:=

Out[4]=

In[5]:=

Out[5]=

In[6]:=

Out[6]=

Lists of odd length will take the same number of Monge’s shuffles to return to their original ordering as the list of even length preceding them:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

In[9]:=

Out[9]=

Properties and Relations (3) 

The following visualizes how the ordering of the list shifts:

In[10]:=

Out[11]=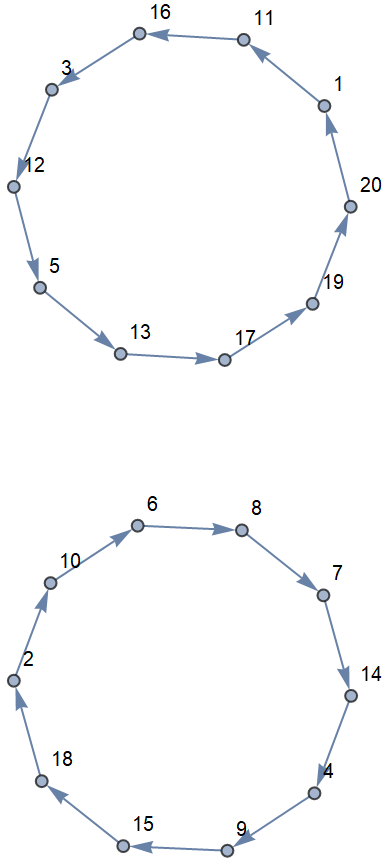

In[12]:=

Out[13]=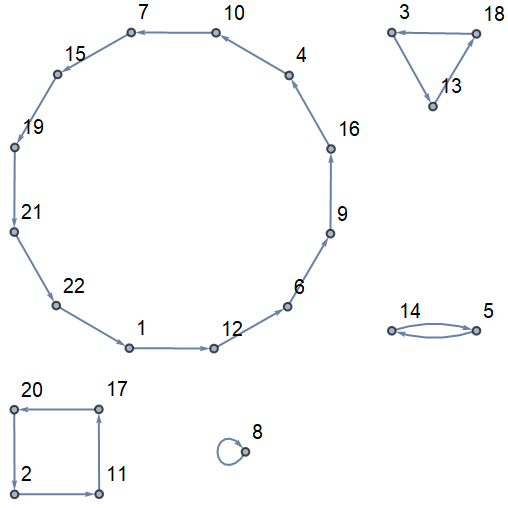

Visualize the recurring pattern when shuffling lists of different length:

In[14]:=

Out[14]=

Another way to visualize the movement of each item is through a simple ListPlot:

In[15]:=

Out[15]=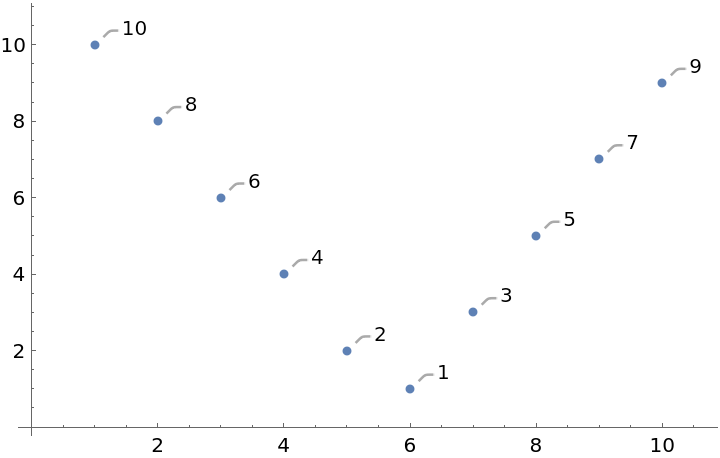

The same list shuffled with two iterations of MongeanShuffle:

In[16]:=

Out[16]=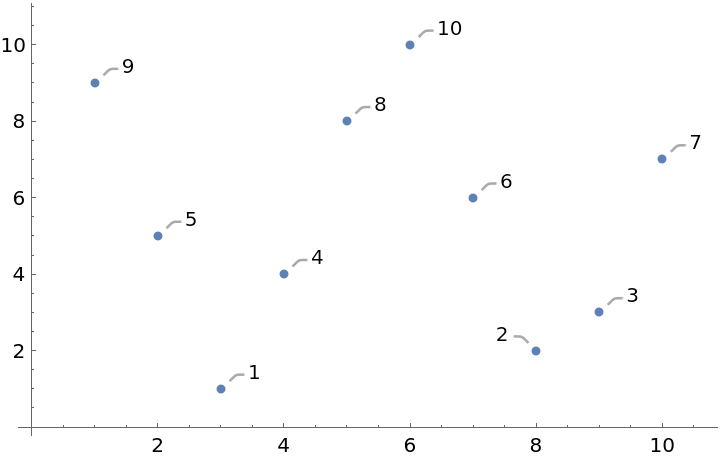

Neat Examples (2) 

Use ResourceFunction["PlayingCardGraphics"] to visualize a sorted deck of cards:

In[17]:=

Out[17]=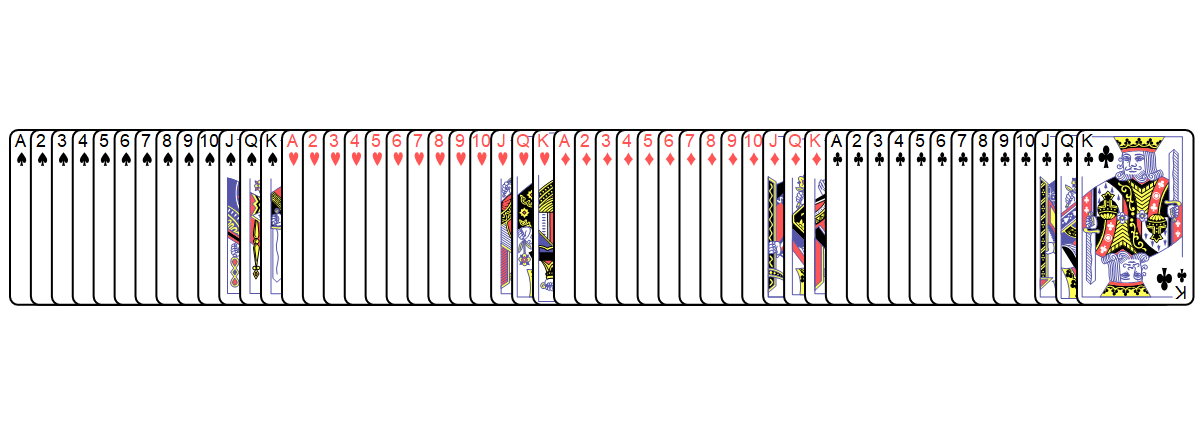

Shuffle the same deck of cards using two iterations of MongeanShuffle and visualize the result:

In[18]:=

Out[18]=