Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
This resource function is obsolete. Use the MoleculeValue built-in symbol instead.

Function Repository Resource:

 MolecularComplexity

Source Notebook

Compute the molecular complexity of a given molecule

Contributed by: William Borrelli

ResourceFunction["MolecularComplexity"][mol]

returns the molecular complexity Cm for Molecule mol.

ResourceFunction["MolecularComplexity"][str]

returns the molecular complexity for the input molecule identifier str.

Details and Options

ResourceFunction["MolecularComplexity"] uses Böttcher's definition, which takes the following form , where Vi is the number of valence electrons, bi is the total number of bonds to any atom with Vibi>1, di is the number of chemically nonequivalent bonds to atoms with Vibi>1, ei is the number of different atoms in atom i's microenvironment and si is the number of possible isomeric structures at position i.
ResourceFunction["MolecularComplexity"] will return an error for 0 complexity entities or entities that cannot be recognized as a molecule by Molecule.
ResourceFunction["MolecularComplexity"] utilizes MoleculeValue's equivalent atoms, which may differ slightly from true chemical equivalence.
ResourceFunction["MolecularComplexity"] takes the option "Stereochemistry", which changes how equivalent atoms and groups are defined. When set to False, this changes how diastereotopic groups and some corresponding ring atoms are considered equivalent or nonequivalent.

Examples

Basic Examples (2) 

A molecule identifier readable by Molecule or a Molecule object itself can be taken as input. By default, it returns a numerical output corresponding to the Cm of the molecule:

In[1]:=
ResourceFunction["MolecularComplexity"]["tert-butyl acetate"]
Out[1]=

Use a Molecule as input:

In[2]:=
m = Molecule["R-2-bromobutane"]
Out[2]=
In[3]:=
ResourceFunction["MolecularComplexity"][m]
Out[3]=

Scope (2) 

MolecularComplexity accepts a SMILES or InChI string argument:

In[4]:=
ResourceFunction["MolecularComplexity"]["c1ccccc1"]
Out[4]=
In[5]:=
ResourceFunction[ "MolecularComplexity"]["InChI=1S/C6H6/c1-2-4-6-5-3-1/h1-6H"]
Out[5]=

MolecularComplexity threads over lists:

In[6]:=
ResourceFunction[ "MolecularComplexity"][{"benzene", "hexane", "propane"}]
Out[6]=

Options (2) 

Stereochemistry (2) 

With "Stereochemistry"→True, MolecularComplexity considers stereochemistry:

In[7]:=
ResourceFunction["MolecularComplexity"]["2,3-dimethylpentane"]
Out[7]=
In[8]:=
ResourceFunction["MolecularComplexity"]["2,3-dimethylpentane", "Stereochemistry" -> True]
Out[8]=

With "Stereochemistry"→False, you can force MolecularComplexity to not account for diastereotopic groups:

In[9]:=
ResourceFunction["MolecularComplexity"]["2,3-dimethylpentane", "Stereochemistry" -> False]
Out[9]=

Possible Issues (2) 

Zero complexity inputs return an error:

In[10]:=
ResourceFunction["MolecularComplexity"]["methane"]
Out[10]=
In[11]:=
ResourceFunction["MolecularComplexity"]["[Na+]"]
Out[11]=

MolecularComplexity utilizes Molecule options, so it can only take identifiers that Molecule can parse:

In[12]:=
ResourceFunction["MolecularComplexity"][Molecule["ethanol"]["InChI"]]
Out[12]=

Neat Examples (2) 

Show that the trend in molecular complexity of alkanes with increasing (CH2) groups from 1 to 10 is linear:

In[13]:=
complexities = ResourceFunction[ "MolecularComplexity"] /@ {"propane", "butane", "pentane", "hexane", "heptane", "octane", "nonane", "decane", "undecane", "dodecane"};
In[14]:=
Show[ListPlot[Thread[{Range[1, 10], complexities}], AxesLabel -> {"\!\(\*SubscriptBox[\(CH\), \(2\)]\) groups (n)", "\!\(\*SubscriptBox[\(C\), \(m\)]\)/mcbit"}, PlotStyle -> Black], Plot[Evaluate[ Fit[Thread[{Range[1, 10], complexities}], {1, x}, x]], {x, 1, 10}, PlotStyle -> {Red, Dashed}], ImageSize -> Large]
Out[14]=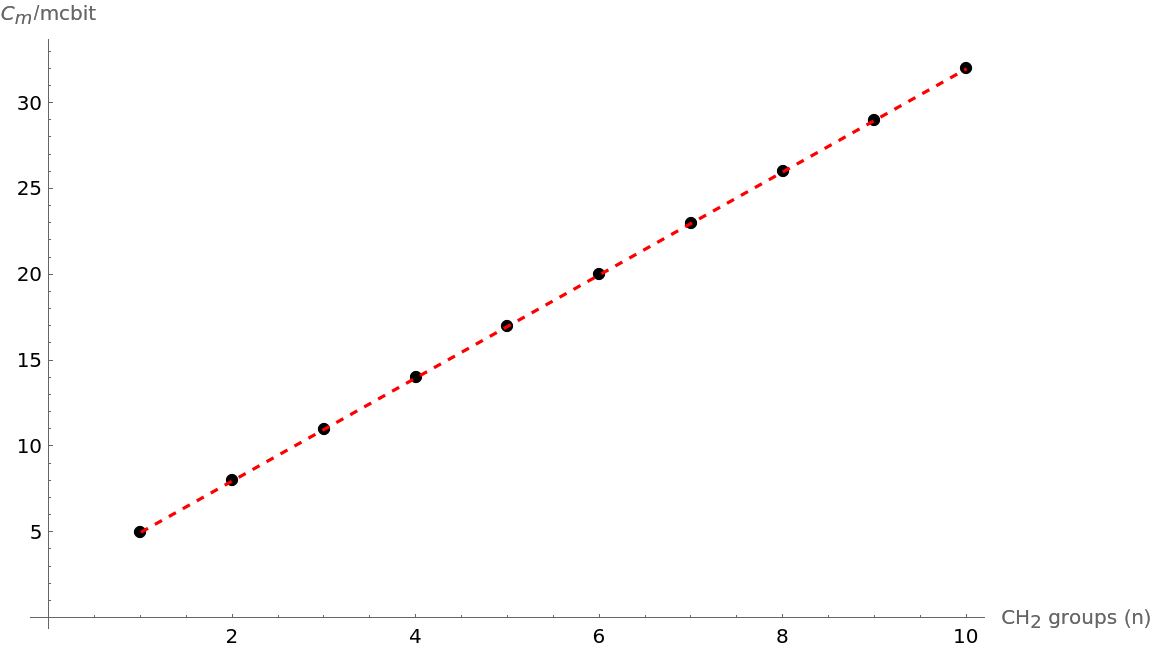

Calculate the change in complexity for a Diels–Alder reaction:

In[15]:=
(* define the reactants and product *) butadiene = Molecule["1,3-butadiene"]; ethene = Molecule["ethene"]; cyclohexene = Molecule["cyclohexene"];
In[16]:=
(* compute the complexities and find the difference *) cButadiene = ResourceFunction["MolecularComplexity"][butadiene]; cEthene = ResourceFunction["MolecularComplexity"][ethene]; cCyclohexene = ResourceFunction["MolecularComplexity"][cyclohexene];
In[17]:=
cDiff = cCyclohexene - (cButadiene + cEthene);
In[18]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/56784de3-8455-442e-997c-6dcfd8368fff"]
Out[18]=

Publisher

Will Borrelli

Version History

  • 1.0.0 – 03 March 2021

Source Metadata

License Information