Basic Examples (6)
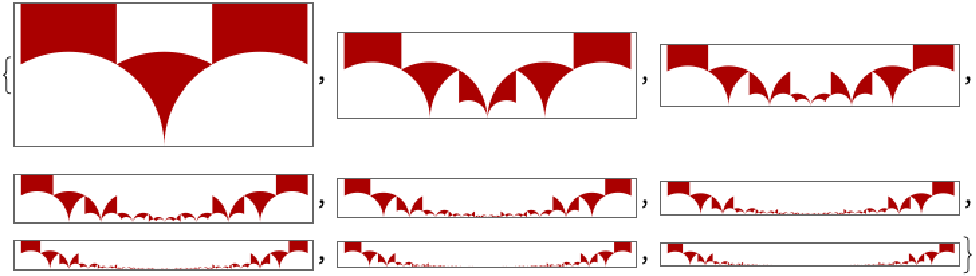
Plot the first few iterations of applying the generators of the modular group with alternating black and white colors:
The polygons of the first two orders of the tessellations:
The bounding circles of the first orders:
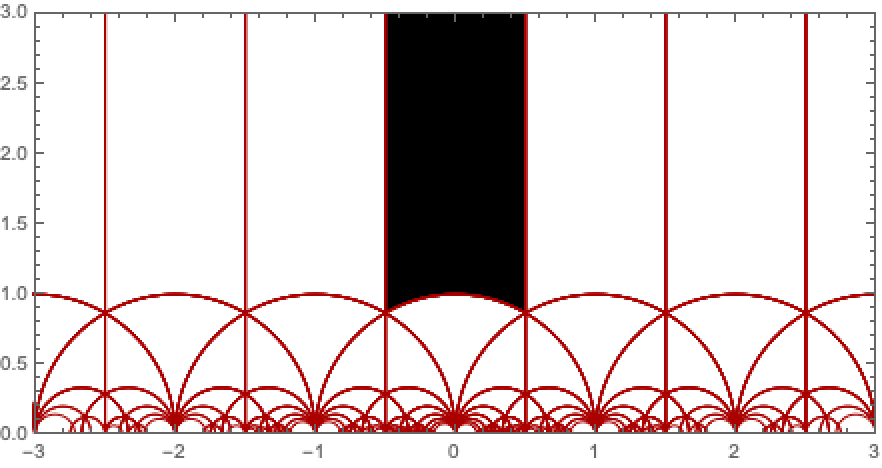
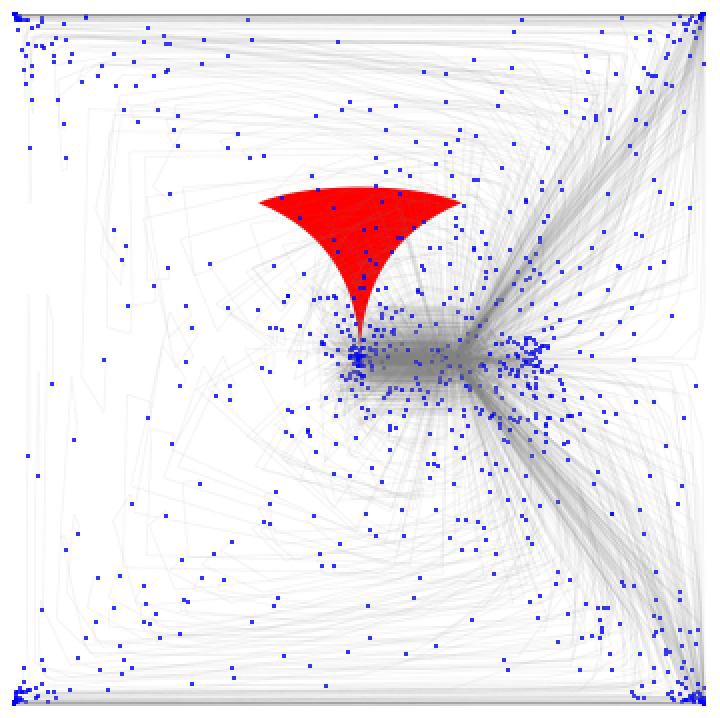
Show the fundamental domain and the boundary circles of the first order modular transformations:
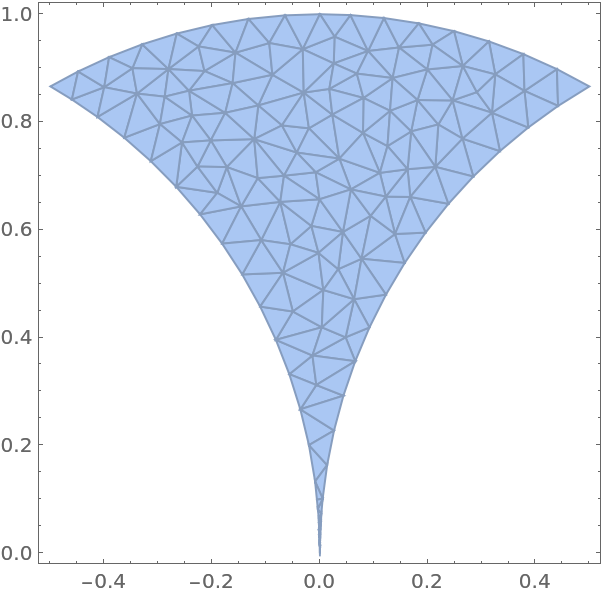
The mapped fundamental polygons of the upper half-plane conformally mapped into the unit disk:
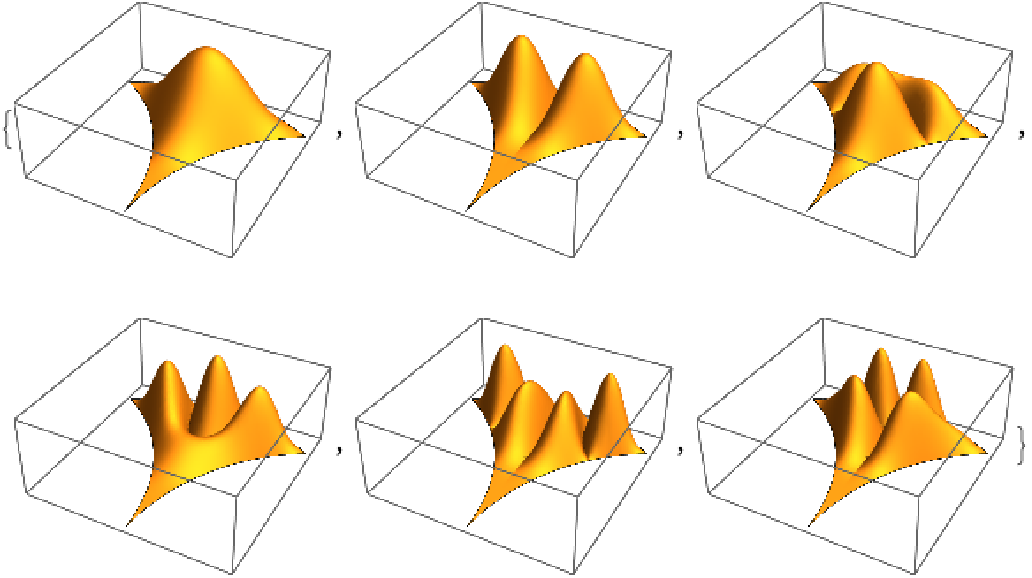
The polygons of the first eight orders of mapping the fundamental domain:
Scope (9)
Use the keys of the association to add tooltip labels to the mapped fundamental domain polygons:
Explicit exact form of the circles and lines bounding the curvilinear triangles of order 3:
Plot the bounding circles of curvilinear triangles:
The bounding circles of the first few orders of curvilinear triangle (the blue circles are overlaid over the polygons):
The curvilinear triangles and vertical stripes as Boolean regions:
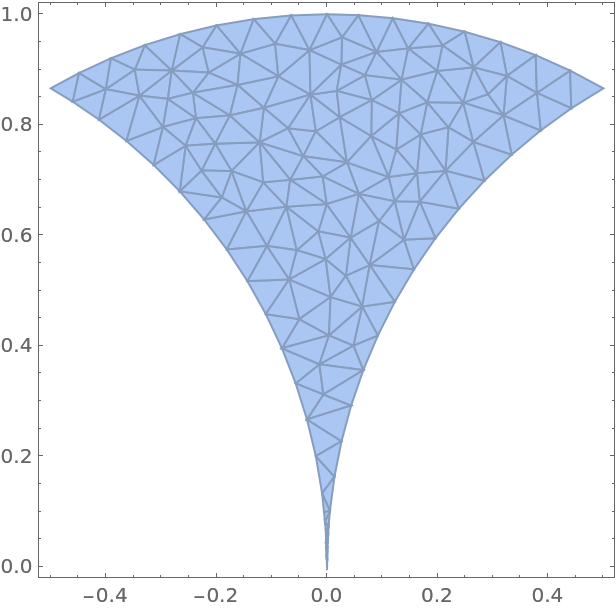
Discretize one of the regions:
The curvilinear triangles and vertical stripes as implicit regions:
Discretize one of the regions:
Compute the area of one of these regions exactly:
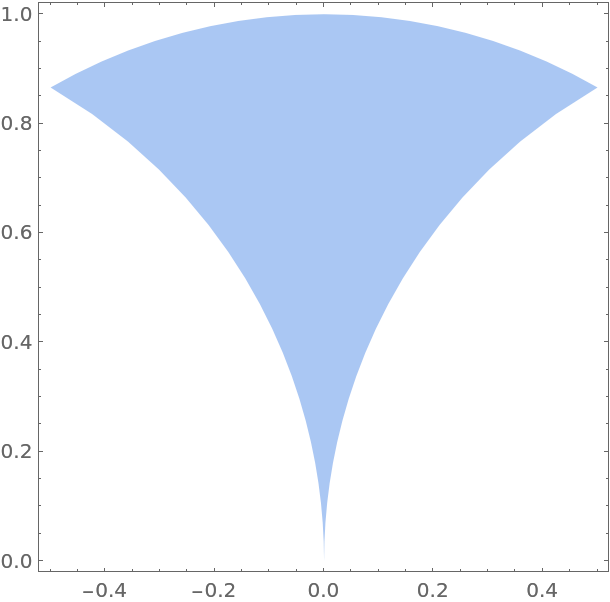
Compute the perimeter of the map of the fundamental domain under 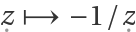 :
:
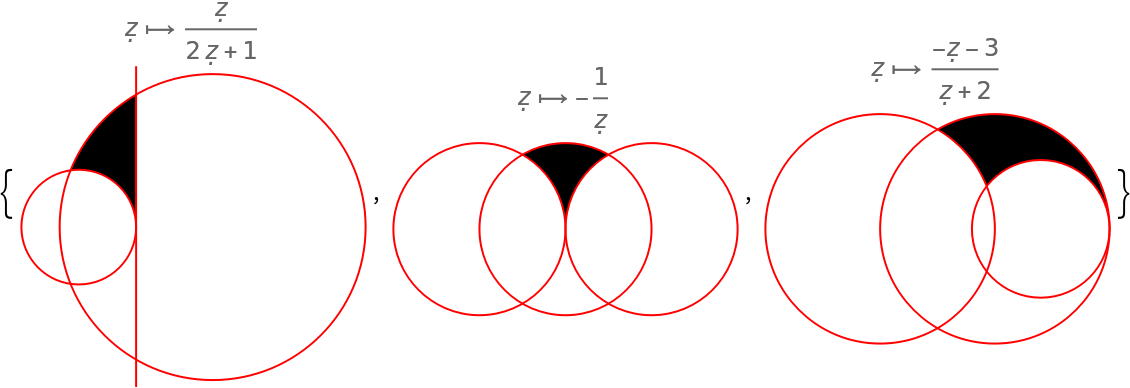
The modular transformations of the first few orders:
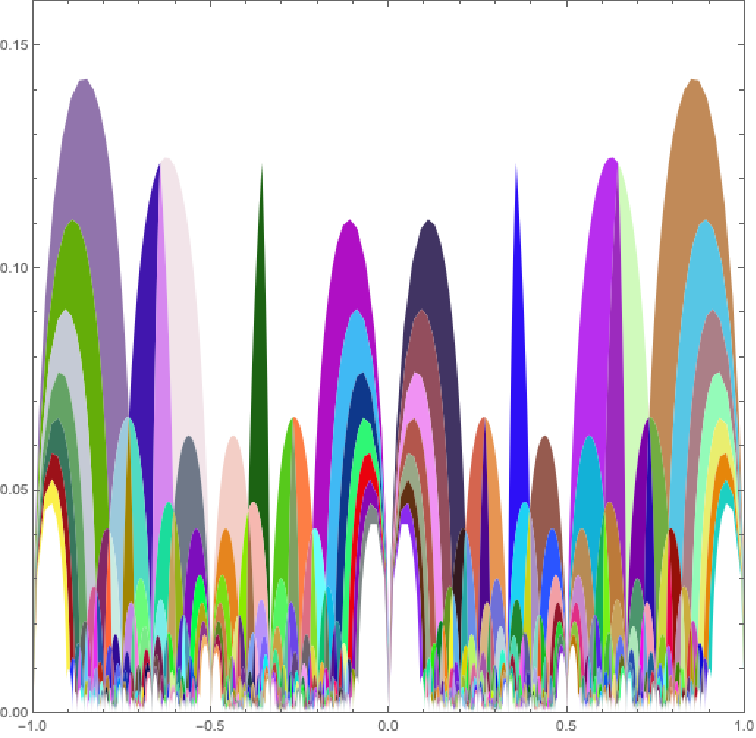
Show curvilinear triangles from a range of orders (here from 6 to 12):
Options (4)
By default, the translations of the fundamental domains extending to  are included:
are included:
Do not include the vertical stripe polygons:
Include the vertical stripe polygons, but cut them at 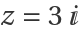 :
:
Vary the number of points along the boundary segments of the fundamental domain and its mappings:
Applications (7)
Calculate the areas of the curvilinear triangles of order 5 (the vertical stripes generated by 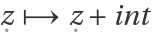 have infinite area):
have infinite area):
Compute the eigenvalues of the Laplacian (with appropriate metric factor 1/y2) for the map of the fundamental domain under the modular transformation 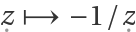 :
:
The region the eigenvalue problem is to be solved in:
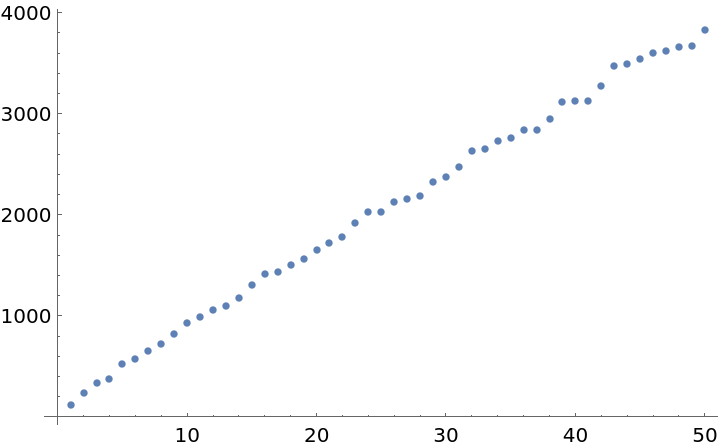
Plot the values of the first 50 eigenvalues:
Plot the eigenfunctions of the first six eigenfunctions:
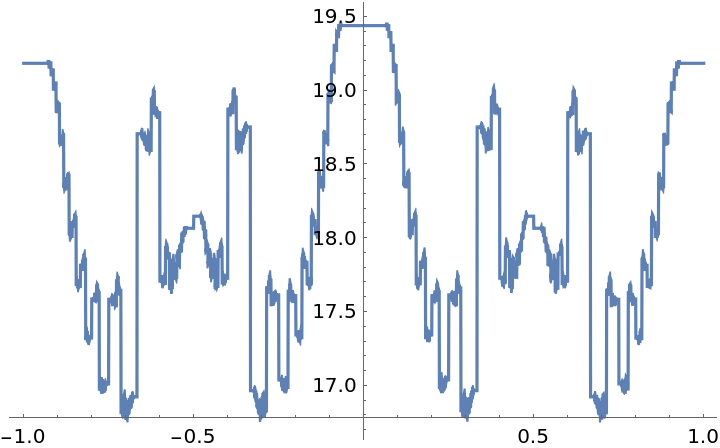
A contour plot of a higher eigenstate:
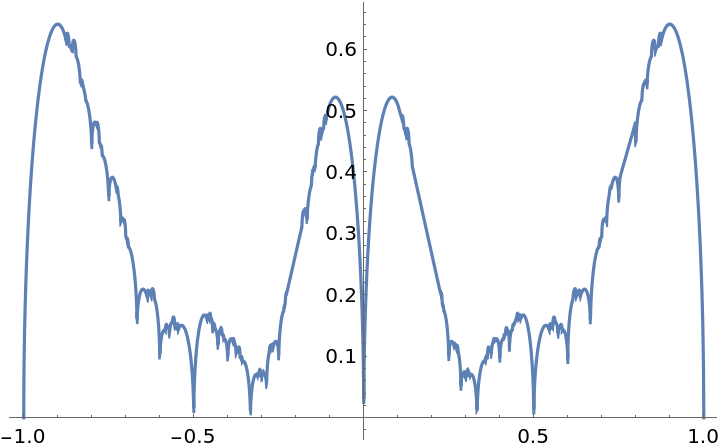
Compare the shape of the curvilinear triangles. To compare triangles of different size, rescale all triangles to have the same horizontal extension:
Show all triangles of the order 16:
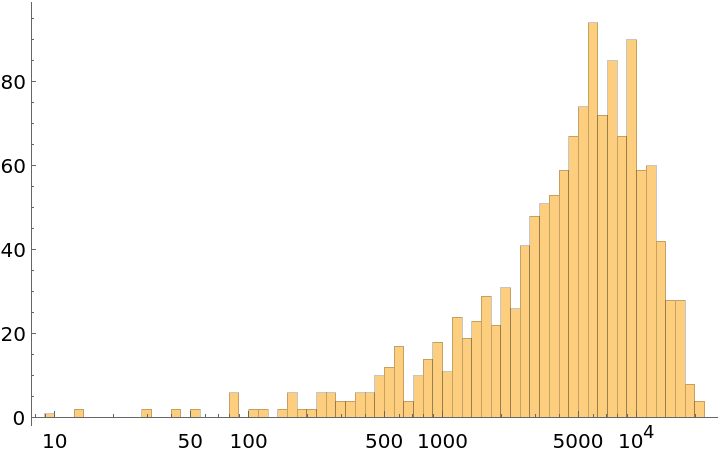
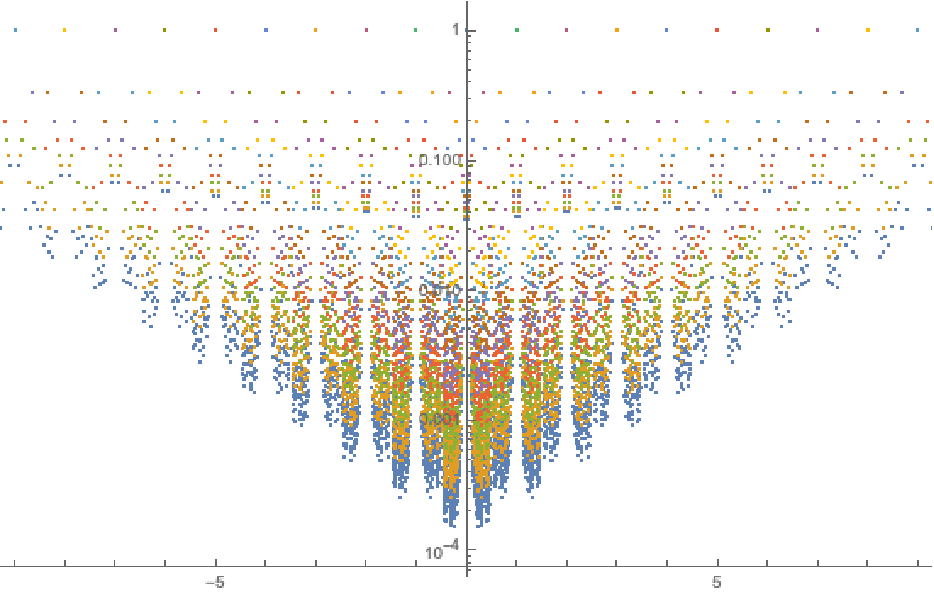
The radii distribution of the circles of the first 18 orders:
Plot the sum of the radii of the first 16 orders of circles:
Add the local heights of the order 10 circles:
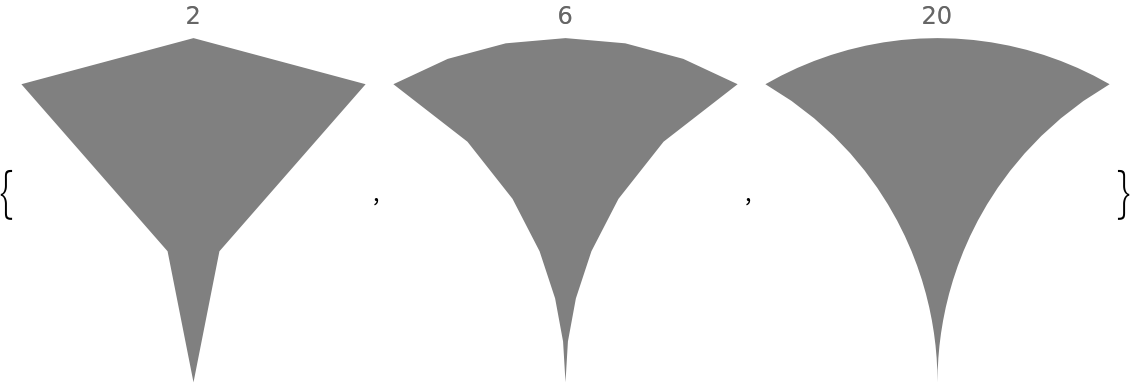
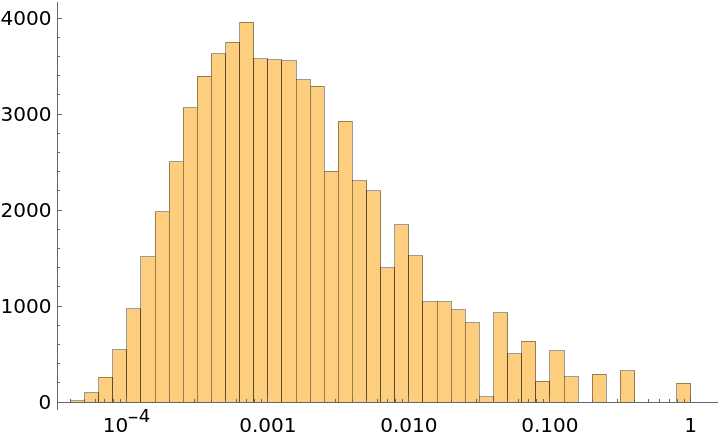
The size of the triangles varies substantially within a given order. Plot a histogram of all finite order 16 triangles:
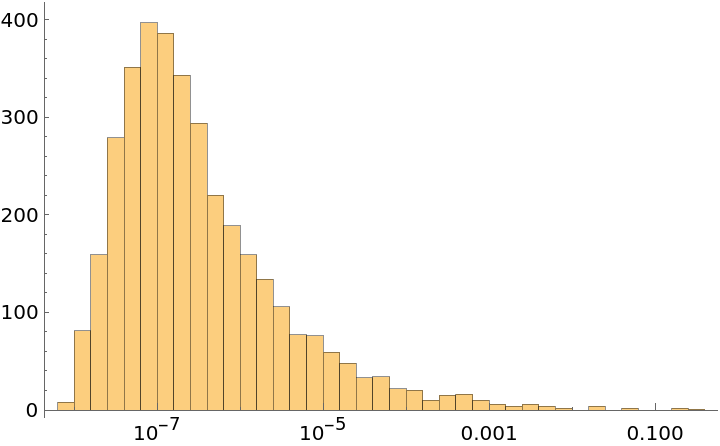
Plot a histogram of the distribution of the perimeter-to-area values for the order 14 triangles:
Properties and Relations (7)
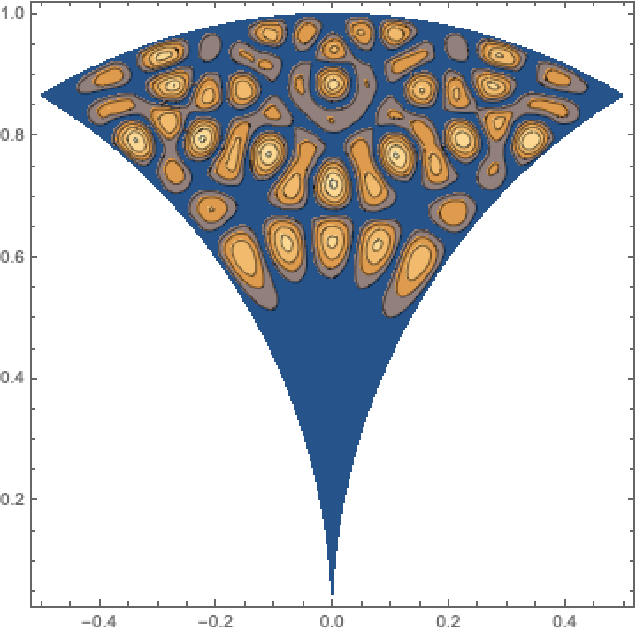
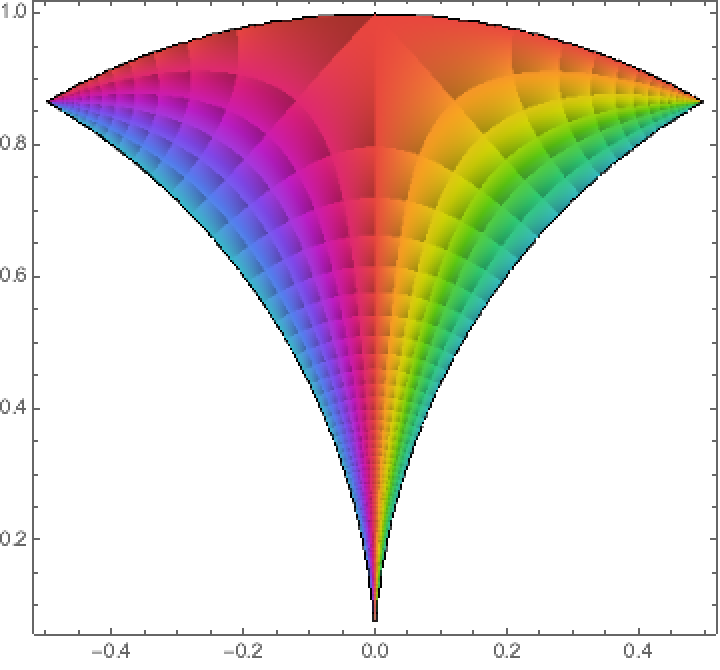
The Klein invariant takes on every complex value within each of the mapped fundamental domains. Plot the Klein invariant over one of the triangles:
The Klein invariant obeys J(z)=J(f(z)) for any modular transform f. Check this for the first three orders to 50 digits:
Use the Fourier series of the Klein invariant to visualize the mapping from a fundamental triangle to the complex plane:
Use an arctan transformation to map the infinite plane into a finite square:
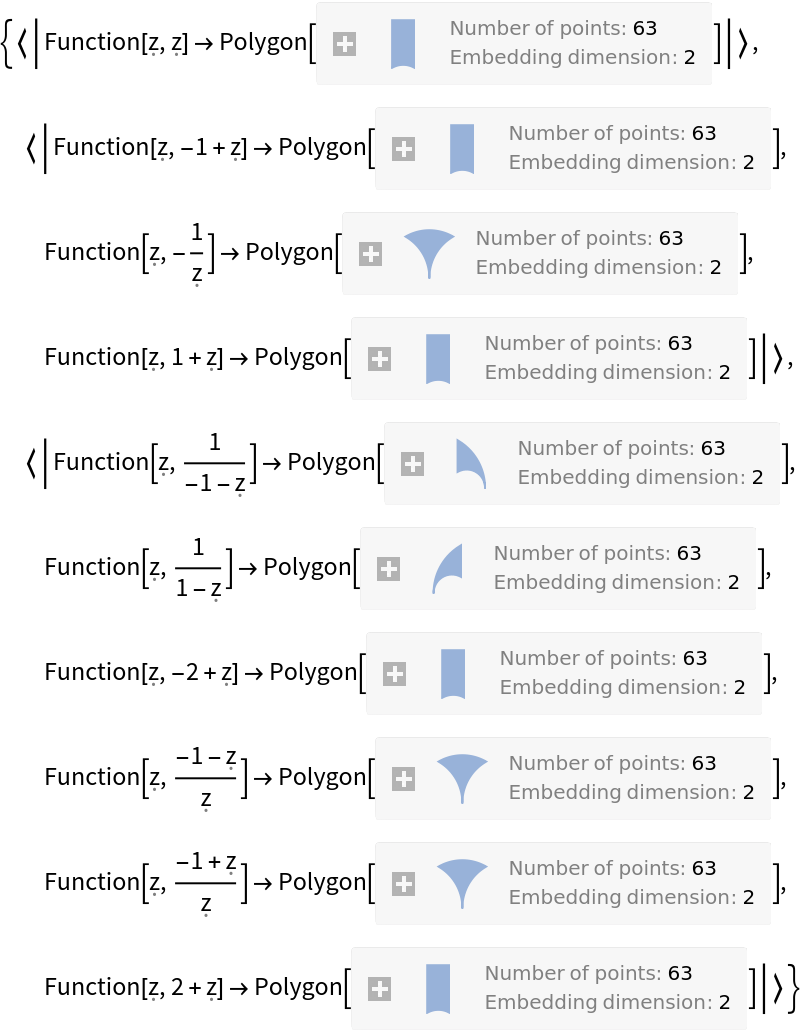
A given modular transform can be represented in multiple ways. Here are all possibilities with up to three generator applications (for easier readability we abbreviate the pure functions of the generators):
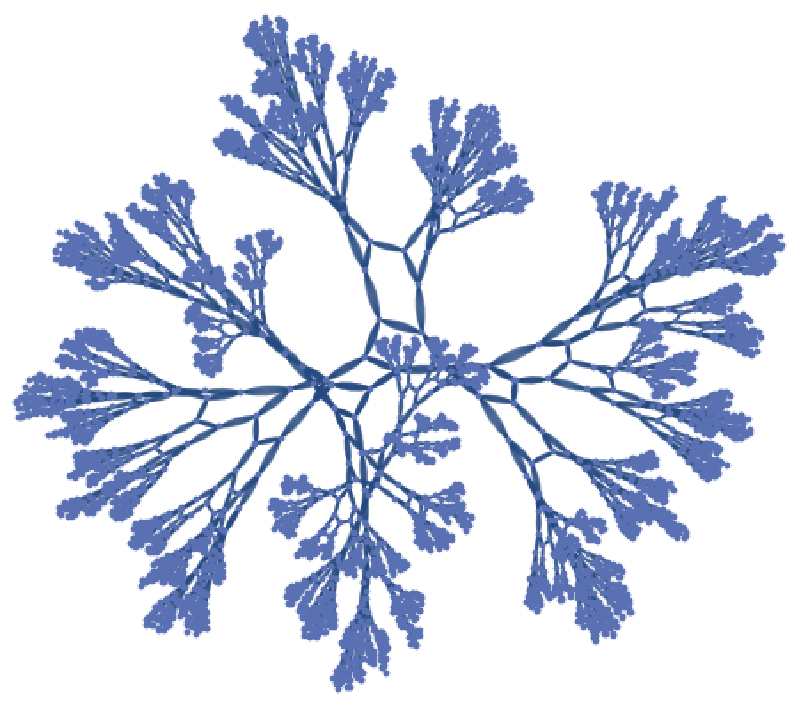
Show the network of modular transforms by connecting transforms that arise from applying a generator:
Plot the circle radii for the first 16 orders on a logarithmic scale (each order adds two circles of radius 1 and near the origin more and more small circles are generated):
Place the circles in 3D with smaller circles placed in front of larger ones:
Plot Ford circles (arising from the Farey sequence) together with the circles from the modular tessellation:
Possible Issues (3)
The number of modular transformations increases quickly with the order. This means graphics of order ≃20 will take longer to compute and render:
The polygons are approximate; this means making their boundaries near the x-axis visible by using logarithmic scaling shows numerical artifacts:
Boolean regions, implicit regions and bounding circles are only supported for the upper half-plane, not for the unit circle–mapped triangles:
Neat Examples (7)
A symmetrized version of the modular tessellation:
Color each order of triangles differently:
Convert each triangle into a 3D plot with the height depending on the distance to the polygon boundary:
Conformally map the triangles of the unit disk into a triangle:
Interactively change the parameters of the most general map from the upper half-plane to the unit disk:
Map an interactively movable point from the fundamental domain into other triangles and connect nearest points by lines:
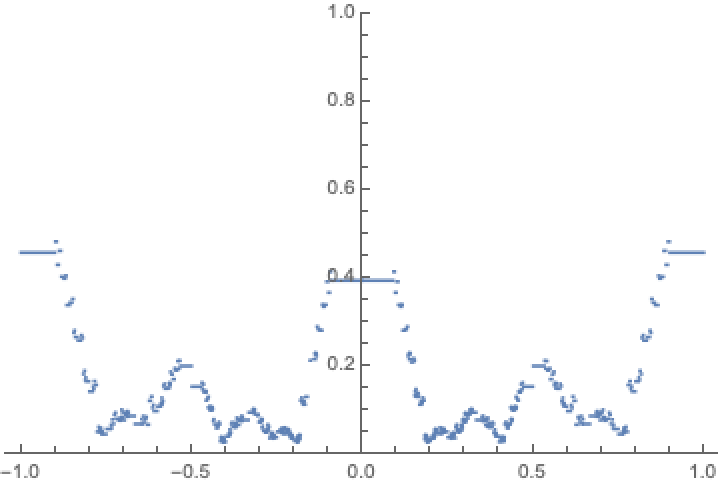
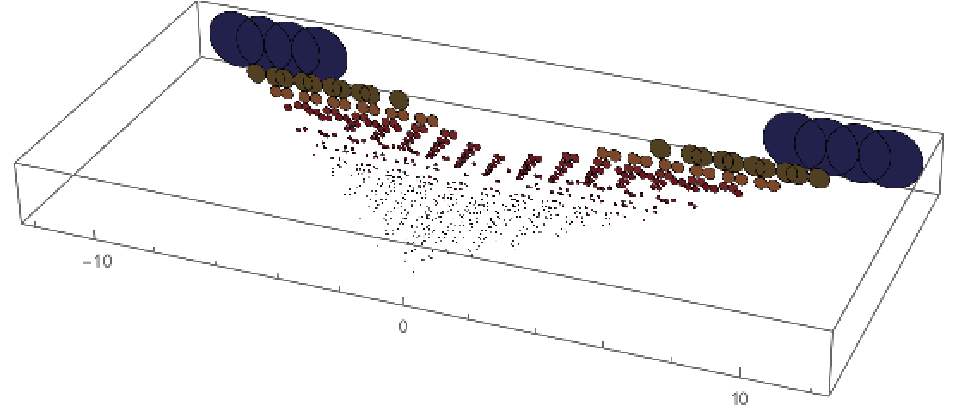
Extract the circles of order 12 and locally add their radii:
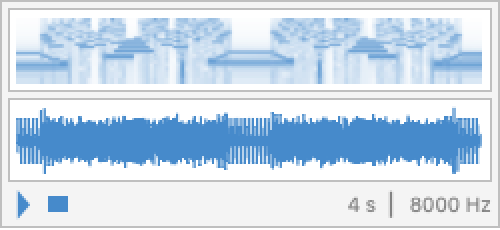
Associate a frequency proportional to the circle's curvatures and play the resulting sound:
![Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, ResourceFunction["ModularTessellation"][8] ], PlotRange -> {{0, 2}, {0, 3/2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/63df468e615e29c6.png)


![Graphics[{Darker[Blue], Values @ ResourceFunction["ModularTessellation"][8, "BoundingCircles"]},
PlotRange -> 3/2]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/46fc4a50366b2453.png)
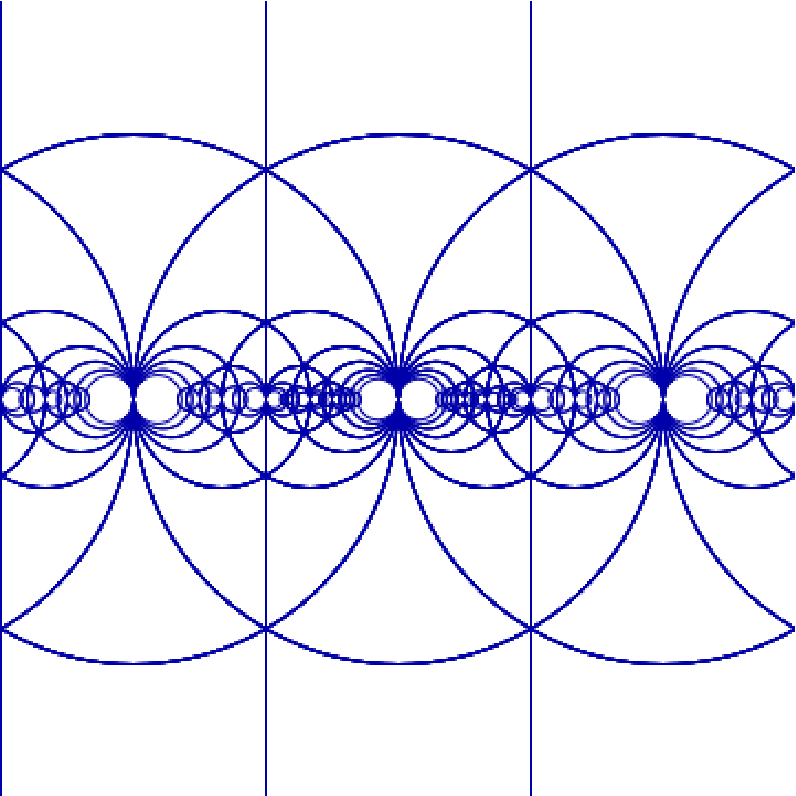
![Graphics[{ResourceFunction["ModularTessellation"][0], Darker[Red], Values[ResourceFunction["ModularTessellation"][8, "BoundingCircles"]]},
PlotRange -> { {-3, 3}, {0, 3}} , Frame -> True, PlotRangeClipping -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/191e7e018a2f7500.png)
![Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, Values @ ResourceFunction["ModularTessellation"][
10, {"UnitDiskMappedApproximationPolygons", {I, -Pi/2}}] ],
PlotRange -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/21b37aa432d7c504.png)

![Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, KeyValueMap[
Mouseover[#2, {Red, Reverse[Tooltip[##]]}] &, #] & /@
ResourceFunction["ModularTessellation"][6, "ApproximationPolygons"]], PlotRange -> {{0, 2}, {0, 3/2}}] // TraditionalForm](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/071b5fe280cfc04d.png)
![\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzsnQV8E+cbx5MU2kIprFBKseEUHTJsUGBDBwwYY2y4+2DrcPgzbIyhY7gM
dxsyZLgMd6dAi7W0VKDUS/X+v9y112tySS7J5S7y/j6hn5Bc3nvtvu/zvFqm
/0/fDFYpFIrRrvjzTb/xX4wa1W9i54/wny4/jh425MdBA9v8OGbQkEGjGvR3
wodNlQrFJfxTv6eIJNd///2nICKysFDN5K7pRERSiBCVSAIRohI5iAhRiSQQ
ISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCV
SAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmI
CFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEq
kYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgC
EaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhR
iSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGD
iBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGi
EjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkk
ECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQ
lUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5
iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAh
KpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVI
AhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgI
UYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqR
g4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIR
ohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJ
JBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOI
EJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQISqRg4gQlUgCEaIS
OYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCVSAIRohI5iAhRiSQQ
ISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGiEjmICFGJJBAhKpGDiBCV
SAIRohI5iAhRiSQQISqRg4gQlUgCEaISOYgIUYkkECEqkYOIEJVIAhGi2qhC
Q0ODg4PfvHkTFhYWERERGRn59u3bd+/eRUVFvX//Pjo6OiYmJjY2Ni4uLjEx
MTk5OTU1NT09PYOW3HGXR45JVCUtlUqVO3duV1dXNze3fPnyubu7FyhQoFCh
Ql5eXkVoeXt7F6NVgtbHWmI+Z67xpoVf4ecIBEEhQASLwHEL3Ai3Y+4rd+pl
kGMSlQFLWlpaSkrKhw8fwJz4+HjwByAClICmSFogVXh4OJAFcIFgIbSsgUgg
ZKNGjSpXrlyvXr2mTZt++eWXX3/9ddeuXfv06TN48OAffvjBz89v/Pjx06ZN
mzVr1tq1a//555/z58/fvn37wYMHT548ef36NZKGlIK9QC5CQ1aAt3Iny7Ky
b6ICX05OTqBZ3rx5gTgPD4/ChQuXLl26YsWKqCc1atRAJenVq9eIESPGjRv3
v//9b86cOdu2bTt+/Pi5c+cuX7588+bNu3fvPnz48PHjxwEBAc+ePXv+/PkL
WniD/+JDfIULcBkuxk/wQ/wcgSAoBIhgEThugRvVrFkTN8WtEQFEA5FBlBAx
RA+RtG/S2jdRQT+AAsRISEiAzQaGgCTgCSoJqseNGzdOnTq1d+/eDRs2LFq0
6Ndffx09enT//v27devWuXPn9u3bt27dulmzZr6+vvXr169Vq1aVKlVq164N
CsmdLAqtAEwF4aXs4uICE+Kjjz4qWLBg8eLF69Sp06ZNm549ew4bNmz+/Pn7
9++/ePEinhTkDGPronFJSkpCc2MNzYdYsieiMvCETQhYwUqEuQiCffrpp6iu
wNrcuXNXrFhx+PDhR48eMa0nKi0KVJp8xo1wO+ZBQwQQDUQGUULEED1EElFF
hBFtRB5JYDArd46KJnsiKgwtwBPWJgoUZIBh+fTpU7SnR44cWbVq1eTJk0FL
kAQ8qVChAhwWtt0Unl3gErAsd0LVRIUjJlYdyJUrF5ALW6JBgwZoR9CgTJ06
devWrSdOnEC7AysdSUaThJvatB1r00RlygjOtaenJ3AELrVs2fLHH39Exd6+
fTvMxVevXqEdRP2XO5v1CdFDJBFVRBjRRuSRBCQEyUGikDQkEMlEYuXOb9Nl
u0SF+ZSamooGEcYnzCo0iLA54d4uWLAAxQQjs3HjxiAnsGkUM/ULZp79EVWX
YDkgA5s2bdqvX79ly5b9/fffd+7cCQ0NRW7HxcUh520LsLZFVJVKlSdPnvz5
86Pphz/SpEmTb7/9dtKkSXv27Dl//jyaOdvKfD1CQpAcJApJQwKRTCQWSUbC
kXxkArJC7tIwQrZFVCA0MTERJiiK4NmzZ2jptmzZMmXKFJQCLE80c5bOLoci
qrZKlChRo0YN5PasWbOQ8w8ePAgLC4uOjkahWP8Dbv1ERRPG9IJ6e3vXqlWr
T58+yGd4Cvfu3UMmy51/0gmJRZKRcCS/d+/eyApkCONRWn//gPUTFRSFIx8V
FQUr9MKFC6tXr/bz82vVqpWPjw8yWeLscnCiagiGRMOGDcePH79+/frbt2+H
hISgmBISEtLS0uTOIR5ZJ1GBCKY7FAUK53fIkCF//PHH9evXYTPInWHWImQF
MgTZgsxBFiGjmA5Y66SrFRIV7nxKSgr8SniXz58/P3PmzJIlSwYMGADrCDkp
b3YRouoScqZevXooppUrV16+fDk4OBh0taquV+shKtxYFxcXVOaSJUt+9tln
o0aNWrt2raMZoqaJMV+RXcg0ZB0yENmIzLSengHrISoMG5g3oGhAQMDRo0d/
++23Ll26VKpUCY2R3JmULUJUIcqTJw/oOmzYsD179vj7+0dGRqJk4WvIm2my
EzVXrlzwWz09PatUqfLNN98sX778xo0biYmJ8maL7QpZhwxENiIzkaXIWGSv
7KNashMV5mhsbCwMe2QOPPoePXpUrFjR2dlZ3mzRJUJUY1WuXLnOnTuvWLHi
0qVLYWFhMo5Hy0VUVGZ3d/ciRYo0bNhw6NChu3fvfvbsmSw5YMdCliJjkb3I
ZGQ1MlwuhshCVPj1zKQ1+IYnTpyYOXNmy5Ytvby8ZMkBo0SIarJgQvj6+k6f
Pv3QoUNBQUFw3yRGq8REzZ07d/78+YsXL/7VV19NmTLl3Llz8L+kTK9jCpmM
rJ46dSqyHZmPIhBxqo8QSUlUBqQgEjzBHTt2jBw5slatWjDUpUyvmSJENV+u
rq7w0X7++ecjR468fv06JiZGmg4BaYjq5OQEA8nb27tFixazZ8++e/cuCkuC
1BFpCNmOzEcRoCBQHCgUaUaypCEqrJGoqKjnz59v27atb9++pUqVstGVaISo
IsrFxaVOnToTJkyAUREeHh4XF2fRSQIWJSozZA8/67PPPps2bdrly5cTEhIs
lxYi4UJBoDjgHKFoUECWniRgUaKmpKTAAoGLt3///mHDhvn4+FjPkJxpIkS1
hOCnNGvWDObEtWvXIiIi8AhYYvWrJYgKwyBPnjyenp7wtvz8/I4dO4YKL3rM
iUQRigYFhGJCYaHIUHCWsOssQVRYGrA3wsLCTp8+DQvk008/lbgrw3IiRLWo
UM/bt2+/atWqR48eRUdHi9sbIC5RYefkz5+/TJkyvXv33rNnD2q7iFElsqhQ
WCgyFByKD4UorskqLlHh3QM4N27cmDVrVpMmTaxq4pMoIkSVRuXKlYMtcebM
mcjISLG2+BCLqC4uLoUKFWrQoMGMGTMePnwoStyIZBGKD4WIokSBolhFqR6i
EBU+Gjy18PDwgwcP9u3bt2jRoqLEzQpFiCqlYD907Nhx8+bNr169gstmZi+r
mURVqVT58uUrVqxY586dt2zZAtSLVZpE8gpFiQJFsaJwUcRm9kyaSdSUlJT3
79/DR1uyZEnTpk3F4rzVihBVeimVymrVqv3yyy/wfZD5Js+5MpmouXPn9vDw
qFy58tixY69evYo6L25pElmDUKwoXBQxChrFbXJHpclETUxMjIiIOH369PDh
w8uUKWPa3W1OhKgyqnDhwj169Ni/fz+8IRO6AkwgqrOzM/zBZs2arVy5Migo
yBJFSWRtQkGjuFHoKHoTlgkYS1Q4+PHx8fDC1q9f365dO3d3d2PvaNMiRJVd
MB5atmy5efPmN2/eGLWE0yiiwtvy9PRs06bNjh07YmNjLVeURNYpFDqKHhUA
1cAo11s4UcHSuLi458+fw8GvV6+e8Y+CPYgQ1UqkVCqbNGmydu3a169fC5z5
KZCorq6uMIY7deq0b98+sujewYUKgGqAyoAqgYohpP4IIWp6ejqI/eTJk/nz
59eoUcO8R8G2RYhqbULjvnz58hcvXsB10j+L1SBR8+TJ4+Xl1b1792PHjln5
ZvhEUgqV4ejRo6gYqB6oJPprkX6igqUxMTEPHjyYOXNm5cqVxXsObFWEqNYp
NPR//vlnQEAA3ChdXNVD1Lx585YsWbJv375nz561nu0HiaxKqBioHqgkqCp6
1s7rIip+Hh0dffv27SlTppQtW9Yyz4HtiRDVmlWpUqXffvstMDCQtx+Al6gu
Li7e3t6DBg26fv269OVIZItCVUGFQbXh7V/VJiqaePj49+7dGzNmTIkSJSz/
HNiSCFGtX1WqVFm2bNnr16815gNoEDV37tyenp7ffvvtmTNnZCpGIhsWqg0q
D6qQxjwrDaKicYfrhIa+dOnSkj4GNiJCVFuRr6/v1q1bIyIi2B5Rlqi5cuXy
8PBo0aLF7t27ycZQRCYLlQdVCBUJ1Ynd6ZolKhp0NOto3D/55BP5ngNrFyGq
DQmVvH379ocPH0aRpaamoqqrVKr8+fM3aNBg7dq1ZE4UkShCRUJ1QqVC1VKq
VOf++y8lJSUyMnL79u2NGzeW+yGwdhGi2pxcXFz69Olz6dKlU6dO+fj4/P77
7zBc5S5AInsTKhWqVqVKPieOHTt69GiHDh1kP5/FJkSIaotydnauXbv2hg0b
YDbEx8fLXXpEdqqEhMC/d+9Zsri8j4/d7LZnaRGi2paUSmWBAgXatGkDG/Xs
2bOlS5deuHBhWFiY7McIEtmVUJ0iI6nlS6ny5dLPnDl2+nSzZs3UnQC2ua++
lCJEtSG5urpWqFBh/vz5TJcpOzL11Vdfga6kH5VIHMXFUZcvUp2/ppxUlEJB
nT+Pz96/fz9z5ky04FZ7CKmViBDVJqRSqTw8PL7//vtbt26xmcadPeXp6Tlt
2rSgoCCyNorIdKWkUCEh1OzfqKJF1CxlXpzZU5cvX+7YsSOgQYxVXSJEtX7l
zZu3WrVqa9as0dh2T3uGf+PGjQ8dOhQdHW2JQ1iI7FmoMDHR1PGjVMtmmSBV
KtUvtY2aYz5qUlLS4sWLfXx8DC5fdUwRolqznJycYHwOGjQoMDBQO9N410y5
u7v7+fkFBASIdVIAkf3rwwfq5Qtq/FjKo0AOnDJE5VuF+ujRo969excsWFCa
81htSISoVqt8+fLVr19/9+7dujJNz7r+GjVqbN26FSVLFvUT6ROqR1QUtXsX
VfdTTdNUL1EpekfrzZs316xZ0/7OijJHhKhWqNy5c3t5eY0bN07/8Xn6955y
cXHp16/fnTt3yKnQRPxKTKQe3KeGDqbc8tIIzWmaGiIqo1evXo0cORKeFJmt
yogQ1dqUP3/+L7744tixYwYzTcj+qOXKlVu5cmVkZCSZXkWUrbQ06u1bav0a
qkqlDA03X/1SZGS9Ycf69evAgQO+vr7wqiR4QKxchKjWI5imyIRff/31/fv3
QjJN4I7TSqWyc+fOly5dImsBiNRKiKeuX6N6dKWcnLRZyn2TkWmjGiYqRa+x
mjRpUrFixRzcWCVEtRLlzZu3RYsW165dE55pRp2KUrRo0fnz56OsyTQAxxWK
PiqKWrKYKlVSYwQqQ6mB1ixL1ZDXr6Fz5841adLEkacBEKLKLtiQKIURI0YY
uzzf2JP7cKO+ffs+f/6cHH7qiEpNpV69ooYOonLn0hzNz2Gd5jRWtWZPGVRo
aOiAAQMKFChgoefFykWIKq/gIpUuXXrZsmVpaWnGZpppp0s3bNjw7NmzZLjK
sZSYSF26SH3RVHNyFI+/n/NlpI3KCI/zggULSpQo4YBzqwhRZZSrq2v9+vXh
KJmWaaYRVUH3AKxevTo6OlrcQiSyUsVEUxvXU6VK5MSp1kQp8YjK6NixY7Vr
1zbq3FU7ECGqXMqfP3/v3r1fwREzVSYTVUGPgv3888/BwcEm2MZENiMUbmgo
NXE8lcfVADm1QWo2UaGAgIAuXbq4u7uL+OBYuQhRpZdKpfL29v7999/NXINv
DlEZMWNhZHWVferDB+rOLeqrtro9fc3BfZ4Phc2e0qOEhIQpU6YULlwY1V6U
x8fKRYgqseAEVatW7dChQ+ZnmvlEVdATVnfs2EH2rbI3xcVSe/dQlSrqxaky
c4qUFksz2L9mE5XR7t27fXx8HGHfKkJUKZUvX77OnTv7+/uLkmmiEBVyc3OD
FREeHk6WrNqDUIjvIqnfZlL58+dkqSJrThQPYDN0wdY8r5+r27dvt23b1u6X
rBKiSiOlUlmwYMEJEybExcWJlWliEZURUH///n2yGaBtKyWFevyI6tEtyzTl
mROlCU+DI1OGZk/pmuGs/XlUVJSfn5+Hh4cdbwZIiCqBcufOXb58+c2bN4ub
aeISFapevfrRo0fJ0ipbVUI8dfoUVbuW1ux9wQNS2u6/QpHx338ZNB65gjuT
YbwoOpxVq1aVKlXKXpdWEaJaWi4uLs2bN+fuFC2WRCcqBEN6/vz5ZGKV7Skm
Rr0YqkjhLJyqdLv5jKWqz3zNyHwpQNT0/86xRDUNpBpQhS5evOjr62uX3aqE
qBYVADVw4EALnVVqCaIq6E1ZEeeAgIAMsl7VJoRievGcGj4sczGUQtup566K
4h3c1wCp+pWuov+CqOcyiaqB03QB0riMDQSxDgoK6tOnD/hjiTosowhRLScv
L69Ro0ZZzt6zEFEZdenS5d69e2SsytqFAvJ/RPXqQam460mNWRXFxakq85XO
vqGJmq6+j8hC3CMjI0eMGFGoUCHLVWPpRYhqIZUoUWLGjBmJiYmWyzSLEhVq
3br19evXySYA1qvUVPWM047tDU6RMthfmmmRMlCl/6bT/9UmalqWUlNTmb+6
pP9bCMZqbGzshAkTvL29LVqTpRQhqiVUpkyZpUuXWnpLUksTFfL19T1z5gxZ
AmCN+vCBunCeaq4+FirDmKX6Gj2orFGaaZcqM9+rX0qVmqhnz6ap4S2+0FgD
qrA65syZYzePPyGquFIqlRUqVNi6dasEmSYBURX0BICDBw+SCQDWpcQE6ui/
VO2aJlinnKF/RXqWRZpplzKmKf0mTalKUypTFYrUM2dScxIVJGTfQMnJySlG
ivsTJqi//vqrbNmydjCrihBVRDk5OdWoUWP//v3SZJo0RIVQ1bdt20YmAFiL
YmOpPbspH/3roXhnTyk00Jqh5LCUwalC/TdVBZYyfxUpZ86k0KdKcWH4IUvw
X9g3rLS/4v7l/pcRY6zu2LGjcuXKtr5YlRBVLDk7Ozdo0ODUqVOSZZpkRIW8
vb1XrlxpDVXF0fU+itqwhvq4pPZ6qIzMMSmN0Xwds6fYjlOum682TZWpDFHx
Uipoop5Opp9QbXKKq/T09EOHDtWqVcump6oSoooiV1fXVq1a3bhxQ8pMk5Ko
CrqqzJ8/X/9hgkSWVUQEtWghVdiT59BSFqEaVivf7CmGpexoFOvsqxHK4FSp
TFEpk5XKZIUi6dTJJIpiuZdIKyEhgX0Tn1NxcXHsX+4nesSGBqiePn26cePG
trsHICGq+XJzc+vUqdPTp08lzjSJiaqgj26ZPHlycHCwxCklUivkNTV9GuWe
j28Hfg0T1MDWKNnD+jRL05xoT5/D0hSwlCZqEoh68kRiegYDT0ZxWoqNjdV4
w77nfqJ9vbZSU1Nv3rz55ZdforJJXL1FESGqmcqXL1+vXr1ev34tfaZJT1QF
vaJ2+PDhL1++lD69Dq3gIOrnnyhnZw2jNINrnRoY5c/eVyqd4/Uzr1T6laJU
qE1TlSLZSZmoUsapVHEKRezRo7HJydHR0e85ioqKYv6+o/X27dt3OcV+wrzh
vYD9eVSWmMAB7YcPH8JKscXzqghRzRGa0d69e0dGRsqSabIQVUHPZ+jfv39Q
UJAsqXZEob0ePpTv6FKljiWl+mZPZY7va+CUtktpnKpfiUrl28KF31SvHlK1
6ut//30dER6cpSBar2i9FEmvOGLCDw8Pv337docOHarQqlatWokSJWSp7caK
ENVkoQH97rvvZOxXlIuoChqqQ4cODQkJkSvtDqQ3byi/kSxOeQ8tFcZSZkBK
PVCVPQdVTVRFpoGqUr+SnJRJKmW0QvGqZ8/QK1dCTp8OCQwMCQ1FWb/WLZBW
1yfcrxgm6wkHYm8EqPr7+5+mdfHixSlTpshV240SIappcnV1hVcib4+ijERV
0FPFRo0a9QbPO5HlFB5OTRxH5XLSGmAyYIjyzp7KZGnOqafsyH4yjdNElSpJ
qYpUKJ6NG/s+IyMqLi6K9u619Z7vc+EfClF0dDTTuZqWlrZp0yYZa7twEaKa
IOAU/og5R0SJInmJqqAPcp00aRJsCXnzwW4VEUFN/UW77zTnFFPukJOCb1gq
e/ZU9mT+LH8/DQaqKtvZh3UKosarlCBq4OjRUR+S30krLk65nycmJq5bt07e
2i5QhKjGytnZuW3bts+fP5c7z+QnqoLeqxDumFw9yfasd2+pmTOoPHmMWRLF
N3sqm7GKDGVOnKrYAalsnMY5KeNUygiFImDM6PcfPlgIm6zVqvF5WFjYzZs3
r1y5AnOF+21CQsLmzZtt4qxqQlSjBKusRYsWYh1rYqasgagKuj/5999/t4Za
ZD96/55aMI9yczOMU+0LdPwkc4O+rCH+NA5Rk+m+0ySlMgFEVapinZRhIOpo
ixAVnHzz5k1QUBDTZcqdAxATE3PgwIGhQ4cOGzZs/vz53K9iY2MvXbr06aef
Wj9UCVGFC6Xp6+t79+5duXMrU1ZCVAU9heyPP/4gy1TFUWwMtWwxVYD3lCiN
jlNdm53y7X3K2akvh4Ga6e+rsgxUVYxS+SaTqOJ7/agkYOOmTZuWLl26ceNG
eDfsvCwQderUqVu3bj148GCjRo1evnyJD1kOvw5+Dd7Wrl3bypepEqIKFMqx
bt26ly9fljursmU9RIUKFCiwfPlyPBRy54qNKy6OWvcXVaigIetUY4W+4dlT
7BL+tCwblcXpB7WBqkpQqokKnL5XqUIUiqdjxrxPFp+oqCFnz56dPXt2gwYN
Ro8eDXv1Ba3nz5+HhoYGBgYCsLt37+7evXt4eDiXqMwFR44c+eSTT6x5QxVC
VCFCCdaqVQs1Qe58yiGrIipUqFChNWvWiHg0ocMpPp7aspHyLpI1ss8zLUrn
oaV6bdTMI07ov9lD/EwPqpPyg1KZCJyqVLEqNU7xClYonowZbQmiApJhYWHL
li0DTuH1w0RZvHgx7NUlS5bg+UpISECt7tGjx+HDh+Hps79iiArw4gJYqlWq
VJG7susUIaoQVa1a9fjx43JnkqasjahQ4cKF4dCh2sudNzaopERq5w6qeDH9
E6V4tz3RbaByRvmzZk+lqRTpKgXt9SuyxqRUCbTLHwOiOjlFOTmBqI/HjBLd
62c6UWGgdu7c+dq1a7BXr1y5sjpLly5dunXrVocOHebPn//s2TPYqNwfPqOF
N6hdf//9d4UKFeSu7PwiRDWoMmXK/PPPP3LnEI+skKhQsWLFUOHJzv/GKTWF
OvgPVeZjbWffoP2p39nn4JSz96kqe53Uh8wZU2qiRqtUwOk7leqVQuFvAaLC
7IRRCn9/zJgxy5cvByHxSQJHU6dObdKkya+//jpr1ix8y/X68d/AwMDIyEh8
mJSUtG3btpIlS8pd2XlEiKpfXl5eGzdulDt7+GWdRIV8fHzOnz9PDv4TKmTU
5UtUtSp8+50a2PaE1yLV+pAzbyqbqIrUrE7URCdVnFIZ66R2+aNUykgn5Us1
UcewY/3cYXftFfrCBRiCijt37ly4cOGJEyfg9bPMZLAJ3uLzf//9Fy4h91s1
UQOfBQQEgKhMOIDqokWLChYsKHdl1xQhqh65u7uj0bTa0+uslqhQ48aNrWSO
mQ0oMIBq0czQjlI6Xjyzp7SvybZU07WGpTKnoapUMXQPKgzUiFyqF2qiZs6e
As3u3Llz+vTpc+fOnTx58uHDhyzowDddgOVuhMJVXFzchQsXZs6cGR8fz8Up
I+6eVNyf4z1QzBAVwn+Za0aNGuXm5iZ3Zc8hQlRdypMnT79+/ax58NqaiQp1
69aNLPw3rDdvqP59clqnRozy833Ib9bmcPwZl58hqpLuRFWpO1GjnFTvnFQR
TqrnCsWjLKKCe0uXLh00aFCHDh2qV6++ZcsWoIwB3alTp16+fIlnhLstVXR0
ND65efMml71cNoaFhb148eK9AGkQ9cmTJ+Hh4QxRcZfExET8t2vXrla1mSoh
Kq+cnJzatWtn5bsrWzlRVSrVmDFjUPnlzicrVvR7avJEHZtKCeoszeDva+XD
aeapfOqzpdIVmkSNVWV2okY6qcKziZrM0Cw4OPj69eu9e/fu3r07072JD2GF
tm7devPmzY8ePbqbU2Apin7w4MHgqgZRwcP79+/fu3fvjiGBn6yZynQXaBAV
Bm1KSgri88UXX1jPJFVCVF7VqlULZSp3rhiQlRNVQdv5ixcvJkP//EpMpFav
pPK55TjJVKHUPW9fJzx1jF5pzlnNPDNalb3ZFDMTNV6lXielJqpKBaK+yaV6
xhCVnj0FmsGknDhxYs+ePZmxJAazIOpnn30Gw3XkyJHDc2rEiBHt27fPlSvX
kCFDIiIiojj7oMJKmTRp0o8//vjTTz/9mFM/0WLeIMxVq1axxjBDVH9/f/yc
7UpljgZIT0+/dOlStWrV5K7smSJE1Va5cuX+/fdfubPEsKyfqAp6aI8M/fMo
NZU6uD9rrpQRI00GzVF9Zip9+Cnbj5q1O4oq3oke6HeiO1FBVCenQIXiIe31
g4Hw60ePHt2qVSuYqcAjy0YQtWXLljNmzNi9e/f2nMIn4Gq9evU2bNigsbM0
eHju3LlTp06d1quTJ0/CvmUdf7wJCAgAUd+8ecPEAZ8w8wSSkpIyMjL27t1r
JQAhRNWQp6cnqoHc+SFINkFUBT30f/HiRTL0ny1kxfWrVPWqQpx9QwgV1F2Q
ochx7GnOkSnaRlWpotUzUdXDUm+cVAFqoqrH+mEHrly5snjx4vDily1bBtDB
3WaJumTJEjj4iYmJGieb4BNwFReDeNrjU7HCFBMTw/6EJSpsVC5RmXslJycj
UxEZaxj6J0TlKn/+/HBJ0tLS5M4PQbIVokJNmjR5/Pix3BlmNQoMpFq20BqK
4jdW+U8y5eNqhmY4fLOn2LF+lUI9dUqpXs4PGzVWSduo9LDUm1y0jTpWTVTw
c+fOncOGDRs4cODvv/9+7NgxLuiYMal3fGLGp3i/0iPGiNWeP8B6/bBRw8PD
cQGzDwBDVNAjNTUVxuqoUaPy5csnb1UnRGXl6uqKamNDiyhtiKgKeug/NDRU
7jyzAoWFUf1665h6ymuC6h3c5zkLNeeViiyiqrIH+mkbVcH0oyYqM23U92qv
X6m2UXM5wUZ9MDZzrB8W4OLFi2Fp4CHlrgw1Wew21Bo0ZnoY9u3bd+3aNcYS
NkjU+Ph4hqiIZHp6Oj7s0aOHs7OzjPWcEJWRSqVq2bKlbT3ytkVU5PD48eOt
eTaaFIqLpaZO5gzuG3E+lOCXFoSZ+aics6TT2D1SnNRHSsU7KWOV9GRUxuvP
RXv9Y7NnT129evXcuXO6zFFjcfrs2bM7d+7cvn37/v37zDATq7/++qt+/fq/
/fYbOKlJ1IBsor7L6fXDOgVRU1JSMjIyEHjTpk1l3EqFEJVRhQoVUG3kzgbj
ZFtEVdAHHW7YsAEOmtw5J5PSUqnt27S26RPOSR7e6jgLla8rlTVTOTP82SWo
WdP7lazXz86eekd796JYp+/oTtRDhw5Nnjy5a9eu48aNi4iIYEAN0gKVa9as
+fnnn6dNm6ZNVO7IFK+NCqIyVQvPRZkyZeSq5ISokIeHx9q1a+XOA6Nlc0SF
ypcvf/36dblzTibduUVV8cnGqYJlncbsKYFo1e5B1Xkltx81LQdR1adKqftR
6V2n3jnRXj871m+BvadAzhcvXuzYsaNt27ZbtmyBm3+Z1qVLl54+fQoqzpkz
Z8qUKXqIquH1JyQkMERNpcWscFyyZEn+/PllqeGEqMwB9MxwoW3JFokKffXV
V7bVuyKOwsOpbzsJ6z7Vt4+0aWehsrv5qXedYomqVCYrMw+WUs/wd8phoz60
zKkoIOqNGzcGDx68bt06eOuHDx/28/MbNWoUTNN9+/aBqL///vvUqVN5vP6s
+aiMjcrM8NcmalpaGnx//Lxfv365cuWSvnoTojZs2PD169dyZ4ApslGiKpVK
OH2ONe0/MZGaOd2YtVE8J5ka2emqaaCms/NRmZ1SVGqcJqsPP1UfhpI5wz+X
KtJJGcbYqGPFJyrA+OzZs86dO8OGgV0KgxOPnn+WgoKCwNi5c+dOnz6dl6iP
Hz9mZ08xREUtYrx+xuVPo8WYqc+fP69Tp4701dvBiVqiRIkzZ87InXoTZaNE
VdAb/sMgsdotaEQWknnkUNa2/OzcJ17DkneLaaHz/HWdhaq591TmkSgKds0U
s64/WqV85+QUmUsVlsvpGWddv4gCA8+fP//dd9/BLv3tt98ASY09AXDB3r17
d+7cqdFtyxIVLj9LVGbNFNuPyiUqM/n5yJEj3t7eEtdtRyaqu7v7/Pnz5U66
6bJdokI1a9Z88OCB3FkoiR4/purVNcbZN4hZzotn9pQuoioyuLOnVDmIGqve
KUW9ld9bJxVsVDVRLWCjMmy8fv366tWr2eVXAn/F2qjM9ADWRoVZy7VR02kx
RMWbmTNnSrw5lcMSNVeuXN27d7dp39OmiQoh/9++fSt3LlpYUe+0tpYS4LOb
s5ufdpgGdvOjt5tWqU+YinJSvc2VtVOKZYgKo/TatWsgqlFzsbg7pTDLWhkb
VQ9RGajiss6dO0t5gqrDErV27dooILnTbZZsnaho1BYsWIAnQu6MtJiSP1BL
F1OuLuCe8GlOhvpLcxilOoLVvY2/irObnxOIqviQvZufeiEqZze/MZYg6rus
qaTG/SRKTdSnT58yw1IgKrNgircfNSNLTCHcv3+/evXqktVqxyRqkSJFDhw4
IHeizZWtE1VB76Ny4sQJ+1zyj0SdPUOVKJ5zMj//rlBCLVKeEATPnspkqfqE
qTRF1mYpTuoJVPRCVCW9tF89gSrSSfVSfc6URWxU08Tu4c8O9GtMndIYmeIS
Fdq5c6enp6c0VdoBieri4jJ16lQ7eIrtgKgKeq7F8+fP5c5LCyj4FfV5U41+
zhwjSlmkzfkhl5lCBqq0QtBh5Wb2o2pMSVUq2En+7Bapb52Ur5g9/C0wH9U0
sedMMUv+2alTvMNSDFHZ3lQIn48fP16a1akOSNSmTZvaR/edfRAV8vPzw6Mh
d3aKqqQkasJYM3bmN26LPyEXs2ehZkFVlTncr+RsOu2kek8TVX0W6mi1jfqW
Pt9EdkW9yzwL9W1WJyqXqCm0WJyyNirXagoLC/vss88kqMyORtTChQvDzZQ7
ueLIbohaoEABm9iQ1gidOkEVLMjpPtXs1RTGVd6L9cye0mXZKjMUCu7sKWZp
fxpNVObwvgRmLSq9A1WUkypEoXjao0fo+fOvjx9//fTp69evg2kFcfTKAuKG
H5wl3D0kJAQ4xYcMTlmXn13Rzx2W0rZRGR06dEiC7f4ciqgw+8eNGyd3WkWT
3RAV8vX1tdF1Fjx684Zq3szQeL1Is6e0Q9Bcx5o9CZZ7zlSaeid/9jhUVbbj
rzZTVW9VqlceBZ6ULuVfovjDnTsfPHnCnGNy+/btW7du3cjSdVrXrl3D36tX
r+LNVT5duXKF/csV+1uICfDmzZsIH3fBvXDH+/fvP3z48NGjR48fP37x4gVz
HICGgao9vT+DI26x4Nsff/zR0gupHIqo9evXt6f1j/ZEVGjq1KmoBnJnqtlK
TqZm/Uo5qXg3gBL6MmL2lBG/ZQf6s7tSVeq1qB9oqCYw41NKFXM8yluVIkyp
eKNQhO7dGxwRAQPy5cuXwBrTnxlA60mWHtPCG39//8dZ4r7XEPMT9udPaSFA
hIzwcRfcC3eEgYoH9s2bN9xpqFwDVRunugxURgizdu3aFq3GjkNUDw+P/fv3
y51QMWVnRPXy8jp37pzcmWq2Ll7gO+tEYG+qfmNV+1t9OwBoOv6qzBe7bCpz
5ZQya1s/eutpvGJUSpipaqg6qSIUirD9+9+8fcs6/i9pvaD1nBbDWHOEQJgA
mcAZlx93BE7BUua0PhanGkuleF1+bQOV1fbt2wsUKGC5auwgRHVycho6dKid
7SNnZ0SFWrduDc9O7nw1Q+/eUh3b86xj0stMk46OMjqEjBxzqLLM1KwTUT/Q
+/knZO6aop5GFU1vl/pWoYg4dDAsOhqGIvj2mhbTocpYraxYHr7IEvc990Pu
xay4fadMxyljmjJT+t/Sm01xd0dhDFSGqBoGKmOj6ioi/KRPnz6WOzvVQYha
vXp1+5uiY39ERcO3YMECWz3mD+31ssVULid223xerGm750bOnjIUrG6Ms8P9
WounFMlO6mlUSSplgpKZm6qeSaV2/xWKt4cORcbGgmxhtBi0gnivOQrWEoNH
FpIa/+WOOjF/GbE+PmuavqWnSzE4Zf19XT2oBg1URv7+/j4+Phaqw45AVHd3
982bN8udRPFlf0SFUA1sdQPVu7epcmVyctLIQSXN/wrdI0V3gJpLCZjZU9wt
U9LUC/zpQX8nepk/PUQVr15CpYyBpapQvP/333fx8YyhCMSxaGXoygCW+Wus
3mQpLKfgp2izlLVOmVn9vAaq/k5UrlavXm2h9f52T1SY9127drXLpY52SVSo
S5cueI7kzl0jFRND9eyud0TJzLNOhAer80YZ3LNRaJyyQ1Qp7BCVUpWkVIKo
sFTVS1MViuijR6OTklAizKmmLFojciqcFmNb4r9hfGJpzFzP/pYJLZIWEz7L
Um7fKdc65eJUe0zKIFER1Ndff22Jw1PsnqhlypS5d++e3OmziOyVqLlz5163
bp0t7fWH53frJmb9viGTknc3P16LlHXVhViqvGtRFdohZO+VqlKwOGXmprJ7
pwCqWUtTVfEKRdyxozH0oaiMmG33mNP3xJrAz66NYgJn78WcJBVPizlPSj9O
BRqojG7cuFGyZEnRa699ExXP5uzZs+VOnKVkr0SFqlat+uLFC7kzWLCCXlG1
avCt3+e8MeVsKQGmqXawmmehaqI4XXNuqiItc8dUZea4f+ZLlaRSJSgU8ceP
x6emxtGCuRitQwwJWSS+NyRd4cTQYm7HsJRrmmqv4jfBQGU1bdo00aen2jdR
69atC+dC7sRZSnZMVGjy5Mm2MUSVmqrenz97IMl8cpoZgq5FAdkdvOlZk6my
3H8VOz0121KlofpBoUg8eTIhLQ1Yi89SHEcwI2NyKpaW9ocxWorliItQVkyv
Kdc01d4URQOnRrk2r1+/rlGjhrj11o6J6ubmtnXrVrlTZkHZN1GLFSt28+ZN
ufNYgO7dpUp9rHufUo0BfZOpq9ATrJG7V2V3qOaYnsqd9k93q6onACgUH06e
/JCRAazBUGQQx+IuXjyxobF3YUGqwVJenOpaJ2VQa9asyZMnj4j11o6J2q5d
O5veUNqg7JuoUL9+/ay9BBMTqaGDeT16Hf2fnA+zZwVwPzRgrBoO1pCtm8E5
JCWTqFmvtKxJqlnDVYpkhSL5zKkP9BPKVRJHDAMT+cR8yxWDSvZz5g3zCROs
xo2Ss8Tr6Zvs77OCqdyiRQsRK629ErVgwYJnz56VO1mWld0TNV++fEeOHJE7
m/Xq9AnKo4AOomozzQju8X2la/aU0QYqlbNDNSMLp+xaqjT2jUKRcvZMCj0x
Hkxj4PbBwuJSVAOkXJxyN5c2Z3POo0ePiriKyi6JqlQqhw4dakuDxSbJ7okK
tWzZMioqSu6c1qHoaKp9W76J+saSU9/Fhiag6t/NT1/EsixVRSZUnbKXU2XZ
qyoQNe3s2TR1b3FqSk6x0EsWSdzAmdtps1QsZ58r3KVPnz5izaSyS6KWLFny
0aNHcqfJ4nIEoubKlWvt2rXWuD04orRlI+XszNk4Wvg0Jw24iTt7SrPHVU9H
QXaHas4FqnQnAD0HIIuoGlhjWMf0anIByP0vi0RmphP3Mu41usipQVE9LDW/
ety+fVusU1Ptj6h4BqdNmyZ3gqSQIxAV+uSTT6xxo7+wN1SdT7P9/ayTowXP
njJzNz/eYBU8NzIUsRxQVebcRhUvmqjp9Lmi+qFnOWngVETrlKvx48eLcsCf
/RG1Ro0aISEhcidICjkIUaGZM2da1y43aWnU/LmUyrxt9/RQ1KxgdUFYZwgZ
nJ2p2P2pMq1WhSL97DmGqFyxoEvj9Gpyqat9vfaH3M95yakh0U1Trl6+fFm5
cmXz66qdETV//vzWPpYhnhyHqIUKFTpz5ozc+c3Rhf+oIl6GDozOMaxvzFmo
+tmbwyg1P9gMzhttSzUDRP3vvwx1J4dQadBPm4f6DU49wVoOp4z+/vtv8xf7
2xlRv/nmm/j4eLlTI5Ech6hQ9+7dreUsqg9JVL8+HG9aPwP555FyXyadhZrj
v0bNnjIYbA60oi04d06DqBpwE05FjZ/oDyc957x9y4GUVUxMTJs2bcysqPZE
VBio9nZckV45FFELFix4+vRpubOc1vn/qMKeOYnK0ymaweN9C+Qey15dwQoM
gT9YgfjNtFRBVL02qgk4NU3SlO2+ffvMNFPtiaidOnVyHAOVcjCiKmgzVf49
xD58yDJQeUw7veao+bOnjApWcAgKfcGCqOoWhCYqZYzvLxZFJWMpI/PNVLsh
KgzUo0ePyp0OSeVoRC1UqJD8ZuqF/yivwrxrToVNc2IRx2tYmhmsgi8QfbOn
DAeLlP73n8x5Lq3MNFPthqgO1YPKyNGICnXr1k3O3tQPSVTf3pn+Ps9sKD3T
SkWfPcUbLN/sKZ0R0zWtK+eHjkdUmKlt27Y1uYraB1Hd3d2PHTsmdyKklgMS
Vebe1AvnsnpQdeFLIPrEu1jnDi26XypjgnU8okIHDhzImzevaVXUPojaoUMH
a99SwwJyQKJCsp3I8OED1aeXoQEppY5v9f9EoLEqPFjhQ/+GglX3o56XIbdl
FczU1q1bm1Y/7YCoMFAPHz4sdwpkkGMSFWaqPIdQX7rAMVCFv3hZl+NDY/fi
ExyCGME6JFEpM+am2gFR27Vr52g9qIwck6hQ7969k5OTJc3rlBRq4IAM/r5Q
XSNKPMiS9yzUrBB458TqCNYhvX6KNlObN29uQuW0daK6uLjs2bNH7ujLI4cl
auHChaXejPreHapoEb5Z/ToHfXSc+iTIOBQjWMEh6J09RWXNnnJAbdq0KXfu
3MZWTlsnar169awh/rLIYYkKjRkzJl2y3RozMqj/TeRalbwoE2YoGv0yPljT
IqZ7ioJD2qhQeHi4CWem2DRRnZycFi9eLHfcZZMjE7Vs2bLPnz+XKKNfvaQq
VeSd1Z+TSEaNOmnD2fxghXdKCAS+wpGJCs2ePVulUhlVM22aqOXLlw8KCpI7
7rLJkYmKxvSPP/6QKKOXL6Fy5dLaJS/LhBMENwlnT/FvcqWf27qDdWyiBgQE
lCpVyqiaadNEHTdunMSL1KxKjkxUqE6dOpGRkRbP5ah3VKOGhraZEmiFCrYM
hX4ryewpByZqenr6yJEjjaqWtktULy+vu3fvyh1xOeXgRHVxcdm+fbvFc3nv
HipvHmaU39ABJfoAmMHPMe2vTAnWpBB4764VrKPOnmJ19epVDw8P4dXSdona
q1cv2zjP3WJycKJCbdu2tezKjsREqlPHnIeWCrU8jZk9xfm5wuxgs3/Ib7iS
2VNGCWjq0qWL8Dppo0R1c3M7deqU3LGWWYSoBQoUsOyi1Av/UR4e+of4dbFL
x3YoBmxOg0g00hwVEIL+PlsHnj3F6tChQ3ny5BFYJ22UqI0bN46Li5M71jKL
EBUaNGiQpaZRIdiRP6iRonOsx7CZZwjFUgRrTq8CsVEp9Zm30fXr1xdYIW2R
qEqlctmyZXJHWX4RokIlSpR48eKFRfI3OIgqW5rPQOU3IG3xLFTDwRKi0po3
b57ACmmLRC1evLh0cxGtWISokEqlWrlypUXyd+M6yskpk6g8m+blhI8VnYVq
ZMR4X2T2VE49fvy4SJEiQiqkLRK1X79+aWlpckdZfhGiMmrevLn441NJiVS7
tnr7GM2ZOW+QosJDMD5iQnbz46KVEFW9r0NK165dhdRGmyOqi4uL45x2ql+E
qIzy589/+fJlkTP3xjXK4yPjd5rSCcach5aaECy/bWn2Waj8Ecv+0OFnT7Ha
u3evs7Ozwdpoc0StXbv2+/fv5Y6vVYgQldWYMWNEztxfJtFjUjk4xncYn06g
Ge69VPBdqTA7WL0/13WxzmCJjZqlyMjIatWqGayKNkfUmTNnyh1ZaxEhKqvK
lSu/efNGtJyNDKdqVNfR8yl8Pqo2fgVyT99KKLPPQtW1e5WOQAhRs5SRkTFp
0iSDVdG2iOrp6fngwQO5I2stIkRllTt3bjHXT+3dQ7m6CHP5s6/ROnJUkMVo
sWAFh6B/gS0hKkc3btwAMPVXRdsi6jfffCP1VsNWLEJUrjp37ixO3UhJobp3
pbKXnfIabzz2JzkL1e6VmJj45Zdf6q+HNkRUJyenTZs2yR3THIIjkJqa+v79
+5cvXwYEBDx58sTf3//hw4cwpO/fv3/v3j28DwwMDAkJwTV43tPT00Xc2kVE
oiqVSpVKlStXrgIFChQvXrx8+fJVqlSpnqVq1apVrVoVn1SqVMnHx6dUqVLu
7u64Hr8SKwLmq3Dhwsh8EbI14ClVvKjm3n0GjxzVnKTEZ+wZsC11G5BOTuph
sjJlqMqVqCqVqapVqWrVqOp4Vc98Va1CVaxAfVyS8ixIOedWX58jnnojxvuy
2OwpPAJ4EGJiYiIiIoKCgp4+fYpnBAWHZwdP0LNnz168ePHq1avQ0FBcY4VT
elatWqV/fz8bIiqedHn37kP5xsbGovSvXr16+vTpXbt2LV++fN68eRMnTuzX
r1+PHj26dev2/ffff/fdd99++y1MJljUXbp06dmz5/Dhw3HN77///scff+An
+/btu3TpEsJhMGtyfMwhKuCZN2/eMmXK1KlTp1WrVoMGDfr555/HjBkza9as
lStXbt68eefOnXv27Pn777/xdzctfLJjxw4412vXrp0xYwauHzx4MFLauHHj
unXrIihXV1eT42O+gPelS5eKUMxrVlMqFR8w+QBo7lmoWh+qlFSePFT5clTd
utTnTamu31PDhlGjR1G/z6I2rqd27KB27qR27aJ276b27KH+xutv9QufbN1K
rfmLmj+XGj+e+vlnaugQql0bdSAVylH58lG5c5u4naB5RIW9ER0dDU7ikTl0
6NCGDRuWLFkye/bsyZMn+/n5DRw4sHv37nhe8NTgDZ6U3r1741EaMGAAHhlc
s2DBAvxk//79Z86cuXnzJsKJi4uTd7s5YN/Ly0tPPbQhonbt2lW6bduzBOIh
f27dunX48GHAEGBE6bdp06Zp06aw2by9vZGBefLk0d9sAV+4Jn/+/B4eHvhJ
jRo1WrdujXDGjRuH2rVt27YTJ06gthg7qdJYoiIanp6eDRs27NSpE+rz9OnT
169fj3oOvAcHByOZqPyIA54C/fdFKcTHx0dFRcH2hil+8uRJBIKgfvnlFzwR
zZs3r1ixImPEGhU989W2bVtzHX+4/J06CLAn9XzON66kUOib5pTLicqfn6pa
mWrZkhrQn5oyhdqymTp8mDpzmnr8iHoTSkVFUYkJlEGSpKdRSUlUdLT6+pDX
1LWr1OFD6qB+/ZUaPZr69lvK15cq4qWmKye2fBFTmDN7Cs8yjEwwEE3wn3/+
OX78+F69eqFo0HaXLl0argQeBLTmLi4u8Dq1C5Fxl3Lnzo1rChYsiJ/UrFnz
888/79ChA8JBHUODfvToUbiBMEgM1lXRhTt+/fXXeiqhrRAVmS/F1m1ZSkxM
fPz4MRpHVAnAB6UJM6xo0aKoBuY+9hw5OzvDywZ/GjVqhNoyc+ZMmIKg99u3
b4VEUiBR8+XLV7Zs2S+//HLYsGGLFi06fvz43bt3IyMjk5KSRGzuERRojHbh
/PnzaCNg68LSAF2RaZKhFe2FuY4/XH5vLxqAOXjI4Yz2WL+e/k/tLk1l5qQs
vADSEsXVFIU9OXs2tXsndfGi+rwA8VcrJFF4xh88oE6epJYuoUaOoNq2oSqU
V2M8KzK8UwiM2nsKfEPzCv8LXlv//v1hclSuXBn8FDKHU7hgmZQqVapBgwZw
jsaOHQsjB615YGAgACJypunWunXr9FRpWyEqXH7YUZaOBhqgFy9eoIzmzJkD
Fx6NIyx83pbUEkLbXbVq1Y4dO44aNQoN8eXLl2EH6omtfqLCIq1QocI333yD
Zn3jxo1XrlyBSSlZxxRsRRgqiOGKFSvg3KHJ0O8riSVzT8lZtVJQN6MgM1XL
0GVZ6l2EatqEGjaUWr2KuniBeh1MpUg13govL+yN2nzduoWaPo3q8i3lU5Fy
ds45+VaZo/tX795TMTEx169fRwWD+9a5c2c8MoUKFZKgoBX0BI9ixYrB1IE1
snDhQpgKQUFBEtRwAFxPZbYVoqJJsmhehYaGnjp1CiZcnz59UEZwNyxQBYQK
VQW50bp160mTJqHRf/78OW93hy6iIvK+vr4jRozYsmULzFH48pbLN4NCzNEU
njhxAtZ+7969P/30U9jMlss6ZJrpjj9c/o5fcc8G1b0jH49dqm/0nOEVbMK6
dah+fakli6nTp6iQEMOOvEUVF0s9uE9t30b97KcmfGHPbOZz7XM+GxUuCfAF
22Pq1Knt2rWDEyR8vztLCMZww4YNBw8eDKv13Llz4eHhlss22F3t27fXFROb
ICps7M2bN1vo1qgYe/bs+eGHHxo3boxysUyBmyg3N7caNWoA8itXroSRqbGB
oQZRlUpluXLlYJTOnTsXBAsLC7NQjpkmgA5Nwz///DN58mS4hDDILZFjMJBM
d/wDA9TdjLydqAY3JMlmrNaQFl4eH1HNvlDbhIcPUS9fUqlWtlN6RAR15hT1
xwK1yVqhfHa0+YiakJBw8+ZNeL6DBg2qU6eOu7u7JcrRNAEUsFq/+OILPz+/
/fv3wymzUIatXr1a10QXmyBqiRIlRB/lRyMbEBCwdetW+KTVqlWDj2yxchZB
qCdt2rSZMWMGKMoOYHGJCpbC94Hzde/evaSkJHHzSlzBZj59+jTS0qpVK9F9
AdRzWCkmxmzNai14anSlan2icwA9y9jz9KTafEnN+o3675zaJrRmffhAPXxA
bdlC9e2rnovFcjWLqKhXly9fnjNnDiy0UqVKST/yKFzOzs41a9YcPnz4zp07
LbHZIxx/XVtR2QRRu3TpIqLLD5bCjFm/fn3Pnj0rVKhgzRVDQ7DrmjdvPnv2
bNirqN4XL17Eh6jb3bt337Rp07Nnz8TKIgkEexvxR1ratm3r6ekpYi4hQFOO
y0lNpb75WscR0kaO9TMg8ipMfdWOmj+PunJF/MEmi+rFc/VcrF69qLJl1Am5
cOFDcvKNGzcWLFjw5ZdfytshZpRgJlWpUqV///4wnMBAEXMIFeyrr77ivalN
EHXNmjVi3Qi+MLK3a9euZcqUsVhJWlYeHh6wV+Hab9mypVOnTmganjx5Ilb+
SKzExMSrV68iLU2aNBFrHoWXl5cpZknwK6pYUX6XP7un1NBAFcPSPK5Us8+p
BQuoG9cp6/YX9CkwgNq4Ie3bzs/27l2waBHsUmvrExMomEwVK1aEB7d7924R
D89dsmQJ7+2sn6hoEx8/fmz+LWDUnT171s/Pz8fHx5IFKIWcnJxat26NMh03
btzr16/Nzxx5Ba6eOnVq5MiR5cuXFyVzTJlot28PlSsX5zQ9HpffwOwpBqeV
fNQDPefOUhLO57GQULXWTZxwZNu2rt27582b1/yikVFKpbJatWp4XuAZibJa
+c6dO7xjAdZP1EaNGuGJMzP8gICAxYsXf/755/Ku6xFFxYoV69ev3yFaaHyH
Dx9+8uRJ87NIdoWGhm7atKljx44GN6MwqEGDBhk91XbkcGO3RskxboVXoYJU
p07Uti2UlY0JmiBUJ1SqYcOHl61Q4fiJExfOnx87dqwdmCJoF1q2bLly5Urz
O1fj4+Pr1KmjfQvrJ+rkyZPNCTkmJmbfvn09e/YsWrSohYvL4oL11bhxYzQN
zKEwFy5cUNBTrfDhn3/+aanjliRUenr6rVu3pk+fjrpqzqYBVapUMW4T3ZgY
qlYNAWee6vD08bdBPfXw0907Mk+IEkOoSKhOqFSoWsjM8/SaqYiIiK1bt371
1Vdubm6iVWiZVLJkyf79+8MgMfP0z9GjR2sHbuVEhUlpzvHBIM+vv/5ao0YN
y5eSxVW4cOG+ffvCO2Z9Fu5Yv7e398CBA8+cOSP9ujzRFRsbe/DgwU6dOpk8
xRE/PG/U2smrl6l8btoeveEj9oBT/LBLZ+rfI1S8zR/Oi8qDKoSKhOrEZuZ/
nNlTN27cgLFqu2MQrFQqVd26defOnWvOJKLDhw9rrwizcqKWK1dO4JJMDcHp
u3r1KuqGDQ1N6lG1atVmz56tcV6hxnxUWBRNmzaF42wfZxzcuXNn5MiRJnsW
xu1MPn9ujr1BBM6ewqt4cfU2Jg/uWSwbpBOqDSoPqhBjmrL6L+d8VBirq1ev
btSokQ1NktElLy+vESNG3Lx507QcCw0N1aaWlRMV3roJoSUlJe3fv79Nmzbi
rimWRfD0mzVrtmvXLm0PhXfNVIUKFeA129ZMKl0KCQlZuHBh9erVTci3Fi1a
CF3rDZu/XRvBu6NwcFqrJrVkkXpRp+0LFQbVBpVHOyf/01ozlZKScvz48c6d
O8u7TkoUwQvu2LEjrE0ThqtgtiETNAK0ZqKiEVy3bp2xQYWHhy9btqxmzZpS
lYkF5ebm1q1bN1Rp3nEWXatQPTw8BgwYAAdNjJKRWQkJCbt3727evLmxSzAK
Fy4sdAriqxdUsWJao/w8C6Cyl5Q656ZataT277XhyVEcoaqgwqDa8OakNlEZ
3bt3D06EffiA9erVg+FtAgmXLl2q0eFvzUQtUKDAw4cPjQoHD9G4ceNKliwp
YWlYSqirfn5+jx490pVYPTulwDhv3779yZMn5d1MUhQhCefPn4e3YtQEHtRz
oFjQDQ7uV28DxdODqmmyZrAdpwP6qXc4sX0hb1FJUFX0eHO6iAoFBwfPmDFD
+Lnw1qwyZcpMnjzZ2OHdmzdvauxTYc1E/eSTT4xaUPn06dPBgwdbdCMOyeTt
7T1lypTQ0FA96TW4m5+vr++BAwfsYKwKevz4MQrXqIFmtEeCgp4wTui8KVzm
7k6NGK6e/W77QsVA9UAl0Z+NeohK0b2vS5YsqVixovBysVrBhBs+fLhRPWZx
cXGVKlXiBmLNRB00aJDwEPz9/fv162cH000hZMXcuXMNlouQ/VFr1669fft2
+zicCw4IKrzwrTnACsNdqciZ5l8IIiquKZCf8vuRevlCitRaWKgSqBioHgaz
UT9RKXry6oYNG4ScvGz9gh+Ehhu2mfCchPfEDcFqiapSqdavXy/w5w8fPuzV
q5e420HLJXgfixcvjomJMZhqgTtOo6pv3rxZyi15LSc4ZT/99JNAqHp6emrM
juBR8CuqqDfflss5Z0+pcVqAGjOaCnolSUItK1QGVAmBDDRIVIoeqwKf4VQK
CdDKBatswIABwtdprlixgtuVarVERWNx756gSSl3797t3r27xpQPG1XJkiWX
LVsmcOKx8FNRKleujCfIPizV4ODgUaNGwUEzmGrU83379hkI7shhyknFOd5O
x0Qpj4+o8WPVR43YvlANUBlQJQRWHiFEpehT2Hbu3Gkflipss759+wocxLl2
7RrXNbZaolapUiU+Pt7gD+/cudOlSxf7wGnRokUXLlwoJNWMjDpnCvm5Y8cO
++hTDQkJGTdunJAdVnGZgbAm/8/AIX3470cfUZMmqs97sn2hAqAaoDIIrzkC
iUrRUN26datGv6KNClCFOy8EqtHR0dz9KKyWqD169DB4Tt/Lly+7detm5Vub
ChQK4rfffouNNWILTWNP7oNTdujQIfMKylr05s2bYcOGGSz6pk2b6tvZD+1L
qxYaW9bnmD2Fr1ycqR9HUJbcE15KoQIY65sLJypFu//r168vUaKEUbewTsFO
6927t8GdiIAp7qxU6yQq/LUlS5bo/8nbt2/9/Pzso+80b968o0ePNrYgTDhd
un79+hcvXjSjoKxIAQEBHTp00L/8v0iRIvqeiLBQ9dl5uub2M59/25l6bg/L
JSAUPSqAsXXGKKJS9EDVnDlzdM1utS3BnZ8wYYLBRYhz585lf2KdRHVycrp2
7Zr+6+fNmyekM836hcT27dvXhE35TCAq1KZNGz1zXG1LqCSfffaZ/rw9deqU
zt9f+I9yzsV3DGjWqqjGvtRNe1goAaHQUfQmVBhjiQoBKWPHjrWPiTeenp6L
Fy/Wv4f52bNn2TW51klUb29vPWdvwczeuXOnfUzjh5o1a2bsQgZGphEVkOnX
rx+8ZjOKy4p08OBB/buq6jsddeVynfOm8HllH+rovxImxYJCcaPQTTvV1wSi
UvQAYrdu3czZQMx6VKZMmX379ulZLANziD2HwjqJ+sUXX+gZmIbVYeZ2Uijo
3Llz58mTJ1++fO5ZcnNzg/ctcTdC1apVTd5cyzSiKujFrdOnT0+Q8KgONIJo
5VHKcAnj4+Pj4uJwd/w3NTXVzFVdCGHlypXcvZI0BJLo/PGwIewof4bGjlLF
ilLr1lLmncWDpCF6SCYSiyQj4Ug+/ousMDhGIKJwdxS3ybvwmUZUih411u9B
iCtYiXii8QhzH2q8Zx5qM8+Ir1OnzoULOlfJJSUlsSm1TqIOGzZM15VPnjwB
b03IbQ8PD9yiadOmnTp16t27948//vi///3v119//f3332fPnj1r1qwZM2ZM
njwZ3krPnj3bt2/fuHHj0qVLFypUyHLtbMGCBdeuXWsyUkwmqoKeV7Bjxw5T
i8uw0CBGREQ8fvz4/PnzaN/XrVu3ZMmSBQsWIJ+nTp06ceJEPOPz5s1bsWLF
xo0b4XGcPHnS39//7du3JkzxAqlQcLrWUX766af8c3Fxo4YNeA6WwieuLupz
SxONbnEQeSQBCUFykCgkDQlEMpFYJBkJR/KRCTCbkSHIFmQOsggZZdGJbSho
czYHNpmoFD0QZrk1qnio8XjCQ/n888/xwKLpZDIZDzXyGQ81Hm28/+WXX0aN
GjVo0KDOnTvDH4TBiefOhOHsNm3a6FlOhbszl1knUcEZ3svQ2oKEwpsbtE0V
KlTo2LHjgAED5syZg2BhEN69exc5ExYWFhMTg8YlhRaqNN7DkEBuBAYG3rhx
Aw/Fhg0bUP+RVy1btkRBiHswBFKBtJiz5605RFXQqIEVYfLdeRUVFfXw4cN/
/vnnzz//ROrg9zVv3rxmzZpom2BGov4XKFAAhgToB5MJ/y1WrFjZsmWrVKmC
9qtr166o+fghWHT9+nUEJfy+cLu+/PJL3mTiLvyLtYOD+M+SxidftTNqrhSi
iggj2og8koCEIDlIFJKGBCICSCySjIQj+fgvsgIZgmxB5iCLkFH4ITINWWdU
qoUIRYyCNqeemENUPFnAmrhbVMHsLFeuHPgGSC5cuHDLli1nz569efPmy5cv
o6Oj0bziQcbjzDzXAAseMTRzQUFB9+7dO3fuHJo5tHFDhw6FZeXj4yM8boDw
uHHjdB2WwR47ZYVERcx17Zu0a9cuVEiDaUfjVapUqdatW48ePRoZfuvWLeSn
aYuG4LWhpC5evAi6ogVEOYo1M6RRo0Zm7rlnJlFhe8NWF+URRh1+9OgRbKFJ
kyZ16dIFj3CRIkVM2D8zd+7c+GHlypXbtWs3YcIEBHj//n2BjQ5aQN6udVSn
Y8eO8fzgzGn1FlIaG0wBp6U+ps6eEXJHRAzRQyQRVUQY0UbkTZgajYzCD5Fp
yDpkIAJEZopyRDgKF0VsppNlDlEpei84sMucCDBCKoAI2KKwOTdt2nTlypXg
4GDTjkgGadEEo63Zvn37+PHj27ZtC3tJiJ2GYkLDxxsm3A0mBCskKprvML6T
egICAho0aKA/ybAEUDOHDBmyZs2aS5cumbZbtS6hfl69enXVqlWwWj/55BNz
lhWgaA4cOGBmfMwkqoJu7pEcc3oykScw+9Hof/fdd5UqVRLRjEdQYBQ8tRkz
ZsB51DNSyQiPybRp03h9fzgaPD9YuohnMr+zMzVrJmVoHQQigyghYogeIilu
qpGNyExkKTLWnPYOxYrCNX/jIDOJCuFJNOdMRpRprVq1Bg4ciIcathYMUTPj
wxVy+Nq1a+vXrx8xYkT9+vUNDqM0adKE1+UBopnOfCskatOmTbWbHhjbP/30
kx6zBw0EKDdy5MiDBw+GhoZabhc7xA1W699///3DDz/AcTOhQwZRHTNmjPkL
7c0nqoIeGjPN90fFPn78OGwqlJcQx8Fkubu716lTB970kSNH9BMGtbpVq1ba
IfTq1Yvn6sEDmWGpDO7pe+3aUnr3+0IEEA1EBlESvmeLCUKWImORvchk0xiC
YkXhmh8T84manp6ORs2EyVR4uGAg+fn5wfyARWrR4TxYcSjZn3/+GfTW81Dj
K5i12g9vcnIyMzhlhURFY6F9wcKFC3X1eACzDRs2XLZsGXwlM4/iMkq4l7+/
/8qVK3mPRNSjr776ShRfWxSiKujpW0bVATik27ZtQyrgZUu2/hfNUPHixdu0
aQNzQk/uPXnyRHsVJM+2kMkfqE9rZ9moWUStXo0K1LnpEG6KWyMCiIaZA8fC
hexFJsPVRYYb1Q+AAkWxihIH84lK0aOHgwcPNuq+ABSMUhSo8HXZ5ishIeHx
48d4qGGL6iplNze3FStWaP+2f//+Cqsk6qZNmzS+vXfvXunSpXlTV7hw4enT
p9+/f1/IZk2WUGxsLDwRNG0C7TRcdvbsWVFuLRZRYTz8+eefAm9669atYcOG
lS1bVpYTZ3DTUqVKwdfWNW8fZgweQw0bo0iRIpoHtIWGcFZLKTK35d+4kdJh
BeF2uCluLVeqkeHIdmS+wGJCgYo1wV4UokIPHjwQeOQfHuqxY8fevn1bSgOJ
KzzUiO2sWbN0zZGoWLGi9uZUMOoUVklUjXEEPCPDhw/n7V2vV6/enj17IiMj
5Yo2o4yMjJCQEMREyBK/n376SayN9cQiKlNDDJ4hgmj/9ddfdevWFbJFiUUF
VlSrVm3p0qW81guMSRgY3Oth6V26dCnHRTeuUXlcc5zW17wZFc2z2BC3wI1w
O9lXACHbkfkoAoP1B0Up4hbQYhE1LS1t9uzZBscrfX199+3bp3+vdWn09u3b
/fv3w//VjiRSMWrUKI2uxUOHDimsj6gw4WDnc7+CBejl5aWRIhjkvXr1unnz
pq7JDNILThni07t3bz0uIdLo7+8v1h1FJCriPG7cOP2rQkaPHo34W88JmCVK
lPjhhx94d0DdtWuXhjG5devWnFfszDFdytVFfWiUlhA4bmE9+34g81EEKAg9
a5ZRiChKEfslxCIqRS/d0nMAHIqsX79+d+/etZ69fBETmMpw57V7t4oXL66x
3Shini9fPjR8VkXUKlWqcPuL0K6xU2dZeXt7o7F78eKFtR2ihPggVlOnTtVl
xc2YMcO0+R68EpGoCnrOv64hKjibHTt2tMK9LwoUKNC6devjx49rRBhem8YQ
1eTJk3Nc8duMHAZqu7ZUnOauXwgWgVvh3hEoCBSHrh4AFKI58/m1JSJR8YCs
W7eOl/ZIFLzsly9fWuFDjVjNnz8fCOVGGF7zsGHDuINl0dHRZcuWdXNzsyqi
NmrUiPv5xYsXNQ5bxGXbt28Xd1qUuIqIiFi+fLn2usgyZcq8eiXmDvDiEhU1
ZPjw4drDqWfOnGncuLHV7vEF46Fq1aqoEhrR/ueff7hDmd9++22Or3t2zyQq
/rrlpf49rPFzBIhgrXbfXRQHCgVFoxFtPV1kJktEolL0kJn2SG6xYsX++usv
a36oo6Ki9u7dq9EPXKRIEe7MebC3bt26qHVWRVTuaWupqandu3fXyPlt27YZ
XJCOH8ItukcLpvgdWoGBgTExMdK0gGitEE+NRg22q7jTP8QlKlNDHjx4wL3F
oUOHTJshZqzy5s2LCgAPBXWyZcuWn3/+ua+vb7169XD3ihUrGjQUK1SooHHy
aVxcXLt27dgLEGy278Ndf4q/X3ekcvbHIijek+u5ghuCiCF6iCSiiggj2rgL
koCEiLu8jlcoFNxdY8NbFB8KUdwbiUtUCPDkMh/ZtXPnTrlGloUrMTFxz549
GpuODhw4kOt19u/f39XV1aqIunLlSvZDNMHcR8nLy2vjxo26plLAMjx9+vT6
9etHjx49YMCAFi1a1Myphg0bfvfdd0OGDBk3bty+ffvu379v0e4axHPHjh2s
pVqiRImAAJEP0BSdqKgh3E3vjx07BjvNch2nMLRq1KgB63Hu3LlbtmxBcd+8
eRMt4KNHjx4+fIgCQoN4+/btq1evMgs8J0yYAF++cOHCvKH5+Pjs37+fmz9H
jx5lzdSSJUtmLxt5F0mVL5c5ATWfG3XiBPdXCARB8d4Ct0YEEA1mqSwihugh
kogqIoxoI/JIAhKC5CBRSBoSaDnzHkWDAuKO5KL4RN+GQnSi4lGtXr06E3jR
okV37dol5aY95gjxxEPNtZQKFSp0+fJl9gIUOvwaqyIqO4IAc47bg8psKqI9
mwJpvHDhwm+//da2bVuYB6VKlfLw8MiXL5+2WcVsTePu7o6gYIHA9ejatevS
pUvxLFjIcEXcNmzY8NFHH+HuI0eOFLEHlZHoRIWQgcySEAQOGlhol5iyZcui
1QN2wB/4DqiByCtd+YPSgXkJsx9I9Pf3h1U2ceJEtI8a85MR1cqVK3NtNoTJ
zsmE0Zg9JhgYQHnkzyRq61bcHVHwcwSikWrcCLfDTfEtAkE0EBlESVe1QUJw
a2aDCCQQyURikWRL5CSiimJioIeCQ/GJfgvRiYp8mzdvnoJ+qJE5toJTRrCU
Nm/ezG3Wuds6rVu3znqICisOGGTnar58+ZI18IDBJUuWaPgFaOnWrFkDs7Na
tWomrKdGVcSTgpvWr19/1KhRwLLoxKNo33P27NlIiMBTCI2SJYiKdge1Ha0M
ssUS1imMk19//fX8+fOvXr0y7VFKTk4G05gF9d27d+euskSZInzuVNVVq1Yx
eMTf7GnA5/+jVPRpffi7PntPHvwQP+fiFIHjFsz2AripaTtEIZlILJKMhLO2
mYhCMaGwUGQoOEsUmehEhZ49e1a+fHlYdHLNODVHiPNff/3FWEoK2ggJCQlh
vjpy5AjcamvoEAZRYUujzWKnhSxbtoypHqjhkydP5h5MgIp94MCBjh07wqw1
f5YgwodZCyzDjLxy5Yq46YqKioJTAPMGxjDQOnXq1OnTp8+cOfOPP/5A63z6
9Gk0HCa30SYTFa0Pcht2F2wnPz+/X375ZdasWaje+Dt69OjVq1ejFYbloz1p
zRzBSEPyb9y4ERkZKUp/MqxEPJibNm1q0qQJi0G8qVu3LtvBEhQUxPpo2StH
dm7PNFBLfUxlPQv4CX7IDQfB4ie4hSibliDJSDiSj0wQ115FMaGwUGQoOBQf
W5QoVhQuihgFjUwweZTNEkRNTU3dt2+f7DPJTRasuxkzZjCAcnJygmnKfA4X
BoC1hnSBqEWLFi1WrBgzvxR1uHHjxkyBNm/enDvd9/bt20Af3HbRu6fQuNSs
WXP+/PnmG+14kFFhJkyY8PXXXyMhsE8GDRoES7UwLTwCSGmZMmWqVKnSqFGj
Xr16zZkzB0aysZ3zxhIVRQ+XdsiQIStWrDh37hzsLthOaF7Dw8PRqiLV+Ius
xn/x4a1bt44dO8Z0Bpo5IdPZ2blLly6wAOFWiN7BAi/swYMHaKfYcVh4Ov37
92c6yeF3MGsDFfTUtczfLJibSdShQ5hFUrgYl7E9RQgKASJY0dc/IvnIBGQF
MsTM5VcoFKYLGsWEwmLKEcXHFiVTjihiFDSKG4U+ePBgVABjp6pagqgUPdBj
iWAlE3wWdgPJVq1aMf4Lsh0PtcFdfSQQqjSAA04yxx8DQcyW48AsW6CI8+LF
i2FIWHSKIO74/fffX79+3YRU4Hm5du3alClTmjVrhrQUKlQI2EeE8WDC+uXt
44IthJQi7TCSv/vuOzR2wg+cEk7UPHnytGzZErmHdIH2sbGxQqxElAWeTRhv
J0+e/N///meax4rmA+1FYGCgRQ+2ZsYl2V3jUEPYLXYReYZdsNYyr/5hqBqn
eVypc2eYD3AxW6kQCIJCgJaLLbICGYJs0TXKpl8oCBQH0oWiQQEJyVgUNwod
RY8KgGqAyiB8X1ALEdUOdPHiRWYDSXd396tXr1K0KYjnnXfrPIkFoqJ2sZMG
R4wYoaCNjQULFjDwh2sM3x/OC9cvQzONZgLmH8yPZcuWrV+/fsOGDWvWrFmy
ZAk86+7du8PfYbs7hAuVDdmydy/PIho9unPnztixY+F/eXp6csfF4H9R9F5z
y5cv128e4L6gLmo7kiDEThZIVHivf/31F/wRk7dBwzOLZhcPIzzWcuXKCc9J
PPu7du2SpqMekXz69Gnfvn2ZW8MYY/quQRKUJj5p27ZtOmMhd2ivJmrDz5hJ
U7gMFzO/ws+fPHliUfizQrYgc4w66xmZj/YaBYHiMDmSqAaoDKgSGmt1dYkQ
VZfwUC9atIhpr5lJMrCpgB1rWEILosKimzhxIt4jPsxj27FjR6aPF3UAsGLP
xkK7AEMCsIUt8fjxY/g1kZGRcJlhCjIH+uB6fPLs2TP4O0eOHAHTvvjiC6M2
ilSpVOXLlweihXipUVFRCxcu/PTTTzUWIyjoWYvs2hZchofa4K1B448//hhe
IQx1/fc1SFTY22AgvFdR+v8ZjxX+Y48ePYR4rA0aNDh79qzEzt3Lly+HDRum
ooU8ZBIOa1BBHxWU+OEDlZpCNaIno/6h3jQVF+Ay5nr8ED+XMrbIHGSRwV1/
FXTPCbIdF4vVc4KEo2KAzwYXWBGi6hGaRdQfBd2CM34Nnrjg4GC546UmqoeH
x+zZsyl6vAxUgTl68+ZNil4LPGTIEAZWQA3qAIoY/s779++FjM6jHQGWHz58
uHPnTo2hYYOCxQjTV3/4t2/f7tq1a7FixXgnGsFI5o5r4InQpi6vYK9Wq1YN
oNZDJP1E9fX1PXjwoOjeK/L8+fPnf/75p8b6BQ199tln8IOkMfY0BN8W7W/u
3LlR1vBW8AmMOldX19KlS0fBSk+Ipyr5qNdJ3bmNr+AC4zJcjJ9o7k8liZBF
yCj9UEVWI8OR7aJPR0H1QCVBVdFzd0JU/YJzCi6hCjGTTFDlxF0aaZoYos6b
Nw/vR40apaD3aEJlCwkJ6dmzJyw9EKZbt27Hjh1DHTBtpJgZGt62bRvvpsS6
VKJECe3dBVkdOnQIz4KeBTLTp0/XSObw4cOF3x2gRj7o6pbRQ1TkFWxjyy1h
QHN24MABXT2r8GQvXbpkidloAoVWGKYC2mW0SqgwsMfwBuQMCQ+n3kZShTyo
mp9QiQnhERH4HJfhYhmP20ZGIbt0uf/IZGQ1d66LuEIlQVXRWJzIFSGqfqH4
0Bwjo3755ReK7pO3EqJ6e3uDXTAp69evD7reu3cPRB05cqSbmxsc6pUrV4KH
+NbMG8Hk8/f3nzhxovD+1XLlyh09elQ7qB07dugfOXVxcdH23JEuPUchawtZ
gTaFnfDGlS6iDhw4EHll6fW2aKHOnDlTr149jbvDi0RDI4t1ylV4eDjyDbRc
vXo1/os8gRPhHxhIPX9OOamoH9Szsv9avRoX4DLZB2fxVCLTtB1wZC8yWZTp
W3qEqoIKM2jQIN7qRIhqUHCBCxUq1KRJE5Tj3r17eZ9WiQWili1b9vLlyy9e
vIDJ169fP8Bz+/bt8JE7dOgA91/cZb+w+tavX69rF2tt1a1b9+nTHLu77969
2+CsQrWbqbXbPNKFZkLgfRnBuOrRo4e2/85L1L59+0rWRCItiAN3fzY0IkuX
LrU0AQQK9dzHx6d27drM4kFE78LVq9StG+od/P7eHR2fgK9wAS6TO6ZqIdOQ
ddw5gchYZK/5VoRAodqw43pcEaIaFOyHwYMHu7u7BwUF3b592xrWTMF0rFKl
SnBwMMxUOPhXr14FWitVqtSyZctHjx5ZwtyCJ/jPP//oWsGtIVgyvXr1Yrs0
T506JWRH32+//ZY35jdu3DB2ZzwY6j/88IPGAJM2Udu1a8d/krLFhLoEA56d
sIpcEv18ZJMFg4GpTmj+UNXROu/65x/q+DGqsCcVGrpt1258tXnzZhl7JzSE
rIPBzOQkshQZK7Gpj8rD3V6GESGqEAFZsHxQ0+DvWMNUW8ShRo0aTI2CUYr2
Gm8aN258584dy3mvuAsqrcAFLPnz54dZS9GLa4Ts1Q/NnTuX977JycmArZAQ
uAKENQLUICqaJOGnZogo+BfIGRhX5cqVsxJ7j1VsbCzsLlSk+Ph4eNCLV6+m
tm6kmvrGJ8TjQ3yFC+SOYw4hA5GNyExkqSwbL6MKoSJx6xUhqhChsDp16tS/
f3/4FLJ3eVE0UWvVqgVY4e+JEyc2bNjg6+sL7Fv09EOKzoddu3YJHH+HzXz/
/n2md87gxbjmwoULuu77999/m7BFXsmSJU+ePMkGwiUqPA60j3KZWzExMcOH
D1+4cKH12Husnjx5UrduXTSdEydOnPDrTOqP+dS0Xw4cO4oPNU6LsAYhA5GN
w4YNk2t3O0QAFYl7zCshqkAdO3asYcOGVrItIYjaoEGDS5cuwXJ48ODB119/
Dc9amsczISFh1qxZugaYihYt2qxZszFjxixYsGDRokV3795dvXo1s60cd6dE
bXl5eelZOvH27Vs9O3C60OL9CpFh92HgEnXIkCFSHhmpLbjV1rCcWVtolFFk
I0eOXLdu3fBx46gp/6M2b+w/YgQ+tHR7bZqQjfIOFqMioToRohor5NsXX3wh
+qadpglY69q165YtW8aPH79mzZrFixdL1iFP0bPytLuPfHx8YNXAtoEjFhoa
GhUV9f79e8QTf9+8eePv73/69Onp06frmkHUtGlTPUnIyMhg1oWxqlixInIA
3MaDv40W3sybN+/777/n9tm6urrChmECYYlaunRpEY+vsj+haevRoweckZ8n
TaKm/BJ5YG+XHj2sYamg1QrViR23JUQVLphevPOCpBdINXXq1BkzZsBywBvp
px/AQ2ePh86TJ8/gwYMvX76Mh04PFVNTU2FOXL9+fdSoUdpzsXr37q3/jgcP
HmSu/OSTT2AkX7x48dmzZ+A2WrpEWniD/wYGBuIr5Azbu1WpUiVm7T9LVHGP
r7I/wRZFFm3atGniL5Op6VPPb9kybcYM6zRQrUSoTsgxQlRjtWPHjhUrVsgd
C7UAkLVr18Lkw1/ESvrTuz58+PDjjz8q6H3aly5dCrdL4BPHHC2Np1XjDBpm
/ZcegYoff/wx0H3t2jU48npux2wEB8IPGjQoF61FixZRWURFIBKP79uiLl26
NGfuXPWCi7mzV82be0HjsGkiLaFSMf1ahKjC9fTp0zlz5sgdC7WSkpJ27tw5
f/789evXy+WO3b59G3YgfG0TdhSBPXngwAHu7lIaBwBpCwzfu3dvUFCQwOYD
XAXnwQQ4/jVr1sQdYVfjRsOHDycGqkHFxcUtXrx41eLFMetWr1iy2BY3OpZY
qFTM+j5CVOGCr71y5UrTdiYXV3CuQSTU+StXrsjljgFxx48fN3k6DRqF7du3
s5vCGZzIBJCaMG8tIiJi2rRpzs7Op0+fvnr1KuzVc+fOmRZhR9OJU6c2LV3y
//buYCWBKArAcC/jyp2PIq5ciltXPoIg7mqRLYLa2CLBheAuCYyIpCBNQiim
dBGVzSIFK8OUTuOmIkQnZ+699n8vMIfxzpwzzplzL7c2974M+ccUsrRYYHOR
i7pUKunQ4T8cDiuVijzvq+0P/GNykboxmUyuOF85WZa1qKh+6HQ6kUgkkUhI
8RAMBnXrqNTWo21vr60ebazfPerYk6AhWVqywPZJQPNoNps6XJJyby+Xy5Op
rUZrtVqBQODX708XqFarhcPhQqEQj8f9/8/ZUJ87cezsnOR3Bxo0YBtBllYs
FpMHN9WBmKTb7frZpzRFsVjUsON6XqPRKJVKhUIhT8+q3Byy2Ww6nc7n894d
ZcmMxuPjg8rV4cGQHDSzXC5X/r77NqaTC1+TIkdSoZIBlQvXaDSi0ajXR5Hs
k8lkJiNkMaOzatU6PaFranZVh+oo4Ib8cMqHqi3EYDCYdDd5SlKhVPU67L9g
kIt6/ea8rjoKk9w6VEcBN7zYelIVKR19qPylGHa9ddT/1Las++tr1VGYpNfr
6fCeBS60220lw3a8YNu2D3dUKek1mURqis7Dw9NSPAf55tWhOgq4IeXW0nSq
+5MaZKkvzRnzx0u///b8rDoKk7w7VEcBN/jOel6avFI0yNihOgoAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAcOMD6qadLw==
"], {{0, 319}, {454, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->{367.1343749999999, Automatic},
ImageSizeRaw->{454, 319},
PlotRange->{{0, 454}, {0, 319}}]\)](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/498a7fb0bf8b594f.png)

![polygonCircleSketch[f_] := Graphics[{Black, ResourceFunction["ModularTessellation"][f, "ApproximationPolygons"],
Red, ResourceFunction["ModularTessellation"][f, "BoundingCircles"][[2]]},
PlotLabel -> f]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/2dfa50e93dcb7e21.png)
![Graphics[{MapIndexed[{{Yellow, Purple}[[Mod[#2[[1]], 2] + 1]], #1} &, ResourceFunction["ModularTessellation"][6 ]], Blue, Values[ResourceFunction["ModularTessellation"][6, "BoundingCircles"]]},
PlotRange -> {{0, 2}, {0, 3/2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7468d24208f5472c.png)


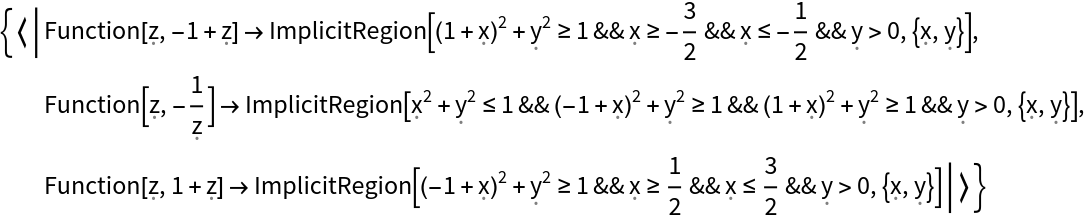
![]() :
:
![Graphics[{RandomColor[], #} & /@ Flatten[ResourceFunction["ModularTessellation"][{6, 12}, "IncludeVerticalStripes" -> False]],
Frame -> True, PlotRange -> {{-1, 1}, {0, 0.16}},
PlotRangeClipping -> True, AspectRatio -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7590a0db4dd04b8c.png)
![]() are included:
are included:

![]() :
:
![Table[Graphics[{Gray, ResourceFunction["ModularTessellation"][2, "ApproximationPolygons",
"IncludeVerticalStripes" -> False, "PlotPoints" -> pp][[3, 3]]}, PlotLabel -> pp],
{pp, {2, 6, 20}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7323e5f0bb5b8095.png)
![]() have infinite area):
have infinite area):
![]() :
:
![{evals, evecs} = NDEigensystem[{-(1/y^2) Laplacian[u[x, y],{x, y}], DirichletCondition[u[x, y] == 0, True]}, u[x, y], {x, y} \[Element] fr2, 100, Method -> {"PDEDiscretization" -> {"FiniteElement", {"MeshOptions" -> {MaxCellMeasure -> 0.001}}}, "Eigensystem" -> {"Arnoldi", "MaxIterations" -> 10000}}];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/28e9f70168869700.png)
![Table[Plot3D[Evaluate[Abs[evecs[[j]]]], {x, y} \[Element] fr2,
Mesh -> False, PlotPoints -> 60, Axes -> False],
{j, 6}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/655a389ecbc1ebef.png)
![rescale[Polygon[l_]] := Module[{xs, ys, minx, maxx, \[Delta]x, miny},
{xs, ys} = Transpose[l];
{minx, maxx} = MinMax[xs];
\[Delta]x = maxx - minx;
miny = Min[ys];
Polygon[((# - {minx, miny}))/\[Delta]x & /@ l]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/2339240e525df47e.png)
![Graphics[{RandomColor[], Opacity[0.8], Thickness[0.01], Line @@ rescale[#]} & /@ Flatten[Values[
ResourceFunction["ModularTessellation"][{6}, "ApproximationPolygons",
"IncludeVerticalStripes" -> False]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/44412c9294642c66.png)

![polys = Flatten[
Values[ResourceFunction["ModularTessellation"][{16}, "ApproximationPolygons",
"IncludeVerticalStripes" -> False]]];
Length[polys]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/70519c37abd8f262.png)

![Histogram[
Last /@ Cases[
Values[ResourceFunction["ModularTessellation"][18, "BoundingCircles"]], _Circle, \[Infinity]],
{"Log", 50}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/25572a58566a7929.png)
![radiiSum = Total[Piecewise /@ ( {{#2, #1[[1]] - #2 <= x <= #1[[1]] + #2}} & @@@ Cases[Values[
ResourceFunction["ModularTessellation"][16, "BoundingCircles"]], _Circle, \[Infinity]])];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/1a069f8efa3332b6.png)
![radiiSum2 = Total[Piecewise /@ ( {{Sqrt[#2^2 - (x - #1[[1]])^2], #1[[1]] - #2 <=
x <= #1[[1]] + #2}} & @@@ Cases[Values[
ResourceFunction["ModularTessellation"][{10}, "BoundingCircles"]], _Circle, \[Infinity]])];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/60dbacf874711c45.png)
![polys = Flatten[
Values[ResourceFunction["ModularTessellation"][{16}, "ApproximationPolygons",
"IncludeVerticalStripes" -> False]]];
Length[polys]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/57c22ae004287e8b.png)
![perimeterAreaRatios = (Perimeter[#]/Area[#]) & /@ Flatten[
Values[ResourceFunction["ModularTessellation"][{14}, "ApproximationPolygons",
"IncludeVerticalStripes" -> False]]];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/79fb82b65540a938.png)
![rt[z_Complex] = RegionMember[
ResourceFunction["ModularTessellation"][
Function[\[FormalZ], -(1/\[FormalZ])], "ApproximationPolygons"], ReIm[z]];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/032b8079d9831e47.png)
![ComplexPlot[KleinInvariantJ[z], {z, -1/2 + 10^-4 I, 1/2 + I},
Exclusions -> None, WorkingPrecision -> 25, Method -> {"RasterSize" -> 400},
ColorFunction -> "CyclicLogAbsArg", PlotPoints -> 120, MaxRecursion -> 2,
RegionFunction -> Function[{z}, rt[z]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7ef24d441d498289.png)

![JFourier[z_] = Series[With[{o = 100},
(1 + 240 Sum[DivisorSigma[3, n] q^n, {n, o}])^3/(q Product[(1 - q^n)^24, {n, o}])],
{q, 0, 50}][[3]] Table[E^(2 k I \[Pi] z), {k, -1, 50}];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7cfb6c7fed90c801.png)

![path\[DoubleStruckCapitalC][z_, f_ : Identity] := With[{zL = f@ReIm[Accumulate[JFourier[z]/1729]]},
{Thickness[0.001], Opacity[0.2], Gray, Line[zL],
Opacity[0.8], PointSize[0.003], Blue, Point[Last[zL]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/3e6e3cc1e7c4f705.png)
![Normal[ResourceFunction["ModularTessellation"][{3}, "Compositions"] //.
{Function[\[FormalZ], \[FormalZ]] -> \[ScriptCapitalI], Function[\[FormalZ], -\[FormalZ]^(-1)] -> \[ScriptCapitalK], Function[\[FormalZ], \[FormalZ] - 1] -> \[ScriptCapitalL], Function[\[FormalZ], \[FormalZ] + 1] -> \[ScriptCapitalR]}] //
Column // TraditionalForm](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/46392ea6f09dfd61.png)
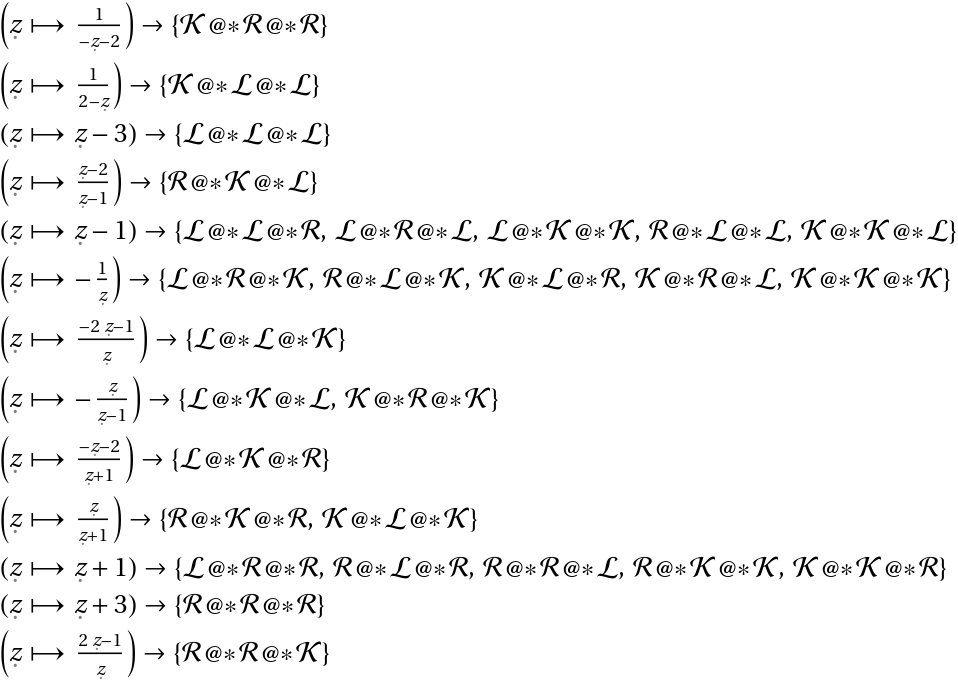
![ListLogPlot[ Reverse[({#1[[1]], #2} & @@@ Cases[Values[#], _Circle, \[Infinity]]) & /@ ResourceFunction["ModularTessellation"][16, "BoundingCircles"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/3c20231b03371aaf.png)
![coloredCircle3D[Circle[{x_, y_}, r_]] := With[{mp = {x, 4 Log10[1. r], y}}, {ColorData["DarkRainbow"][-Log10[1. r]],
Polygon[Append[#, mp] & /@ #], Black, Line[#]} &@
Partition[
Table[mp + r {Cos[\[CurlyPhi]], 0, Sin[\[CurlyPhi]]}, {\[CurlyPhi], 0., 2. Pi, 2 Pi/36}], 2, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/35b0faeab62e5323.png)
![Graphics3D[{EdgeForm[], coloredCircle3D /@ Cases[Values[
ResourceFunction["ModularTessellation"][{12}, "BoundingCircles"]], _Circle, \[Infinity]]}, Axes -> {True, False, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/02bc322c9ef0d163.png)
![Graphics[{Black, FordCircle /@ FareySequence[12],
Darker[Red], Values[ResourceFunction["ModularTessellation"][12, "BoundingCircles"]]},
PlotRange -> {{0, 1}, {0, 1/3}}, ImageSize -> Medium, Axes -> {True, False}, PlotRangeClipping -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/75bb1a79bec43c7a.png)

![Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, ResourceFunction["ModularTessellation"][
12] ] /.
Polygon[l_] :> Polygon[{#1, Log10[#2]} & @@@ l], PlotRange -> {{0, 2}, {-3, 1}}, AspectRatio -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/1a78b4afb6188ac3.png)

![With[{bw = MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, Select[#, Max[Norm /@ #[[1]]] <= 1 &] & /@ ResourceFunction["ModularTessellation"][12]]},
Graphics[{bw, GeometricTransformation[bw /. GrayLevel[g_] :>
GrayLevel[1 - g], ReflectionTransform[{0, 1}]]},
PlotRange -> 1, Background -> LightBlue]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/56b70e8de0d27132.png)

![Graphics[{RandomColor[], #} & /@ ResourceFunction["ModularTessellation"][12],
PlotRange -> {{-1, 1}, {0, 1}}, Background -> LightBlue]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/5d80bec3d2f43981.png)

![ridgePlot[p : Polygon[l_]] := Module[{rd = SignedRegionDistance[p], d}, d[x_Real, y_Real] := -rd[{x, y}];
Plot3D[d[x, y], {x, y} \[Element] p, Mesh -> False, PlotRange -> All, PlotPoints -> 60,
ColorFunction -> (Blend[{Black, Red}, #3^2] &), ColorFunctionScaling -> True]][[1]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/6e43efa445455750.png)
![Graphics3D[{#, GeometricTransformation[#, ReflectionTransform[{0, 1, 0}]]} &[
ridgePlot /@ Flatten[Select[#, Max[Norm /@ #[[1]]] <= 1 &] & /@ ResourceFunction["ModularTessellation"][5]]],
PlotRange -> All, Axes -> False, BoxRatios -> {1, 1, 0.3}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/53ffdecc82383704.png)

![Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, Values @ ResourceFunction["ModularTessellation"][
12, {"UnitDiskMappedApproximationPolygons", {2 I, -Pi/2}}] /. Polygon[l_] :> Polygon[nGonMap[3, #] & /@ l]],
PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/7f0647f3d92e4bde.png)

![Manipulate[
Graphics[MapIndexed[{GrayLevel[Mod[#2[[1]], 2]], #1} &, Values @ ResourceFunction["ModularTessellation"][
m, {"UnitDiskMappedApproximationPolygons", {\[Beta] . {1, I}, \[Theta]}}] ],
PlotRange -> 1],
{{m, 6}, Range[12], SetterBar},
{{\[Beta], {0, 2}}, {-3, 0.001}, {3, 3}},
{{\[Theta], -Pi/2}, -Pi, Pi}]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/3225350ace7c006d.png)

![gr = MapIndexed[{{Lighter[Blue, 0.2],
Lighter[Red, 0.2]}[[Mod[#2[[1]], 2] + 1]], #1} &, ResourceFunction["ModularTessellation"][6]];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/30b6c9c12459ac12.png)
![DynamicModule[{pt = {0, 1.3}},
Graphics[{gr, Yellow, Dynamic[
With[{l = Select[ReIm[#[pt . {1, I}] & /@ mtList], Max[Abs[#]] < 3 &]}, LL = l;
{Point[l], nf = Nearest[l]; {White, Line[{#, nf[#, 2][[-1]]} & /@ l]},
{Gray, Line[{#, nf[#, 3][[-1]]} & /@ l]},
{LightGray, Line[{nf[#, 2][[-1]], nf[#, 3][[-1]]} & /@ l]}}]],
Locator[
Dynamic[pt, (pt = {Min[0.5, Max[-0.5, #[[1]]]], Max[#[[2]], Sqrt[1 - #[[1]]^2]]}) &]]},
PlotRange -> {{-2, 2}, {0, 2}}, ImageSize -> 400]]](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/78b035a60a534fdc.png)

![circleData = SortBy[Cases[
Flatten[Values[
ResourceFunction["ModularTessellation"][{12}, "BoundingCircles"]]],
Circle[{_?(-1 <= # <= 1 &), _}, _]], N[#[[1, 1]]] &];](https://www.wolframcloud.com/obj/resourcesystem/images/a28/a2841112-ef14-406a-8ace-8e45535ab7a0/5110b604e4fafb16.png)