Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a numerically sorted list of abscissa-weight pairs for various modifications of Gaussian quadrature
ResourceFunction["ModifiedGaussianQuadratureWeights"][type,n] gives a list of the n pairs {xi,wi} of the n-point modified Gaussian formula for quadrature on the interval -1 to 1, where wi is the weight of the abscissa xi. | |
ResourceFunction["ModifiedGaussianQuadratureWeights"][type,n,{a,b}] rescales the Gaussian formula for the interval a to b. | |
ResourceFunction["ModifiedGaussianQuadratureWeights"][type,n,{a,b},prec] uses the working precision prec. |
| "AntiGaussian" | Laurie's anti-Gaussian quadrature formula |
| "Lobatto" | Gauss–Lobatto quadrature with both endpoints fixed, |
| "RadauLeft" | Gauss–Radau quadrature with left endpoint fixed, |
| "RadauRight" | Gauss–Radau quadrature with right endpoint fixed, |
The abscissas and weights for a 10-point Lobatto quadrature rule:
| In[1]:= |
| Out[1]= |
Lobatto quadrature rule over the interval 0 to 1:
| In[2]:= |
| Out[2]= |
Use the specified precision:
| In[3]:= |
| Out[3]= |  |
The abscissas and weights for a 10-point anti-Gaussian rule:
| In[4]:= |
| Out[4]= |
The "RadauLeft" and "RadauRight" rules are basically reflections of each other over the integration interval:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Use the modified Gaussian quadrature to approximate the area under a curve:
| In[7]:= |
Compare the results of the various modifications with classical Gaussian quadrature for a fixed n:
| In[8]:= | ![n = 5;
res = Table[
With[{gq = ResourceFunction["ModifiedGaussianQuadratureWeights"][type, n, {-0.5, 1.5}]}, Total[#2 f[#1] & @@@ gq]], {type, {"AntiGaussian", "Lobatto", "RadauLeft", "RadauRight"}}];
PrependTo[res, With[{gq = ResourceFunction["GaussianQuadratureWeights"][n, {-0.5, 1.5}]}, Total[#2 f[#1] & @@@ gq]]];
TableForm[
Transpose[{{"Gaussian", "AntiGaussian", "Lobatto", "RadauLeft", "RadauRight"}, res}], TableHeadings -> {None, {"Type", "Result"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c59/c59e92c0-3a65-4f10-8b4d-7dae0caf8ae8/1cc78f3d5752876f.png) |
| Out[8]= | 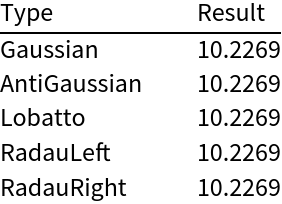 |
Compare with the result of NIntegrate by computing the absolute error:
| In[9]:= | ![ex = NIntegrate[f[x], {x, -0.5, 1.5}];
TableForm[
Transpose[{{"Gaussian", "AntiGaussian", "Lobatto", "RadauLeft", "RadauRight"}, Abs[res - ex]}], TableHeadings -> {None, {"Type", "Absolute Error"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c59/c59e92c0-3a65-4f10-8b4d-7dae0caf8ae8/2ad670dfd53b772e.png) |
| Out[9]= | 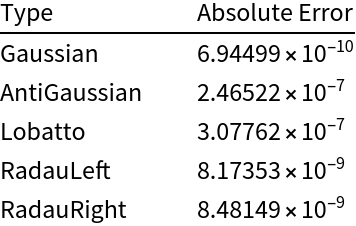 |
This work is licensed under a Creative Commons Attribution 4.0 International License