Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MobileAutomatonNonlocal

Source Notebook

Compute the evolution of a mobile automaton with nonlocal rules

Contributed by: Akshaj Devireddy

ResourceFunction["MobileAutomatonNonlocal"][rule,init,positions,t]

generates a list representing the evolution of the mobile automaton that measures the dependent cell indices positions relative to the active cell with the specified rule from initial condition init for t steps.

ResourceFunction["MobileAutomatonNonlocal"][rule,init,positions]

gives the result of evolving init using rule applied to the dependent cell indices positions for one step.

ResourceFunction["MobileAutomatonNonlocal"][rule]

is an operator form of ResourceFunction["MobileAutomatonNonlocal"] that corresponds to one step of evolution given a specified rule.

Details

The state for a mobile automaton is given in the form {{a1,a2,…}, n}, where the ai are values of cells and n is the position of the active cell.
The rules for a basic mobile automaton with nonlocal rules are given as a list of elements of the form {a-x,a0,a+x}→{ap,dn}, where a-x and a+x are the dependent cell positions relative to the active cell, ap is the new value of the active cell, and dn is its displacement.
Basic dependent cell positions are listed as {-x, 0, y}, where -x is the dependent cell position x cells to the left, y is the dependent cell position y cells to the right, and 0 represents the active cell position.
Other ways to express dependent cell positions are listed as {xi,xi+1... xk-1,xk}, where you can input multiple dependent cells rather than just 3.
The rules for a block mobile automaton with nonlocal rules are given as a list of elements of the form {a-x,a0,a+x}→{{ap-x,ap0,ap+x},dn}, where a-x and a+x are the dependent cell positions relative to the active cell, api are the new values for the block of cells and dn is the displacement of the active cell.
The rules for a generalized mobile automaton with nonlocal rules are given as a list of elements of the form {a-x,a0,a+x}→{ap,{dn-1,dn0,dn+1}}, where a-x and a+x are the dependent cell positions relative to the active cell, ap is the new value of the active cell and the dni are the new relative positions of the active cells.
The rules for a basic mobile automaton with non-local rules can be given as a pair of integers, in which case they will be decoded as specified in A New Kind of Science, page 887.
If the position of the active cell would be outside the range defined by the list of cells given, it is taken to be None.
ResourceFunction["MobileAutomatonNonlocal"][rule,init,positions,tsspec] supports the following time specifications tspec:
tall steps 0 through t
{{t}}step t alone
{t1,t2}steps t1 through t2
{t1,t2,dt}steps t1,t1+dt,…

Examples

Basic Examples (2) 

Five steps in the evolution of a mobile automaton with dependent cells 3 cells away on either side:

In[1]:=
ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 22], 11}, {-3, 0, 3}, 5]
Out[1]=

Visualize 40 steps of evolution of the mobile automaton with non-local rules scanning 3 cells away to either side of the active cell:

In[2]:=
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 22], 11}, {-3, 0, 3}, 40], Mesh -> True]
Out[2]=

Scope (4) 

Use rule numbers to specify a mobile automaton rule:

In[3]:=
ResourceFunction[ "MobileAutomatonNonlocal"][{37, 54, {-2, 0, 2}}, {Table[0, 21], 10}, 5]
Out[3]=

Visualize the evolution using the resource function MobileAutomatonPlot:

In[4]:=
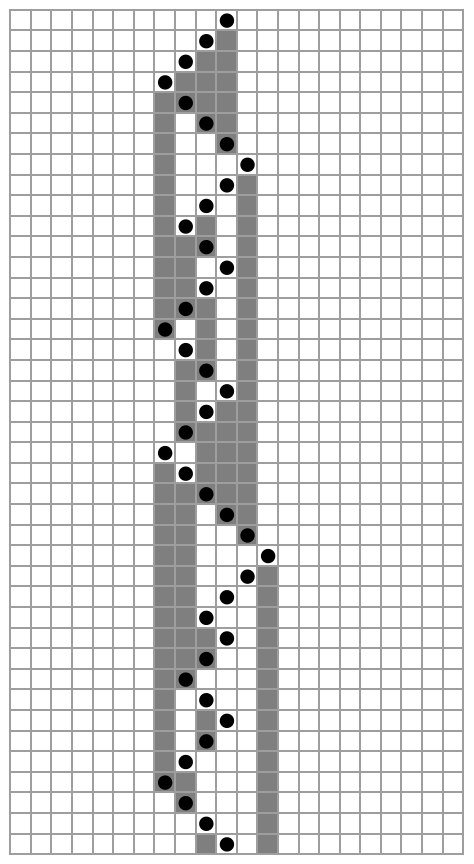
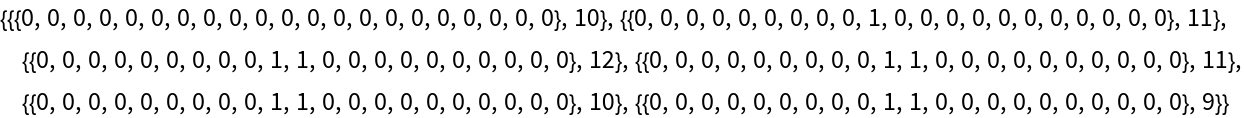
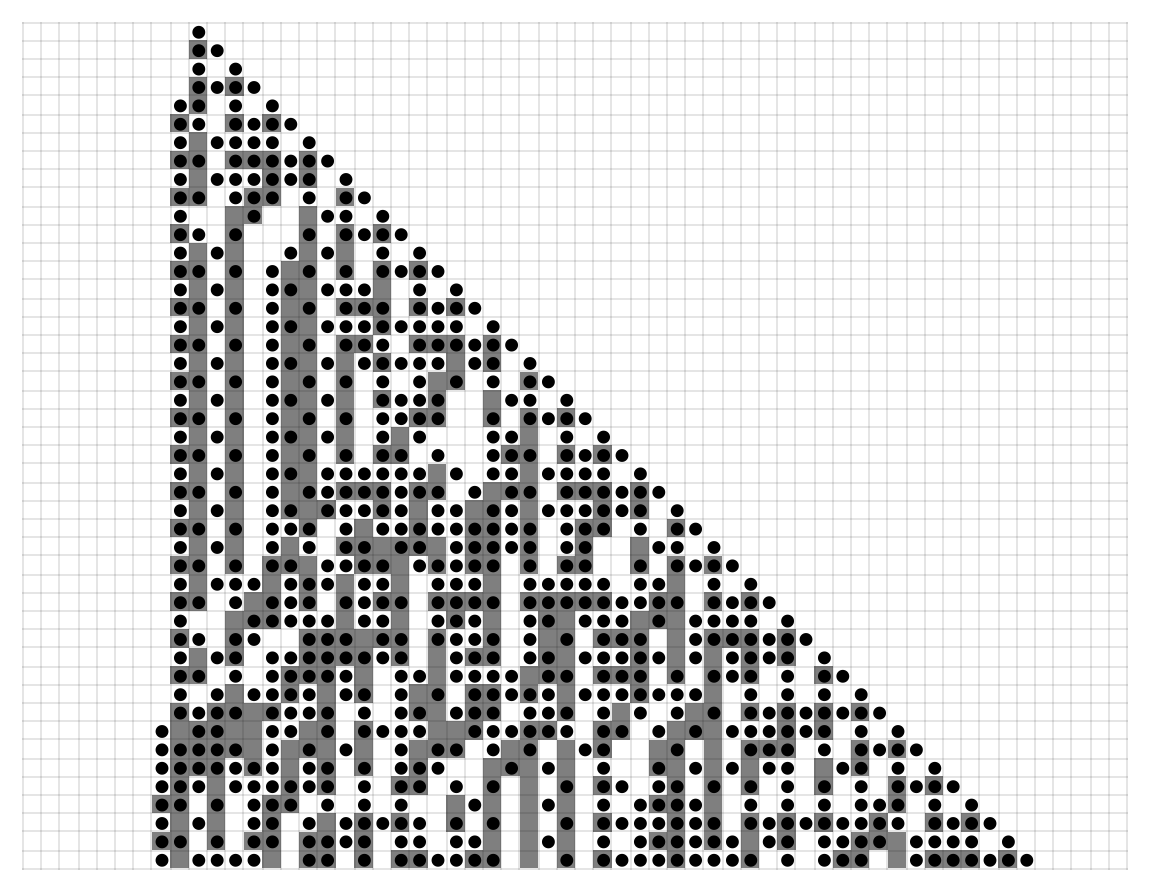
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction[ "MobileAutomatonNonlocal"][{37, 54, {-2, 0, 2}}, {Table[0, 40], 20}, 30], Mesh -> True]
Out[4]=

Show only the tenth step of an evolution:

In[5]:=
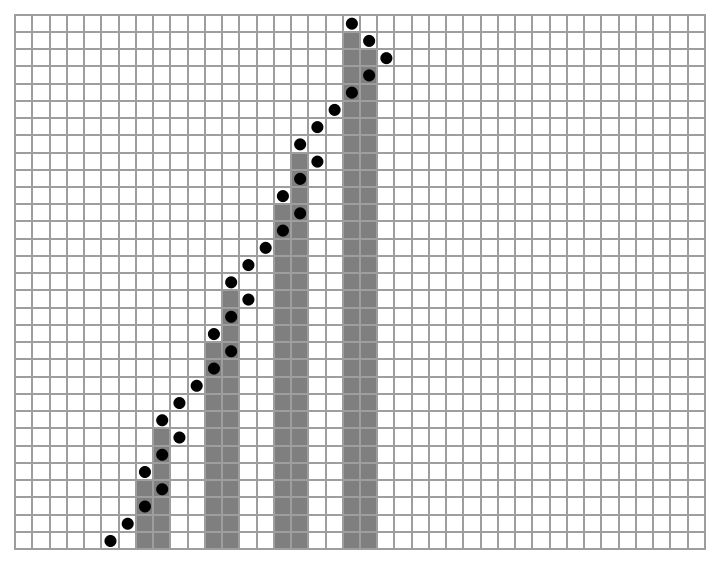
ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 40], 20}, {-2, 0, 3}, {{10}}]
Out[5]=

Show all steps from the fourth to the tenth, in steps of two:

In[6]:=
ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 40], 20}, {-2, 0, 3}, {4, 10, 2}]
Out[6]=

Properties and Relations (1) 

When the dependent cell positions are specified as {-1, 0, 1}, MobileAutomatonNonLocal emulates MobileAutomaton because the dependent cells are its immediate neighbors:

In[7]:=
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 20], 10}, {-1, 0, 1}, 20], Mesh -> True]
Out[7]=
In[8]:=
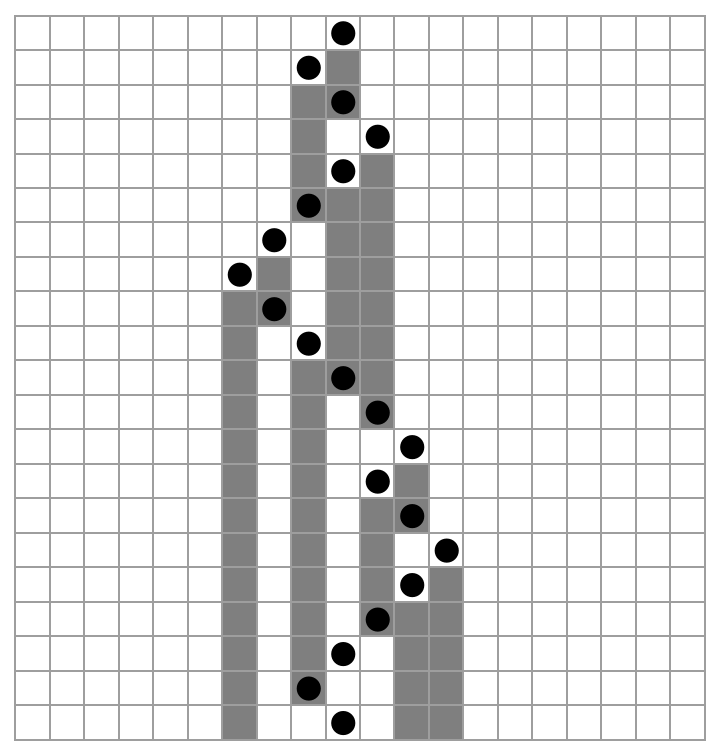
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 20], 10}, 20], Mesh -> True]
Out[8]=

Possible Issues (1) 

When the active cell goes out of the defined region its position is given as None:

In[9]:=
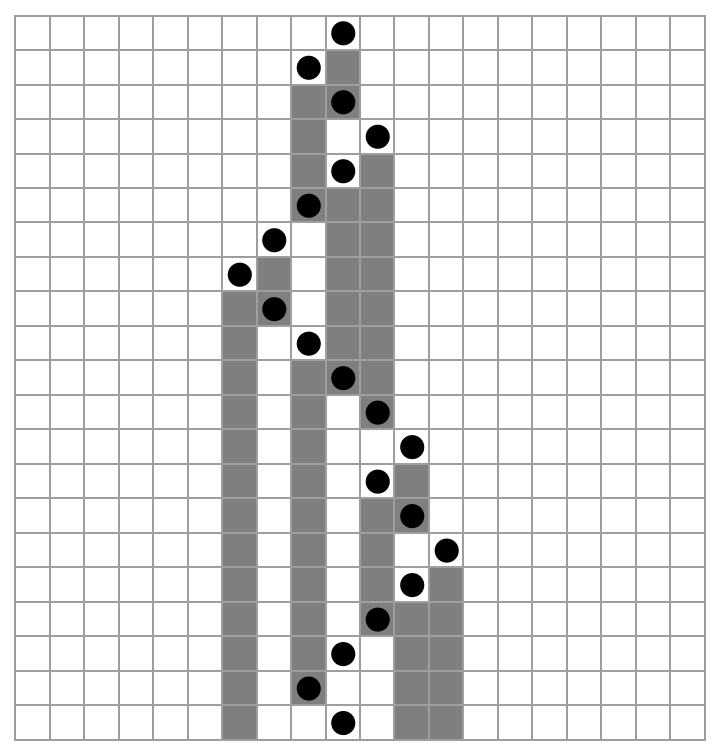
ResourceFunction[ "MobileAutomatonNonlocal"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {Table[0, 7], 3}, {-2, 0, 3}, 10]
Out[9]=

Neat Examples (3) 

We have rules that create more than one active cell here. We are testing same rules with different ranges of dependent cells:

In[10]:=
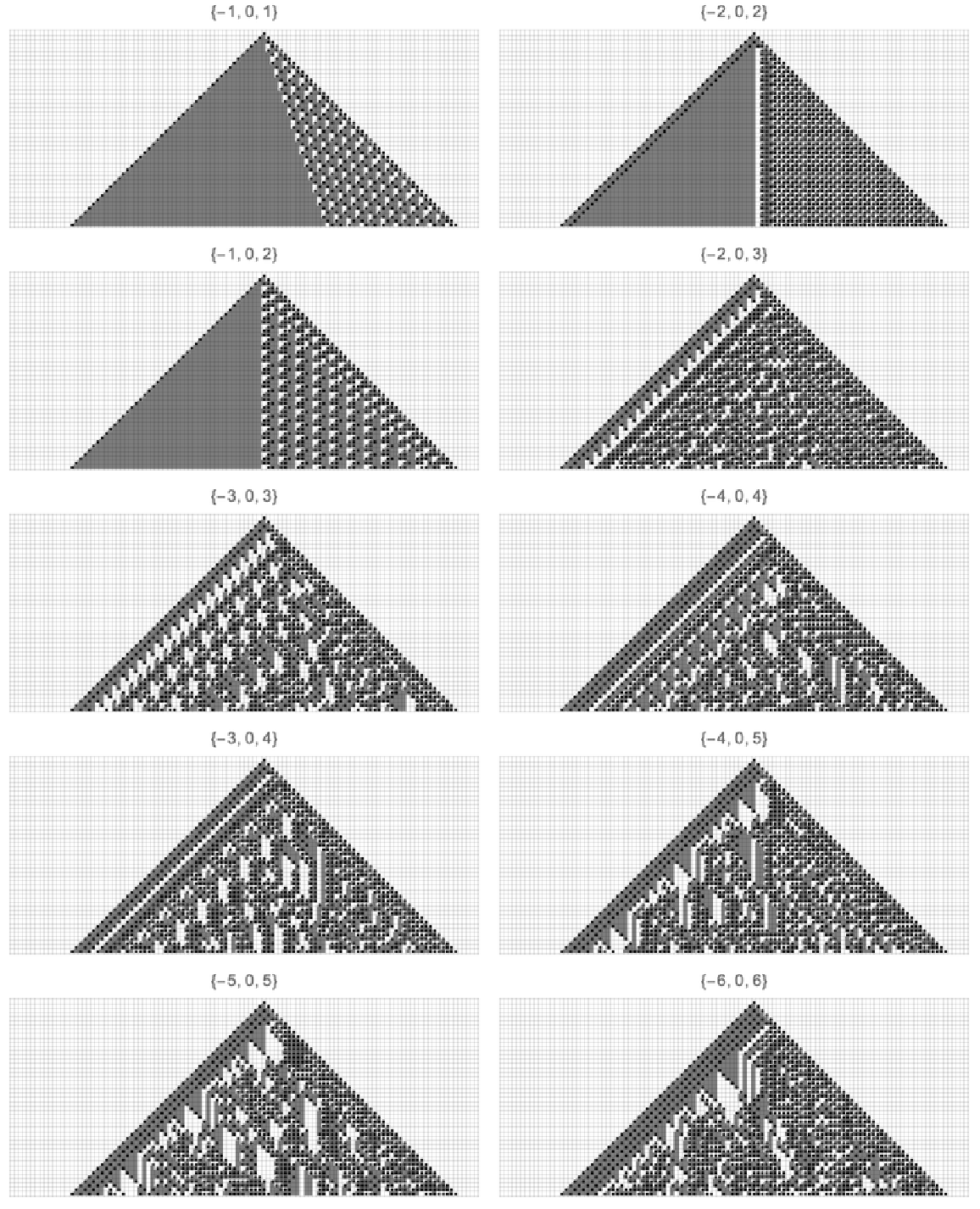
With[{rule = {{0, 0, 0} -> {1, {1, -1}}, {0, 0, 1} -> {1, {-1}}, {0, 1, 0} -> {1, {1, -1}}, {0, 1, 1} -> {1, {-1}}, {1, 0, 0} -> {1, {1, 0}}, {1, 0, 1} -> {1, {1}}, {1, 1, 0} -> {0, {1}}, {1, 1, 1} -> {0, {1}}}, dependentCellRanges = {{{-1, 0, 1}, {-2, 0, 2}}, {{-1, 0, 2}, {-2, 0, 3}}, {{-3, 0, 3}, {-4, 0, 4}}, {{-3, 0, 4}, {-4, 0, 5}}, {{-5, 0, 5}, {-6, 0, 6}}}}, Column[Table[ Row[ResourceFunction["MobileAutomatonPlot"][ ResourceFunction["MobileAutomatonNonlocal"][ rule, {Table[0, {110}], {60}}, #, 45], Mesh -> True, ColorRules -> {1 -> Black, 0 -> White}, MeshStyle -> Opacity[0.1], PlotLabel -> #, ImageSize -> Medium] & /@ i], {i, dependentCellRanges}]]]
Out[10]=

Plotting number of active cells over time for each of the mobile automata above:

In[11]:=
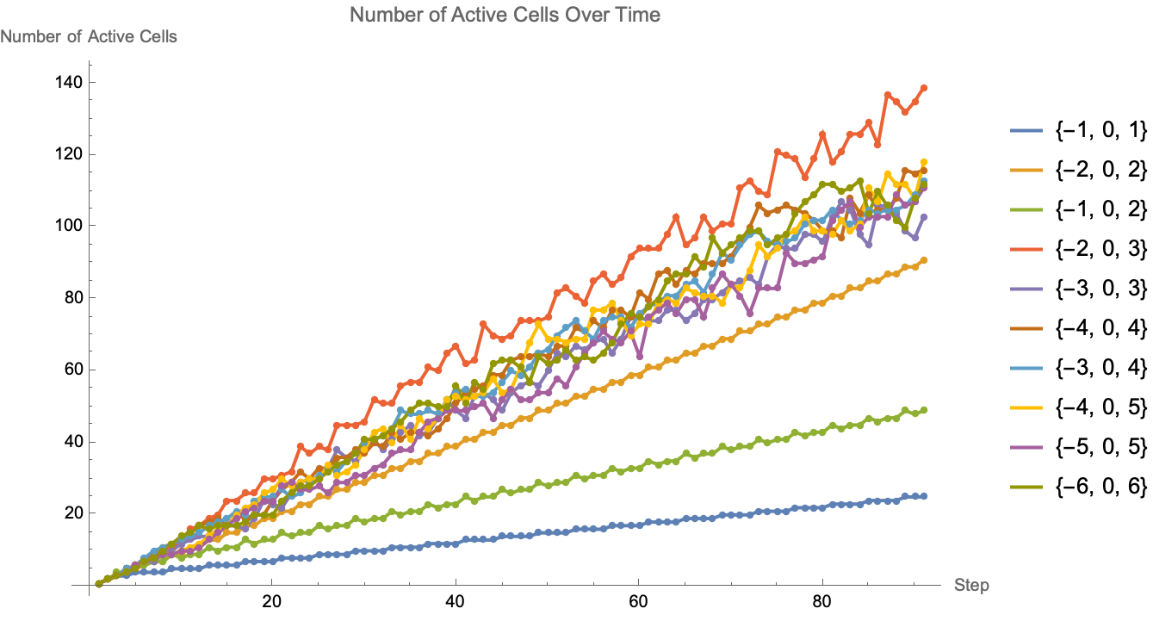
activeCellsOverTime[step_] := Module[{list, numberOfActiveCells}, list = step[[All, 2]]; numberOfActiveCells = Length /@ list] ListLinePlot[ activeCellsOverTime[ ResourceFunction[ "MobileAutomatonNonlocal"][{{0, 0, 0} -> {1, {1, -1}}, {0, 0, 1} -> {1, {-1}}, {0, 1, 0} -> {1, {1, -1}}, {0, 1, 1} -> {1, {-1}}, {1, 0, 0} -> {1, {1, 0}}, {1, 0, 1} -> {1, {1}}, {1, 1, 0} -> {0, {1}}, {1, 1, 1} -> {0, {1}}}, {Table[0, {200}], {100}}, #, 90]] & /@ {{-1, 0, 1}, {-2, 0, 2}, {-1, 0, 2}, {-2, 0, 3}, {-3, 0, 3}, {-4, 0, 4}, {-3, 0, 4}, {-4, 0, 5}, {-5, 0, 5}, {-6, 0, 6}}, AxesLabel -> {"Step", "Number of Active Cells"}, PlotLabel -> "Number of Active Cells Over Time", Mesh -> All, ImageSize -> Large, PlotLegends -> {"{-1, 0, 1}", "{-2, 0, 2}", "{-1, 0, 2}", "{-2, 0, 3}", "{-3, 0, 3}", "{-4, 0, 4}", "{-3, 0, 4}", "{-4, 0, 5}", "{-5, 0, 5}", "{-6, 0, 6}"}]
Out[12]=

Plotting mobile automata with 4 dependent cells positioned 3 cells to the left, 1 cell to the left, the active cell itself, and 2 cells to the right:

In[13]:=
rule = {{0, 0, 0, 0} -> {1, {1, 0}}, {0, 0, 0, 1} -> {0, {0}}, {0, 0, 1, 0} -> {0, {0}}, {0, 0, 1, 1} -> {1, {-1}}, {0, 1, 0, 0} -> {0, {1, -1}}, {0, 1, 0, 1} -> {1, {1}}, {0, 1, 1, 0} -> {0, {-1}}, {0, 1, 1, 1} -> {1, {1, -1}}, {1, 0, 0, 0} -> {1, {-1, 1}}, {1, 0, 0, 1} -> {1, {1}}, {1, 0, 1, 0} -> {1, {}}, {1, 0, 1, 1} -> {0, {0, 1}}, {1, 1, 0, 0} -> {0, {1}}, {1, 1, 0, 1} -> {0, {0}}, {1, 1, 1, 0} -> {0, {0, 1}}, {1, 1, 1, 1} -> {1, {-1}}}; ResourceFunction["MobileAutomatonPlot"][ ResourceFunction["MobileAutomatonNonlocal"][ rule, {Table[0, {60}], {10}}, {-3, -1, 0, 2}, 45], Mesh -> True, MeshStyle -> Opacity[.1], ImageSize -> Large, ColorRules -> {1 -> Black, 0 -> White}]
Out[13]=

Publisher

Akshaj Devireddy

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 15 July 2024

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science

Related Resources

License Information