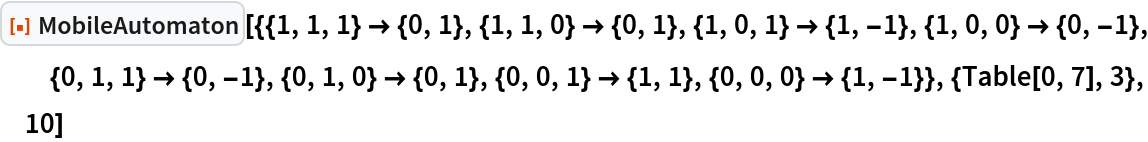Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MobileAutomaton

Source Notebook

Compute the evolution of a mobile automaton

Contributed by: Stephen Wolfram and Jan Mangaldan

ResourceFunction["MobileAutomaton"][rule,init,t]

generates a list representing the evolution of the mobile automaton or block mobile automaton with the specified rule from initial condition init for t steps.

ResourceFunction["MobileAutomaton"][rule,init]

gives the result of evolving init for one step.

ResourceFunction["MobileAutomaton"][rule]

is an operator form of ResourceFunction["MobileAutomaton"] that corresponds to one step of evolution.

Details

The state for a mobile automaton is given in the form {{a1,a2,…}, n}, where the ai are values of cells and n is the position of the active cell.
The rules for a basic mobile automaton are given as a list of elements of the form {a-1,a0,a+1}→{ap,dn}, where ap is the new value of the active cell and dn is its displacement.
The rules for a block mobile automaton are given as a list of elements of the form {a-1,a0,a+1}→{{ap-1,ap0,ap+1},dn}, where the api are the new values for the block of cells and dn is the displacement of the active cell.
The rules for a generalized mobile automaton are given as a list of elements of the form {a-1,a0,a+1}→{ap,{dn-1,dn0,dn+1}}, where ap is the new value of the active cell and the dni are the new relative positions of the active cells.
The rules for a basic mobile automaton can be given as a pair of integers, in which case they will be decoded as specified in A New Kind of Science, page 887.
If the position of the active cell would be outside the range defined by the list of cells given, it is taken to be None.
ResourceFunction["MobileAutomaton"][rule,init,tspec] supports the following time specifications tspec:
tall steps 0 through t
{{t}}step t alone
{t1,t2}steps t1 through t2
{t1,t2,dt}steps t1,t1+dt,…

Examples

Basic Examples (2) 

Five steps in the evolution of the mobile automaton from A New Kind of Science, page 71:

In[1]:=
ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 11], 5}, 5]
Out[1]=

Visualize 60 steps of evolution of the mobile automaton:

In[2]:=
ArrayPlot[ ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> { 1, -1}}, {ConstantArray[0, 41], 20}, 60][[All, 1]]]
Out[2]=

Scope (4) 

Use rule numbers to specify a mobile automaton rule:

In[3]:=
ResourceFunction["MobileAutomaton"][{35, 57}, {Table[0, 21], 10}, 5]
Out[3]=

Visualize the evolution using the resource function MobileAutomatonPlot:

In[4]:=
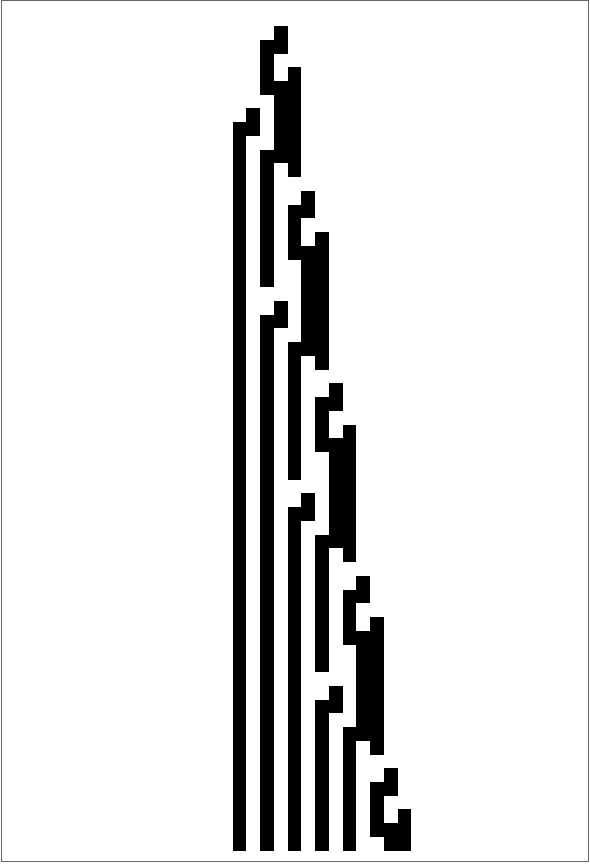
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction["MobileAutomaton"][{35, 57}, {Table[0, 21], 10}, 60], Mesh -> True]
Out[4]=

Show only the fifth step of an evolution:

In[5]:=
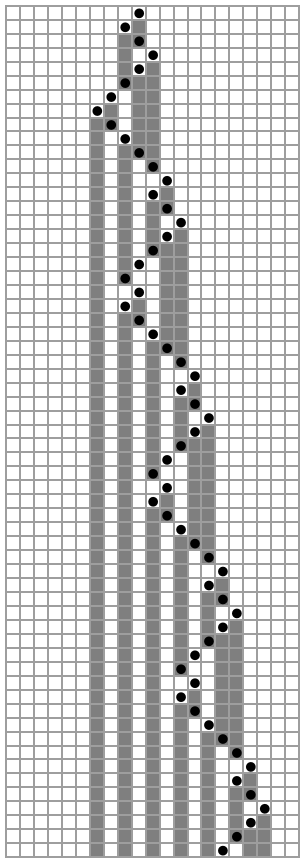
ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 11], 5}, {{5}}]
Out[5]=

Show all steps from the first to the fifth, in steps of two:

In[6]:=
ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {0, 1}, {1, 1, 0} -> {0, 1}, {1, 0, 1} -> {1, -1}, {1, 0, 0} -> {0, -1}, {0, 1, 1} -> {0, -1}, {0, 1, 0} -> {0, 1}, {0, 0, 1} -> {1, 1}, {0, 0, 0} -> {1, -1}}, {ConstantArray[0, 11], 5}, {1, 5, 2}]
Out[6]=

Evolution of the generalized mobile automaton from A New Kind of Science, page 73:

In[7]:=
ArrayPlot[ ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {{0, 0, 0}, -1}, {1, 1, 0} -> {{1, 0, 1}, -1}, {1, 0, 1} -> {{1, 1, 1}, 1}, {1, 0, 0} -> {{1, 0, 0}, 1}, {0, 1, 1} -> {{0, 0, 0}, 1}, {0, 1, 0} -> {{0, 1, 1}, -1}, {0, 0, 1} -> {{1, 0, 1}, 1}, {0, 0, 0} -> {{1, 1, 1}, 1}}, {ConstantArray[0, 41], 20}, 60][[All, 1]]]
Out[7]=

Position of the active cell in the generalized mobile automaton:

Out[7]=

Use the resource function MobileAutomatonPlot to visualize the evolution:

In[8]:=
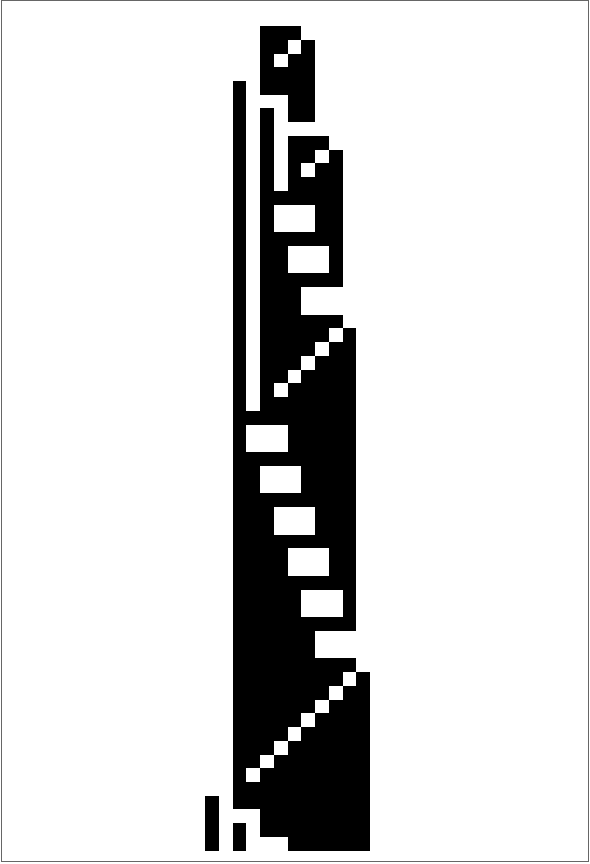
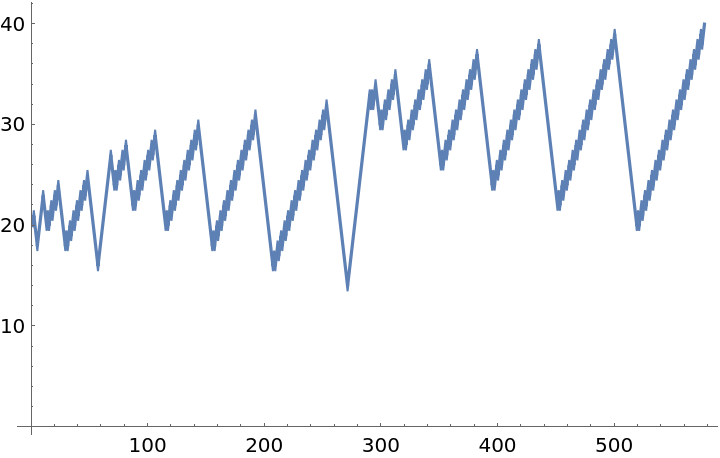
ResourceFunction["MobileAutomatonPlot"][ ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {{0, 0, 0}, -1}, {1, 1, 0} -> {{1, 0, 1}, -1}, {1, 0, 1} -> {{1, 1, 1}, 1}, {1, 0, 0} -> {{1, 0, 0}, 1}, {0, 1, 1} -> {{0, 0, 0}, 1}, {0, 1, 0} -> {{0, 1, 1}, -1}, {0, 0, 1} -> {{1, 0, 1}, 1}, {0, 0, 0} -> {{1, 1, 1}, 1}}, {ConstantArray[0, 21], 10}, 60], Mesh -> True]
Out[8]=

Color the active cell red:

In[9]:=
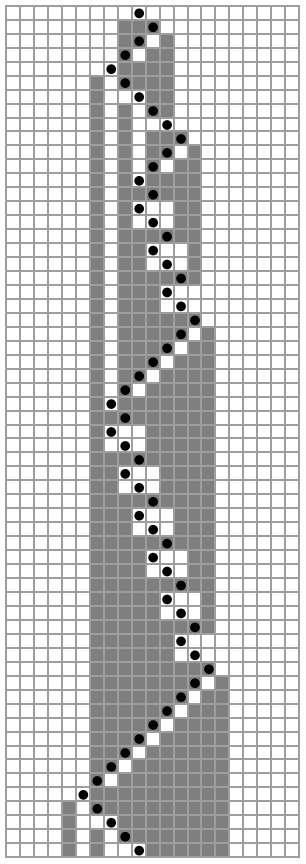
ArrayPlot[ MapAt[RGBColor[0.711529, 0.181058, 0.] &, #1, #2] & @@@ ResourceFunction[ "MobileAutomaton"][{{1, 1, 1} -> {{0, 0, 0}, -1}, {1, 1, 0} -> {{1, 0, 1}, -1}, {1, 0, 1} -> {{1, 1, 1}, 1}, {1, 0, 0} -> {{1, 0, 0}, 1}, {0, 1, 1} -> {{0, 0, 0}, 1}, {0, 1, 0} -> {{0, 1, 1}, -1}, {0, 0, 1} -> {{1, 0, 1}, 1}, {0, 0, 0} -> {{1, 1, 1}, 1}}, {ConstantArray[0, 41], 20}, 60]]
Out[9]=

Evolution of the generalized mobile automaton from A New Kind of Science, page 76:

In[10]:=
ArrayPlot[ ResourceFunction[ "MobileAutomaton"][{{0, 0, 0} -> {1, {1, -1}}, {0, 0, 1} -> {1, {-1}}, {0, 1, 0} -> {1, {1, -1}}, {0, 1, 1} -> {1, {-1}}, {1, 0, 0} -> {1, {1, 0}}, {1, 0, 1} -> {1, {1}}, {1, 1, 0} -> {0, {1}}, {1, 1, 1} -> {0, {1}}}, {ConstantArray[0, 43], {22}}, 20][[All, 1]]]
Out[10]=

Color the active cells red:

In[11]:=
ArrayPlot[ MapAt[RGBColor[0.711529, 0.181058, 0.] &, #1, List /@ #2] & @@@ ResourceFunction[ "MobileAutomaton"][{{0, 0, 0} -> {1, {1, -1}}, {0, 0, 1} -> { 1, {-1}}, {0, 1, 0} -> {1, {1, -1}}, {0, 1, 1} -> {1, {-1}}, {1, 0, 0} -> {1, {1, 0}}, {1, 0, 1} -> {1, {1}}, {1, 1, 0} -> { 0, {1}}, {1, 1, 1} -> {0, {1}}}, {ConstantArray[0, 43], {22}}, 20]]
Out[11]=

Possible Issues (1) 

When the active cell goes out of the defined region, a message is issued, and its position is given as None:

Out[11]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.1.0 – 19 July 2021

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science

Related Resources

License Information