Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MinimumVolumeEllipsoid

Source Notebook

Find the minimum-volume enclosing ellipsoid of a set of points

Contributed by: Jan Mangaldan

ResourceFunction["MinimumVolumeEllipsoid"][{p1,p2,…}]

gives the minimum-volume enclosing ellipsoid of the points p1,p2,….

Details and Options

The minimum-volume enclosing ellipsoid is also known as the Löwner ellipsoid or Löwner–John ellipsoid.
The minimum-volume enclosing ellipsoid is the smallest ellipsoid that includes the points pi.
The result is returned as an Ellipsoid.
ResourceFunction["MinimumVolumeEllipsoid"] takes the following options:
MaxIterations100maximum number of iterations to use
ToleranceAutomatictolerance for accepting an enclosing ellipsoid

Examples

Basic Examples (2) 

A minimum volume ellipse:

In[1]:=
pts = RandomReal[{-1, 1}, {50, 2}];
In[2]:=
ResourceFunction["MinimumVolumeEllipsoid"][pts]
Out[2]=

The region is the smallest ellipse that includes the points:

In[3]:=
Graphics[{{Directive[Opacity[0.6, LightBlue]], %}, Point[pts]}]
Out[3]=

A minimum volume ellipsoid:

In[4]:=
pts = RandomReal[{-1, 1}, {50, 3}];
In[5]:=
ResourceFunction["MinimumVolumeEllipsoid"][pts]
Out[5]=

The region is the smallest ellipsoid that includes the points:

In[6]:=
Graphics3D[{{Directive[Opacity[0.6, LightBlue]], %}, Point[pts]}]
Out[6]=

Options (2) 

MaxIterations (1) 

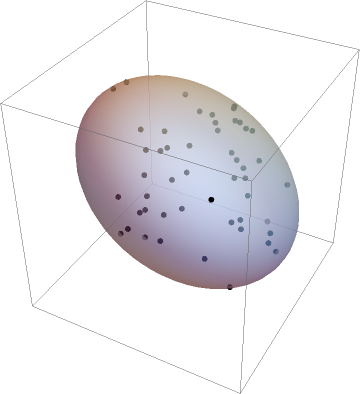Limit or increase the number of steps taken:

In[7]:=
pts = {{3, 10}, {6, 3}, {10, 2}, {2, 8}, {3, 3}};
In[8]:=
ResourceFunction["MinimumVolumeEllipsoid"][pts, MaxIterations -> 10]
Out[8]=

Tolerance (1) 

Increase or decrease the Tolerance:

In[9]:=
pts = {{3, 10}, {6, 3}, {10, 2}, {2, 8}, {3, 3}};
In[10]:=
ResourceFunction["MinimumVolumeEllipsoid"][pts, Tolerance -> 0.001]
Out[10]=

Applications (1) 

Find the minimum-volume enclosing ellipsoid for a 3D graphics object:

In[11]:=
graphics = \!\(\* Graphics3DBox[ {EdgeForm[None], GraphicsComplex3DBox[CompressedData[" 1:eJx1WGl0VtUVvUCVQZkkCeCK+CQMohWUOMRaea9QqqigKJQSsLxEwFW0ZuEY quATxLrsAqmtII6POoVolDpQRODehAhIBIOgIZDIExIQCRCQCNZQ6rfP/XTn QfLnW9k5OWeffYZ773debt7Nk1oqpS5voVQrhZ/oLye6mB8/g7+X1+oEcNUV O90EbgRX7fN2JHDfLd2bwFX1pFTYf5LxJez7n3OSvUv24bQQuLNo6y78/+aj tW4srktxvcMD4T/ceqAE/k8/Aj9B4dA0+KmZtSqBO28P3Bn3r8k/27tkz/5d 8s95uZRXuOnJNl4Cn/Ea/PhVOw/C38OrgKshNa8g3gd3HEl8mov/1yWBe5nF Bn7q077F/5l7zwa+6ddLYHcs7OTFcM346l+me+rnnyTO/jX5Zz6a+DB/TfzN xLdT4Gf0UdgFGbX1ib9HU2d3S+DhkoWHUKe2Sw/h/4Yr2EfrtsLeWXn+ER3z o8lPOOg54OHKLzfD77qGusSnd7Xg5qbUb8D/PsHZ3m3G3iX7JB/novHIX13X dw0+028VP21SwN9suAJ9ahoaoVsY9CmH3cCij13OK7PyO8S99voq5Lf0OOyN 6hNBx1m317ixuJrisj6a9Eni6p/uV9CnsF0D26vJuYfBL7cfdGX99Sn091L7 HUPc1epr2L//M0/EHS481f3SJ47Tpxxx37vkUFwfTfqwDpp0SOrmTegtfna+ 8TH7D3Vv6OmUiH/m6RJP80MP4H59Curud+2HPvUaBQ8bq9EnQdkFJ+Eu4ezH JT/JuMHho/skr1zU0xndtit0tj9m/aL/xvV3SX/245IfrqNLdTRq4Vkm8Xnz 44gb1m7cIfme6J7A/Wdu+AB5/TWlGH207ob0BB6+fR/yVePqoGsSd9KqilHH aW99hLyeXtjDEH+vXQX23E9zPWDJAVfi1vC8h08tB39VnrOH+UQjl21EfVd1 WIG8DssedqY9VYp+2pCD/aBG2P087829qEfdom3s3ytZVQV+dSv34/8ulP3p DWh9AHkN3P2iprimx2zhfUG3j5rg6xfh3DH3r9qOvDPHYJ7N3F2w91aM3RfP S1NeSTxyssX/lfua2KuC7fXwl14mc239q+wW2CNmyrdy/gyXOqrar2qgT8o5 6Fs13+aVs2AP+NR8uIX1DKaswNx5NzUWcB3VGX0rE3Ze+js7GPcnvPMF+L3l f44490hc76J8+FG9bqkDz3mWz8R/lOL/D312MF4vzfUi/i7x5/60fXJSf6Kf Y/3pPz+lCHhJ5WodwzXhzN9thr9L/Ll/XOqfZF289dWol3PajdsYj1YeE3xN 2nrwL3xG/Pf5V73stXLg0X7bVwcv3Y14J77dE+83l/rN223vLakKfoIulx3g fBNzCv/JOaW+0tRXPI92D9Swzon+h53tfxVIX5ll7bHHnMmLPo3PEeLaOeL+ 0dQ/PKfQLzmntE/g3+4T7mfY237muQNu547nBX+388K6adKN66KpLkl7PzcT uNcjc1mT+o7YW404w2Y16YdE3TXVnftEU5/wHsDvdg/w3oM/u/eCYjunzmeY U/VYbW28Lprqwvxd4s97AHhyD1g+zpu2TwbvLnVjuEs4962mvuV9At3sPmHd NOnGeWnKK7xwattEXHNdpszrY8F+/H30CNGtx+87A7/lO+z7MP3Z05rgj41G fSMnr0MC9/OXw0/UcAbwoM0u9HGUUdEq8XeVsrE+7t9rxr9H/s2uhZ3Zv3po BnCv4zftm/Bp16kunpdHeTEfQ3yiNmPlvlx6jdyvglux782XBR9Jf1WcAO/M Vofi9m4z9i7ZM0+PeLJuHunG+XqU70k8x/RuQN3/Xd3aI9xkhw2n5HkKe5fs VbA2FfHsj3d+DvZVsOa2NPB7tb3cj3tNAO51ngjcZLWX86KobG8T/NP2uOeo lwVX+T2BB51a4h3lj3O3Jf7u93wVePifDHmnlVz/Cepo8ajAYA/4dYI7V60U /IGhcp51qtmqYzzht6PwZHtN9t6oz4H71RmYB+eyTbiPM09NPJmPJj7MXxN/ k/R/RPgHo8Q/x3UprvOQ8A/fOVPuhxtqJG/LX42YXoF98Svhz/41+U/6MZM7 oC7+mbUn+dHkJ3qpFPfhaMoLj0NP+65kXBNu7HvBNBrcB5SbJe8pwjXjWfZ+ klUp58cTV33Bezt8bzHerV75DnmHkr0m+2i/nCNh5SzMc3he4Xb2EywpwPno O49j38f7PLqkf92p5uUnnPi4xIfjus3E1RQ36FYE3ZwODs5Tv83cd6FD/hbR 84pBODeDl6bi3Pbf/wHvO+fO4fBvcrbjHWB+Uw7cL3gdfpxvTns47keTn6Dy B3nXXO/gnPjxB3uJ+WjiE1k82LkW5104V3A1WOKqwmVbETe7I+L6Q6fD3nvk Adwzg9RG1MXTgpsR+VuA/26czN2O1+Xd+uF88FPXjJH3yB8EdyqfXgP7G3t8 Dp2zZgife/PF/x+zoAfz0cSH9dGkD+elKS/WWZPOzpUS1znxAM5df6rE9aaJ zur5rjjvzW7RObJ+zPptco8pEj/hpALhM2G+vP9HnivvMIsHtfMl30GCJ/X0 D+fLPWCm6Blukzo649ehLv6lUkdzQd/u0P/iD1AXf+kLeN+YfoL7+0QHM93i ZK/Jnv1r8s91RP2mSB05X035sj6a9OE+dKkPuR/g9y7pB+bvEv9kn5g7FkDP qFT6xH+xq/T/7JbQx5SPl3OqbVcbt5V8H7G2E+7p3oNyrnn9C1cjr2EfYo86 9YJHcxfDLrxGzrswcyD4BDnffy17c4fcly4V3Ls7DfzNTMGDu18S3cbOgl+/ 3UTc15ypgnu7BsNPUHYbcDVkgMSdt0belbe3lnetxcPgQexNZ7bgZvm1sreX D5BzqGyO3EuT+LN18OstFNy70hU+JTOx51Vqury7syy+YDDOQXV/d+BRy7Wi c8fvgYct+uP7SKeV4OHGVJnfYRcB90fnSf9c3gp1cYpHVcTjuhQ3TDkuef12 AO7lwZ4SfI/r7JFzNpqTje+LotsGbYvn61K+3rHu8OPkHZb+f3leVVw3l3SL HJk7Z/T2MtRp/ByJs8bid1XhvRcNlj7kvgKP15r2VTC3Be4Vaqj0lZq0DnHN ssV49wbLauoY94csRr95HwsevLFCvqdqnbEU/bNuwF7GwzkZS5HPKsG5Xi7X a5To74+chT3i/Vn0D3dbPSu+kHeOI3o6Vn9vQh3ev/4roj/70eSH+xZ52b7l ucDesHNhnm2U/Ta0/iD0GV65OV53zXUnPpr4qKJfAA+uljqq3LPk+787F0t/ vlKFOoZb5L2lMrvJvL/XUupy/OKD8blGvD4y18k9EG0oQL38muUV7Cfo3VL2 xlmXyLlPc4E+tHPB+bqUb5K/nydz7Y0U/uao9K235wl5v02XvuV6aaoX66BJ B55HxLXzaP4k/eONy8D5Eq6YKHu7r8Uf6Ym+Cm7KxPc8ST2jxu1l0CWyehJ/ txn+LvHnOYLu94xpEjfq0gt97v3Nxn1OdAsn3Yj7VVAkuvFcoy52rnk/IJ7d D7xvYW/3Le8l/L/dSxxXU1ze58jT7nPeq+Bv9yrrDB02WZ3tngluqIaeap/s Gd7zsLN7PkwrlD2wNUfe+fPkvuFbPBqei/uPmiG4mddf+iFvs+ylhrPle8fs 1lKvvUNw/oaTl0tdMiL5vvpRsQtPnyF69BI8apDvAcwwwcOx4ifolYk95Z0r fsyTEtcrPlu+FyoWf1HGYvGfnSP3tHd7Yo68FwR3zs/FPdAcF32Yv0v8Oa6m uMzfbYa/S/yTfMKyXLm/pWecxAf4eZOED+Wl+ZP0dJN6/h+ILPbH "], { Polygon3DBox[CompressedData[" 1:eJwNw4s/GgEAAGB1uaSz23bTauY4V+1SnE1L4fIoSuURhdZmvSxE7MGYmR5X 9BQp5Hne/JXz/X4f5lkc9bDLysoenwJPWWyAUw4C3AoWj80F2JV8COKAEJ9T 9Qx+/uIl8qpa8FooelPzVlCL1gnqsQZcLEIkUvE7ESFrFNXIFXhTMwm3vMfR D60NZLNEKRUIUUWTDIE/KmREA0airXXyFrxWUKdqUyNSgmhE6lFMJMdhUgWr 1BoeC6ho7+iktF0qoL2b38Pp1bB0Som+r99gHDBpSbPBMggMDVMjLGDQOjpW brOPV0IT1KSj55O6zWk0mGFn1ecvU+wxrlZFfnW5RyiPl/CZLZrpb/5pv4ua 6QDtsx5qLgCBYLndNr8AdA/pJEhwccknNbIGe22O+XnHd6mPWPzx09n2a3kc WqGG7bYF/e8+g9ViIjH/qnsNCrCtY9U6xPsHd/ndGgtvbRlC1zGFFw/2/12d clMbM0rdgOGfldrc6HFw5qiJ2QBIdU7CaifhVQSX9OsmLKjvD4Uj0XCIjsW3 tqPxWCKZStOZWHQ7nM3QsZ1cOhWMhFOJWC63sxtJJd2ZbG5XmEzvhSL5/Syd j4bEW9G8OBpJ5nPCQiJXKOzTyb18IZ4o0PFNaqV4cFg8PCodn5ROj4tHZ+cX zOUVU7q+uTpnSjenxbPb0t31xT1TvH14vGSKDwf3j0zp5O4/euainQ== "]], Polygon3DBox[CompressedData[" 1:eJxNlnt0j3Ucx59nWRibuc1t09hymU0zto50RBfpJimSFlGJEtFFLtXpD6fO iTrdjjq6ON1UMkQhyTWKbkhtyrIxkRBRmkXv9/m+Ou2cvc7vu+f5fj7vz+37 PE+7URMGjU+IouhnUUckiXqirmggmojGoqkohEYilXvzxfvsSeXX/zfDJlk0 5/8UbFOwS2XdDJv52OSIruxNFwtEiWgt2oos0U0UiFaio2gh0rjnPZkij/tp +GmNXQk+bX+nGC0WiofEJcS7SDwiporbxH1ikrhVjBAPimvFPWKcuF9cJC4W i8UHoqcYLm4Rs8RIauraXi/6igtFH3GBGCruQMO+B4olaNh3b2JybIPEdfie JpaiMUQ8IO4SN5Lb3WIsOWaR04ciW9wkhomPxERxBTWwzuVisFiG7Vj2LaJG 7u295DtZXCp64KO/6CDGiMvEANGLGi/E53BsXbNr8NGSXKbRxyJyd33PFxPo xXJq/CS5TKU/zn2KGEUNXJ9icSU++1L7QeQ9gPgmE8OjYrroJx4W49GYhHZv fBXTG5+d+uJq+jGOOt5MzEPorc9UEj77oTmG3oym7467J3k5v6vo/RLqNRhf Q+jtUOLvE4U56oWd6+OZvR3642s5/b5BJEbhvE9BeyA1m0iPk8lhAvEsptfL iKeY/g2jlouwm0X/nhYzxDOsl9Lbx8QT9Mx1zWbta49Te/fA52sE9Z/O2ufn OfECvrLBa59/Pwee5773PQszxVPcG8l6Jr5XiI/FSvGJWCU+FXPFa2I117x+ Q6zBxnvXinVivdggPhOvipfERq5vEp/j5wvWm/G5mr0vii3YvI2P9fj+Ek1r fYWP1cTyupgjXiGHFfiwr6/FN+JdfNrXt2IrPu1rm5gnXkbD17eL78QO6jAb H7b9nrg24nsDtnPQXkNu27FdRW6zsd2C7x9EKRql5ORc3iOXt0QZOW3Bdic5 lZGDY/+xlg/bvoPuDtZz8VHG3pX4ci4/4dNab+KzjNg2EVMp9+ZRm63YrqPX 9rFLlEfh/blbVIhKsUfsFVVin/hF7BcHxK/ioPhNHBKHxRHxuzjK7zHxhzgu Tog/xV/ipPhbVItTokb8I06LMyKK9ScSxFmijkiMg+YBfFvr7Dho2HddrevF /2v4t77+T+J6gzhoWruh1slx0LR2itaNRCo6jeNwLRHtJnGwqSFP+7bPk7U0 /NtUNItDLM3R9L4j5JUWh5gT0YrIyWvXNebaGWrRIg429tUyDn2yT/cpCa1W cejToVq1b03Mh7nehpycS7rIEG3FOSIzDj3eg227OMyANey7PdpZcZiRXcTm fdlxiHE/s5FB3+z7ALNhDd9L57r32PYos5GN7+P0rZzZcAzWrmY29qJ5mjpl EHsCOdVB0xr7yDkd7Upqcog8y9FKopYNqO1utD0bFWha27NRxeyn0rOI2TzI TNTQ4yPMxElm2zNxilk/V+sOoqPoFIcYHau/5/JFZ/2fI7qIXOfo+ok8rbuK zlH4HnTNXLvz2Ge7fGY4hRnz3HQTBfTQvewueuDLcfgb1T7bROG70nEVWp9r hfi1TlEcvjfTmQvPXh4+05iDLmh2Io/G5FhEHP5WXUAdHEf7KHwj56Jh3xnU wjHkk1shNXOtqmrVtAO59CCOzCj4LCCO7lHQLKHGOcTWjVhdW+/pTi6ubSZz 6edKEXHlE0MVs3CMZ08BuVUzq47jvx7717nlUFvH0Ik8csgrhRq14CzlEpdr 25TcHJffU35v+DngZ4vPlM+Wn/F+1vsZ7me5z1AWM+nZ9HvM7+qd7PG9lsyt z43fcZvx7T2+15x7Plt+z3mP3zl+91RwNqzl9+YJNB3LQbQ2cc8xO1bv8Xt6 bRSeST6H27jmdSX3/C3iZ6z3WGsb57aCeyvRbkhsroFzd4z/AvVboWs= "]]}]}, Boxed->False, ImageSize->{175., Automatic}, ViewPoint->{1.3, -2.4, 2.}, ViewVertical->{0., 0., 2.667290522030783}]\);
In[12]:=
mesh = DiscretizeGraphics[graphics];
In[13]:=
Show[graphics, Graphics3D[{Opacity[0.5], ResourceFunction["MinimumVolumeEllipsoid"][ MeshCoordinates[mesh]]}]]
Out[13]=

Properties and Relations (2) 

Compare the result of MinimumVolumeEllipsoid with the bounding ellipse returned by BoundingRegion[pts,"FastEllipse"]:

In[14]:=
pts = RandomReal[{-1, 1}, {50, 2}];
In[15]:=
e1 = BoundingRegion[pts, "FastEllipse"]
Out[15]=
In[16]:=
e2 = ResourceFunction["MinimumVolumeEllipsoid"][pts]
Out[16]=
In[17]:=
{Area[e1], Area[e2]}
Out[17]=

Compare the result of MinimumVolumeEllipsoid with the bounding ellipsoid returned by BoundingRegion[pts,"FastEllipsoid"]:

In[18]:=
pts = RandomReal[{-1, 1}, {50, 3}];
In[19]:=
e1 = BoundingRegion[pts, "FastEllipsoid"]
Out[19]=
In[20]:=
e2 = ResourceFunction["MinimumVolumeEllipsoid"][pts]
Out[20]=
In[21]:=
{Volume[e1], Volume[e2]}
Out[21]=

Version History

  • 1.0.0 – 31 December 2020

Source Metadata

  • Citation:
    • Todd, M.J., Yıldırım, E.A., "On Khachiyan's algorithm for the computation of minimum-volume enclosing ellipsoids." Discrete Applied Mathematics, vol.155, no.13, pp. 1731-1744, 2007.
      DOI:10.1016/j.dam.2007.02.013

License Information