Function Repository Resource:

MinMaxRounded

Source Notebook

Get the minimum and maximum of a list rounded to a multiple

Contributed by: Sander Huisman

ResourceFunction["MinMaxRounded"][list]

gives the minimum and maximum of list, rounded down and up, respectively.

ResourceFunction["MinMaxRounded"][list,a]

gives the minimum and maximum of list, rounded down and up to a multiple of a.

ResourceFunction["MinMaxRounded"][list,a,{f,g}]

gives {f[Min[list],a],g[Max[list],a]}.

Details and Options

ResourceFunction["MinMaxRounded"] is used to find nice, readable numbers for the range of the values of a list.

ResourceFunction["MinMaxRounded"][list] gives {Floor[Min[list]],Ceiling[Max[list]]}.

ResourceFunction["MinMaxRounded"][list,a] gives {Floor[Min[list],a],Ceiling[Max[list],a]}.

Common values for {f,g} are:

{Floor,Ceiling}

minimum and maximum values are rounded "outward"

{Ceiling,Floor}

minimum and maximum values are rounded "inward"

{Round,Round}

minimum and maximum values are rounded to the closest value

Examples

Basic Examples (2)

Find the rounded-down minimum and rounded-up maximum for a list of values:

In[1]:=

Out[1]=

Find the minimum rounded down to a multiple of 5 and the maximum rounded up to a multiple of 5 for a list of values:

In[2]:=

Out[2]=

Scope (2)

By default, the minimum is rounded down and the maximum rounded up:

In[3]:=

Out[3]=

Round the minimum up and the maximum down:

In[4]:=

Out[4]=

Round the minimum and the maximum to the closest multiple of 5:

In[5]:=

Out[5]=

If the minimum is positive, return 0 and do not round the maximum:

In[6]:=

Out[6]=

Applications (1)

Find a "nice" plot range that includes all the data:

In[7]:=

Out[8]=

Possible Issues (1)

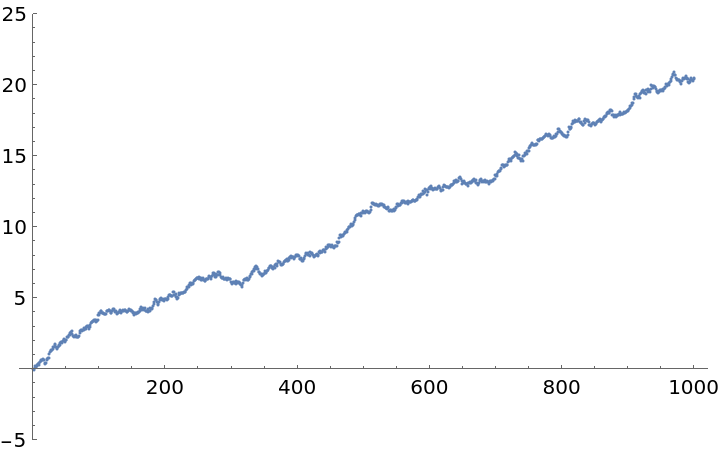An empty list returns :

In[9]:=

Out[9]=

Publisher

SHuisman

Version History

1.0.0 – 02 August 2019

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License