Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Metric
Represent a metric tensor (field) for a Riemannian or pseudo-Riemannian manifold
Contributed by:
Jonathan Gorard
ResourceFunction["MetricTensor"]["name",…] represents a named metric tensor "name". | |
ResourceFunction["MetricTensor"][{"name",…},…] represents a named parameterized metric tensor "name", with additional parameter(s) specified within a list. | |
ResourceFunction["MetricTensor"][d,…] represents a generic d-dimensional (symmetric) metric tensor. | |
ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],coords] transforms a specified ResourceFunction["MetricTensor"] into the new coordinate system coords. | |
ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],i1,i2] transforms a specified ResourceFunction["MetricTensor"] into one with new indices i1 and i2 (with True representing a covariant index and False representing a contravariant one), raising and lowering existing indices as necessary. | |
ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],coords,i1,i2] transforms a specified ResourceFunction["MetricTensor"] into one with new coordinate system coords and new indices i1 and i2 (with True representing a covariant index and False representing a contravariant one), raising and lowering existing indices as necessary. |
Details
Formally, a metric tensor is a (symmetric) bilinear form defined on the tangent space at a specified point of a manifold, and a metric tensor field associates a metric tensor to every such point in that manifold. Informally, the metric tensor generalizes the inner product operation in flat (Euclidean) spaces, thus allowing one to define distances and angles in a consistent way on manifolds with non-zero curvature.
Strictly speaking, ResourceFunction["MetricTensor"] typically represents a metric tensor field rather than a single metric tensor (this terminological ambiguity is commonplace in both geometry and physics, and ResourceFunction["MetricTensor"] generally does not make any such distinction).
By default, ResourceFunction["MetricTensor"][mat,coords,i1,i2] represents a metric tensor by a (symmetric) matrix representation mat in a given coordinate basis coords, such that the entries of mat transform either covariantly or contravariantly, or some mixture of the two, with respect to transformations of coords. The coordinates coords should be given as a list of coordinate symbols whose length is equal to the dimension of the matrix (and thus of the manifold). The indices i1 and i2 can either be set to True (covariant) or False (contravariant). By default, both indices are set to True (i.e. all components of the matrix transform covariantly).
ResourceFunction["MetricTensor"] performs all raising and lowering of indices automatically, as required. The inverse metric can be obtained by setting both indices to False (i.e. all components of the matrix transform contravariantly).
ResourceFunction["MetricTensor"] does not assume any particular number of dimensions for the underlying manifold (some in-built metrics, such as "Schwarzschild", assume a 1+3-dimensional spacetime, although others, such as "Minkowski", work in arbitrary numbers of dimensions). ResourceFunction["MetricTensor"] also does not assume any particular metric convention, although some in-built metrics (and some properties, such as "LorentzianConditions") implicitly assume a (-,+,+,+) signature. Finally, ResourceFunction["MetricTensor"] does not require the metric to be strictly symmetric (i.e. spin and torsion connections are also supported).
Based on the eigenvalues of the matrix representation of the metric tensor in covariant form, the underlying manifold will be classified by ResourceFunction["MetricTensor"] as either Riemannian (either all eigenvalues positive or all eigenvalues negative), pseudo-Riemannian (some eigenvalues positive and some eigenvalues negative), Lorentzian (all eigenvalues positive except for one negative, or eigenvalues negative except for one positive) or Indeterminate.
The property "RiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation are all strictly positive; "PseudoRiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix repreesentation are all non-zero; "LorentzianConditions" returns the conditions necessary to guarantee that the eigenvalue corresponding to the {1,0,0,…} eigenvector (if it exists) is negative, with all other eigenvalues being positive. Note that this is strictly less general than the behavior of properties such as "RiemannianQ" (described in the point above), since it assumes certain features of the metric signature.
ResourceFunction["MetricTensor"] implicitly keeps track of all known algebraic equivalences between tensor expressions, and can apply them for simplification purposes where necessary. Requesting any property with "Reduced" in its name has the effect of applying all known tensor equivalences and simplifying (note that this can have the effect of increasing computation time significantly).
When specifying a metric tensor, either using an in-built name or using an explicit matrix representation, ResourceFunction["MetricTensor"] allows one to omit the list of coordinates coords or the indices i1 and i2 (or both). If the list of coordinates coords is omitted, it is automatically populated either with {x0,x1,…} (in the general case), or with a list of coordinate names appropriate for the metric in question (in the case of in-built metrics). If the indices i1 and i2 are omitted, they are both automatically assumed to be True (covariant).
In ResourceFunction["MetricTensor"]["name",…] or ResourceFunction["MetricTensor"][{"name",…},…], the following named (in-built) metrics are supported:
| "Symmetric" | a generic 4-dimensional symmetric metric (whose matrix representation is populated with constants of the form gij=gji) |
| {"Symmetric",d} | a generic d-dimensional symmetric metric (whose matrix representation is populated with constants of the form gij=gji) |
| "SymmetricField" | a generic 4-dimensional symmetric metric tensor field (whose matrix representation is populated with functions of the chosen coordinates of the form gij=gji) |
| {"SymmetricField",d} | a generic d-dimensional symmetric metric tensor field (whose matrix representation is populated with functions of the chosen coordinates of the form gij=gji) |
| "Asymmetric" | a generic 4-dimensional asymmetric metric (whose matrix representation is populated with constants of the form gij≠gji) |
| {"Asymmetric",d} | a generic d-dimensional asymmetric metric (whose matrix representation is populated with constants of the form gij≠gji) |
| "AsymmetricField" | a generic 4-dimensional asymmetric metric tensor field (whose matrix representation is populated with functions of the chosen coordinates of the form gij≠gji) |
| {"AsymmetricField",d} | a generic d-dimensional asymmetric metric tensor field (whose matrix representation is populated with functions of the chosen coordinates of the form gij≠gji) |
| "Euclidean" | the metric for 3-dimensional flat/Euclidean space in Cartesian coordinates |
| {"Euclidean",d} | the metric for d-dimensional flat/Euclidean space in Cartesian coordinates |
| "Minkowski" | the metric for 4-dimensional (or 1+3-dimensional) flat/Minkowski spacetime in Cartesian coordinates |
| {"Minkowski",d} | the metric for d-dimensional (or 1+(d-1)-dimensional) flat/Minkowski spacetime in Cartesian coordinates |
| "Schwarzschild" | the metric describing the exterior spacetime geometry surrounding an uncharged, spherically-symmetric, non-rotating mass distribution (e.g. an uncharged, non-rotating black hole) in Schwarzschild/spherical polar coordinates, with purely symbolic mass "M" |
| {"Schwarzschild",M} | the metric describing the exterior spacetime geometry surrounding an uncharged, spherically-symmetric, non-rotating mass distribution (e.g. an uncharged, non-rotating black hole) in Schwarzschild/spherical polar coordinates, with numerical mass M |
| "IsotropicSchwarzschild" | the Schwarzschild metric represented in isotropic coordinates (i.e. the Cartesian-like coordinate system in which radial distances are defined such that light cones appear round), with purely symbolic mass "M" |
| {"IsotropicSchwarzschild",M} | the Schwarzschild metric represented in isotropic coordinates (i.e. the Cartesian-like coordinate system in which radial distances are defined such that light cones appear round), with numerical mass M |
| "EddingtonFinkelstein" | the Schwarzschild metric represented in Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to radial lightlike geodesics), with purely symbolic mass "M" |
| {"EddingtonFinkelstein",M} | the Schwarzschild metric represented in Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to radial lightlike geodesics), with numerical mass M |
| "IngoingEddingtonFinkelstein" | the Schwarzschild metric represented in ingoing Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to inward-traveling radial lightlike geodesics), with purely symbolic mass "M" |
| {"IngoingEddingtonFinkelstein",M} | the Schwarzschild metric represented in ingoing Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to inward-traveling radial lightlike geodesics), with numerical mass M |
| "OutgoingEddingtonFinkelstein" | the Schwarzschild metric represented in outgoing Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to outward-traveling radial lightlike geodesics), with purely symbolic mass "M" |
| {"OutgoingEddingtonFinkelstein",M} | the Schwarzschild metric represented in outgoing Eddington-Finkelstein coordinates (i.e. the coordinate system adapted to outward-traveling radial lightlike geodesics), with numerical mass M |
| "GullstrandPainleve" | the Schwarzschild metric represented in Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer from infinity), with purely symbolic mass "M" |
| {"GullstrandPainleve",M} | the Schwarzschild metric represented in Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer from infinity), with numerical mass M |
| "IngoingGullstrandPainleve" | the Schwarzschild metric represented in ingoing Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer, falling inwards from infinity), with purely symbolic mass "M" |
| {"IngoingGullstrandPainleve",M} | the Schwarzschild metric represented in ingoing Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer, falling inwards from infinity), with numerical mass M |
| "OutgoingGullstrandPainleve" | the Schwarzschild metric represented in outgoing Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer, falling outwards to infinity), with purely symbolic mass "M" |
| {"OutgoingGullstrandPainleve",M} | the Schwarzschild metric represented in outgoing Gullstrand-Painlevé coordinates (i.e. the coordinate system whose time coordinate follows the proper time of a free-falling observer, falling outwards to infinity), with numerical mass M |
| "KruskalSzekeres" | the Schwarzschild metric represented in Kruskal-Szekeres coordinates (i.e. the coordinate system that covers the entire spacetime manifold of the maximal analytic extension of the Schwarzschild solution), with purely symbolic mass "M" |
| {"KruskalSzekeres",M} | the Schwarzschild metric represented in Kruskal-Szekeres coordinates (i.e. the coordinate system that covers the entire spacetime manifold of the maximal analytic extension of the Schwarzschild solution), with numerical mass M |
| "Kerr" | the metric describing the exterior spacetime geometry surrounding an uncharged, axially-symmetric, rotating mass distribution (e.g. an uncharged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with purely symbolic mass "M" and purely symbolic angular momentum "J" |
| {"Kerr",M} | the metric describing the exterior spacetime geometry surrounding an uncharged, axially-symmetric, rotating mass distribution (e.g. an uncharged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with numerical mass M and purely symbolic angular momentum "J" |
| {"Kerr",M,J} | the metric describing the exterior spacetime geometry surrounding an uncharged, axially-symmetric, rotating mass distribution (e.g. an uncharged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with numerical mass M and numerical angular momentum J |
| "ReissnerNordstrom" | the metric describing the exterior spacetime geometry surrounding a charged, spherically-symmetric, non-rotating mass distribution (e.g. a charged, non-rotating black hole) in Schwarzschild/spherical polar coordinates, with purely symbolic (total) mass "M" and purely symbolic electric charge "Q" |
| {"ReissnerNordstrom",M} | the metric describing the exterior spacetime geometry surrounding a charged, spherically-symmetric, non-rotating mass distribution (e.g. a charged, non-rotating black hole) in Schwarzschild/spherical polar coordinates, with numerical (total) mass M and purely symbolic electric charge "Q" |
| {"ReissnerNordstrom",M,Q} | the metric describing the exterior spacetime geometry surrounding a charged, spherically-symmetric, non-rotating mass distribution (e.g. a charged, non-rotating black hole) in Schwarzschild/spherical polar coordinates, with numerical (total) mass M and numerical electric charge Q |
| "KerrNewman" | the metric describing the exterior spacetime geometry surrounding a charged, axially-symmetric, rotating mass distribution (e.g. a charged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with purely symbolic (total) mass "M", purely symbolic angular momentum "J" and purely symbolic electric charge "Q" |
| {"KerrNewman",M} | the metric describing the exterior spacetime geometry surrounding a charged, axially-symmetric, rotating mass distribution (e.g. a charged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with numerical (total) mass M, purely symbolic angular momentum "J" and purely symbolic electric charge "Q" |
| {"KerrNewman",M,J} | the metric describing the exterior spacetime geometry surrounding a charged, axially-symmetric, rotating mass distribution (e.g. a charged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with numerical (total) mass M, numerical angular momentum J and purely symbolic electric charge "Q" |
| {"KerrNewman",M,J,Q} | the metric describing the exterior spacetime geometry surrounding a charged, axially-symmetric, rotating mass distribution (e.g. a charged, spinning black hole) in Boyer-Lindquist/oblate spheroidal coordinates, with numerical (total) mass M, numerical angular momentum J and numerical electric charge Q |
| "Godel" | the metric describing the spacetime geometry of a rotating, dust-filled universe in Gödel's Cartesian-like coordinates, with purely symbolic angular velocity "" |
| {"Godel",ω} | the metric describing the spacetime geometry of a rotating, dust-filled universe in Gödel's Cartesian-like coordinates, with numerical angular velocity ω |
| "FLRW" | the metric describing the spacetime geometry of a homogeneous, isotropic universe which is either contracting or expanding in spherical polar coordinates, with purely symbolic global curvature "k" and purely symbolic scale factor "a" (treated as a function of coordinate time) |
| {"FLRW",k} | the metric describing the spacetime geometry of a homogeneous, isotropic universe which is either contracting or expanding in spherical polar coordinates, with numerical global curvature k and purely symbolic scale factor "a" (treated as a function of coordinate time) |
| {"FLRW",k,a} | the metric describing the spacetime geometry of a homogeneous, isotropic universe which is either contracting or expanding in spherical polar coordinates, with numerical global curvature k and numerical scale factor a (treated as a function of coordinate time) |
Calling ResourceFunction["MetricTensor"][] returns a list of all named (in-built) metrics.
If the function succeeds in constructing the specified metric tensor, it will return a ResourceFunction["MetricTensor"] expression.
Calling ResourceFunction["MetricTensor"][…][i,j] returns the entry in the i-th column and the j-th row of the (covariant) matrix representation of the metric tensor; similarly, ResourceFunction["MetricTensor"][…][i,All] and ResourceFunction["MetricTensor"][All,j] return the complete i-th row and the complete j-th column of the (covariant) matrix representation, respectively.
Calling ResourceFunction["MetricTensor"][…][v] computes the length of the tangent vector v using the given metric tensor. Calling ResourceFunction["MetricTensor"][…][v1,v2] computes the angle between vectors v1 and v2 using the given metric tensor.
Calling ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],coords] has the effect of transforming the metric tensor to the new coordinate system coords. Calling ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],i1,i2] has the effect of raising and lowering appropriate indices of the metric tensor to match i1 and i2 (with True representing lowered/covariant and False representing raised/contravariant). Calling ResourceFunction["MetricTensor"][ResourceFunction["MetricTensor"][…],coords,i1,i2] has the effect of performing both transformations simultaneously.
By default, ResourceFunction["MetricTensor"] keeps track of the positions of all indices implicitly and performs all raising and lowering operations automatically, as required for a given computation.
In ResourceFunction["MetricTensor"], the following properties are supported:
| "MatrixRepresentation" | metric tensor represented in explicit matrix form |
| "ReducedMatrixRepresentation" | metric tensor represented in explicit matrix form, modulo all tensor equivalences |
| "Coordinates" | list of coordinate symbols for the metric tensor |
| "CoordinateOneForms" | list of differential 1-form symbols for the coordinates of the metric tensor |
| "Indices" | list of booleans specifying whether each index is lowered/covariant (True) or raised/contravariant (False) |
| "CovariantQ" | whether the metric tensor is covariant (i.e. both indices are lowered/covariant) |
| "ContravariantQ" | whether the metric tensor is contravariant (i.e. both indices are raised/contravariant) |
| "MixedQ" | whether the metric tensor is mixed (i.e. one index is lowered/covariant and one index is raised/contravariant) |
| "Symbol" | symbolic representation of the metric tensor with appropriately raised/lowered indices |
| "Dimensions" | number of dimensions of the manifold/spacetime represented by the metric tensor |
| "SymmetricQ" | whether the metric tensor is symmetric (i.e. is represented by a symmetric matrix in covariant form) |
| "DiagonalQ" | whether the metric tensor is diagonal (i.e. is represented by a diagonal matrix in covariant form) |
| "Signature" | list of +1s and -1s designating the signature of the metric tensor (+1 for each positive eigenvalue, -1 for each negative eigenvalue) |
| "RiemannianQ" | whether the metric tensor describes a Riemannian manifold (i.e. all eigenvalues have the same sign) |
| "PseudoRiemannianQ" | whether the metric tensor describes a pseudo-Riemannian manifold (i.e. all eigenvalues are non-zero, but not all have the same sign) |
| "LorentzianQ" | whether the metric tensor describes a Lorentzian manifold (i.e. all eigenvalues have the same sign, except for one eigenvalue which has the opposite sign) |
| "RiemannianConditions" | list of conditions required to guarantee that the manifold described by the metric tensor is Riemannian (i.e. all eigenvalues are positive) |
| "PseudoRiemannianConditions" | list of conditions required to guarantee that the manifold described by the metric tensor is pseudo-Riemannian (i.e. all eigenvalues are non-zero) |
| "LorentzianConditions" | list of conditions required to guarantee that the manifold described by the metric tensor is Lorentzian (i.e. the "time" eigenvalue is negative and all other eigenvalues are positive) |
| "MetricSingularities" | list of possible coordinate values that cause the metric tensor to become singular |
| "Determinant" | determinant of the metric tensor (represented in covariant matrix form) |
| "ReducedDeterminant" | determinant of the metric tensor (represented in covariant matrix form), modulo all tensor equivalences |
| "Trace" | trace of the metric tensor |
| "ReducedTrace" | trace of the metric tensor, modulo all tensor equivalences |
| "Eigenvalues" | eigenvalues of the metric tensor (represented in covariant matrix form) |
| "ReducedEigenvalues" | eigenvalues of the metric tensor (represented in covariant matrix form), modulo all tensor equivalences |
| "Eigenvectors" | eigenvectors of the metric tensor (represented in covariant matrix form) |
| "ReducedEigenvectors" | eigenvectors of the metric tensor (represented in covariant matrix form), modulo all tensor equivalences |
| "MetricTensor" | covariant form of the metric tensor (i.e. both indices are lowered/covariant) |
| "InverseMetricTensor" | contravariant form of the metric tensor (i.e. both indices are raised/contravariant) |
| "LineElement" | metric tensor represented as a line element (i.e. an algebraic relationship between "ds" and the differential 1-form symbols for the coordinates) |
| "ReducedLineElement" | metric tensor represented as a line element (i.e. an algebraic relationship between "ds" and the differential 1-form symbols for the coordinates), modulo all tensor equivalences |
| "VolumeForm" | volume form on the manifold (i.e. an algebraic relationship between "dV" and the determinant of the metric tensor) |
| "ReducedVolumeForm" | volume form on the manifold (i.e. an algebraic relationship between "dV" and the determinant of the metric tensor), modulo all tensor equivalences |
| "TimelikeQ" | pure function to determine whether a given tangent vector is timelike (i.e. lies strictly on the interior of a light cone), for a pseudo-Riemannian metric tensor |
| "LightlikeQ" | pure function to determine whether a given tangent vector is lightlike (i.e. lies on the boundary of a light cone), for a pseudo-Riemannian metric tensor |
| "SpacelikeQ" | pure function to determine whether a given tangent vector is spacelike (i.e. lies strictly on the exterior of a light cone), for a pseudo-Riemannian metric tensor |
| "LengthPureFunction" | pure function to determine the length of a given tangent vector, for an arbitrary metric tensor |
| "AnglePureFunction" | pure function to determine the angle between two given tangent vectors, for an arbitrary metric tensor |
| "Properties" | list of properties |
Examples
Basic Examples (4)
Construct a Schwarzschild metric (e.g. for an uncharged, non-rotating black hole with symbolic mass "M") in standard spherical polar coordinates:
| In[1]:= | ![metric = ResourceFunction["MetricTensor"]["Schwarzschild"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2bc3f79c45faa217.png){kind=small} |
| Out[1]= |  |
Show the Schwarzschild metric in explicit matrix form:
| In[2]:= | ![metric["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5169be747154d098.png){kind=small} |
| Out[2]= |  |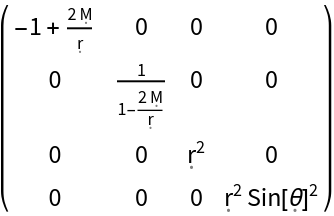
Show the spacetime line element for the Schwarzschild metric:
| In[3]:= | ![metric["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5c69790068d0db6f.png){kind=small} |
| Out[3]= |  |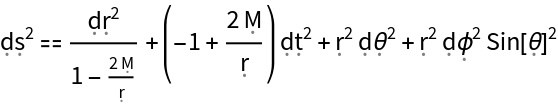
Show the volume form for the Schwarzschild metric:
| In[4]:= | ![metric["VolumeForm"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/167b9b0024cd1ed1.png){kind=small} |
| Out[4]= |  |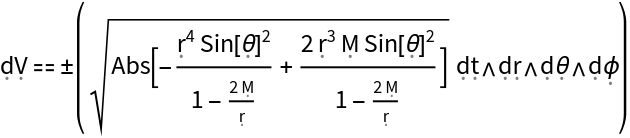
Show the reduced volume form for the Schwarzschild metric, with all algebraic equivalences imposed:
| In[5]:= | ![metric["ReducedVolumeForm"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5093dad18909d5d6.png){kind=small} |
| Out[5]= |  |
Show the list of Schwarzschild coordinate symbols:
| In[6]:= | ![metric["Coordinates"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/70b12c0597831cb3.png){kind=small} |
| Out[6]= |  |
Show the list of differential 1-form symbols for each of the Schwarzschild coordinates:
| In[7]:= | ![metric["CoordinateOneForms"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4c3ee924c6f1c702.png){kind=small} |
| Out[7]= |  |
Show the list of coordinate values that cause the Schwarzschild metric to become singular:
| In[8]:= | ![metric["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2a275ec30d3ef901.png){kind=small} |
| Out[8]= |  |
Show the list of coordinate conditions that must hold for the Schwarzschild metric to be Lorentzian:
| In[9]:= | ![metric["LorentzianConditions"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/729ac4cbf1ee3c95.png){kind=small} |
| Out[9]= |  |
Construct the same (Schwarzschild) metric in spherical polar coordinates, but with numerical mass 1, coordinate symbols t, r, a1 and a2, and both indices raised/contravariant:
| In[10]:= | ![metric2 = ResourceFunction[
"MetricTensor"][{"Schwarzschild", 1}, {t, r, a1, a2}, False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6810f4d20963106d.png){kind=small} |
| Out[10]= |  |
Show the explicit matrix form:
| In[11]:= | ![metric2["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6b7ebafbe17f8a1d.png){kind=small} |
| Out[11]= |  |
Show the reduced explicit matrix form, with all algebraic equivalences imposed:
| In[12]:= | ![metric2["ReducedMatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0143f3d0c5a20878.png){kind=small} |
| Out[12]= |  |
Show the spacetime line element:
| In[13]:= | ![metric2["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/036a37b9d3a678e3.png){kind=small} |
| Out[13]= |  |
Show the reduced spacetime line element, with all algebraic equivalences imposed:
| In[14]:= | ![metric2["ReducedLineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/66f83c6772fd13ba.png){kind=small} |
| Out[14]= |  |
Construct the same (Schwarzschild) metric in isotropic coordinates, in which all light cones appear round:
| In[15]:= | ![metric3 = ResourceFunction["MetricTensor"]["IsotropicSchwarzschild"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2a90fc12ec33cadf.png){kind=small} |
| Out[15]= |  |
| In[16]:= | ![metric3["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/21356770e8615bce.png){kind=small} |
| Out[16]= |  |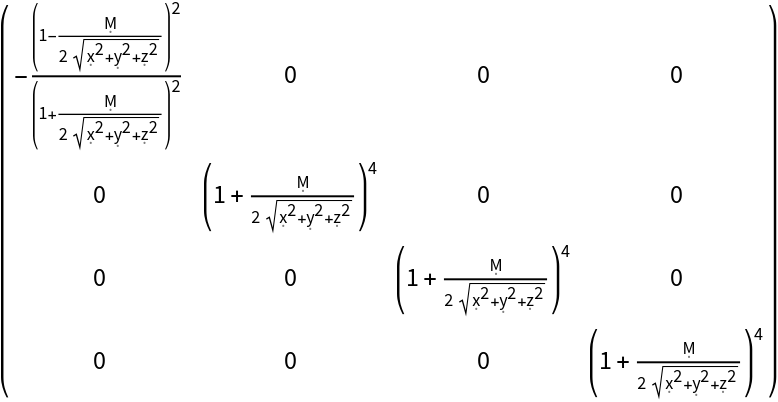
Show the list of metric singularities:
| In[17]:= | ![metric3["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6e77d974b9ff7b84.png){kind=small} |
| Out[17]= |  |
Show that the coordinate singularity at the event horizon disappears when using Eddington-Finkelstein coordinates:
| In[18]:= | ![metric4 = ResourceFunction["MetricTensor"]["EddingtonFinkelstein"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/76be4001a938abab.png){kind=small} |
| Out[18]= |  |
| In[19]:= | ![metric4["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/07ca15374f15badb.png){kind=small} |
| Out[19]= |  |
| In[20]:= | ![metric4["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6507594eadc4e6f0.png){kind=small} |
| Out[20]= |  |
Or Gullstrand-Painlevé coordinates:
| In[21]:= | ![metric5 = ResourceFunction["MetricTensor"]["GullstrandPainleve"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/1ffa5dd70834eb46.png){kind=small} |
| Out[21]= |  |
| In[22]:= | ![metric5["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4714f11b61f3b31b.png){kind=small} |
| Out[22]= |  |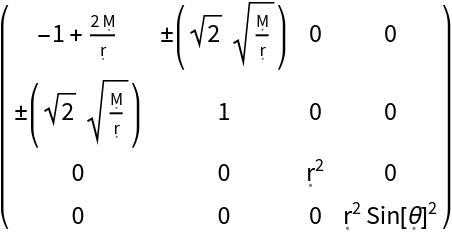
| In[23]:= | ![metric5["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5182b75b1a30509c.png){kind=small} |
| Out[23]= |  |
Construct a Kerr-Newman metric (e.g. for a charged, spinning black hole with symbolic mass "M", symbolic angular momentum "J" and symbolic electric charge "Q") in Boyer-Lindquist/oblate spheroidal coordinates:
| In[24]:= | ![metric = ResourceFunction["MetricTensor"]["KerrNewman"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/75bf57576749f06b.png){kind=small} |
| Out[24]= |  |
| In[25]:= | ![metric["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3309afc5445881c1.png){kind=small} |
| Out[25]= |  |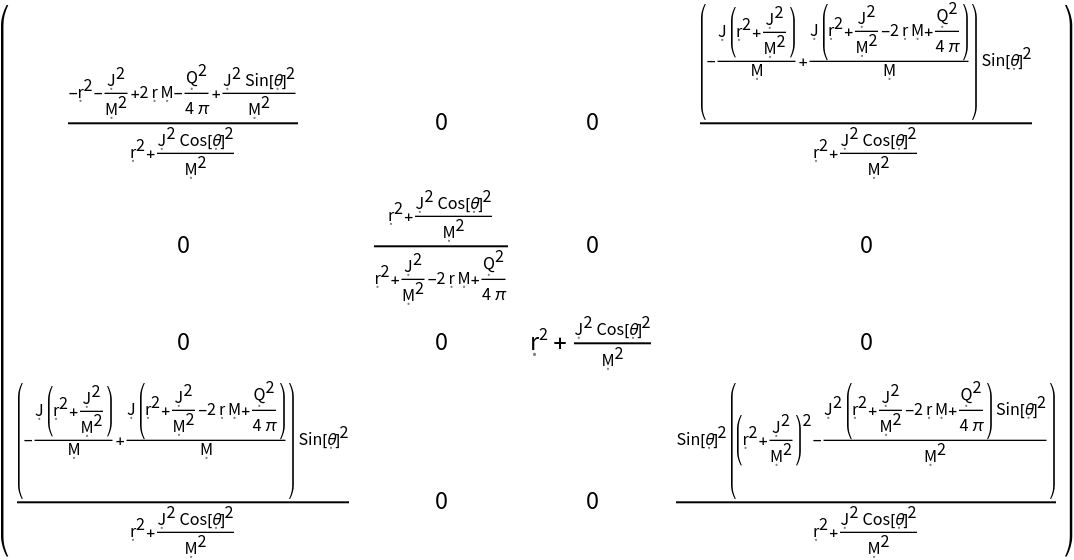
Show the explicit matrix form, with all algebraic equivalences imposed:
| In[26]:= | ![metric["ReducedMatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/70d74ae0e3515959.png){kind=small} |
| Out[26]= |  |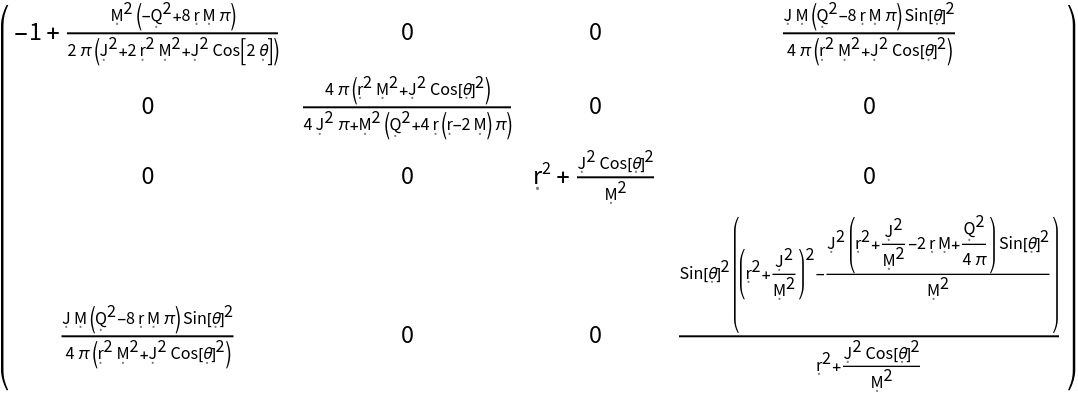
Extract the time-time component of the Kerr-Newman metric:
| In[27]:= | ![metric[1, 1]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/716aa87b026fe6e7.png){kind=small} |
| Out[27]= |  |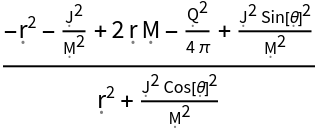
Extract the first row of the Kerr-Newman metric in matrix form:
| In[28]:= | ![metric[1, All]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/35427aa9bf5857ad.png){kind=small} |
| Out[28]= |  |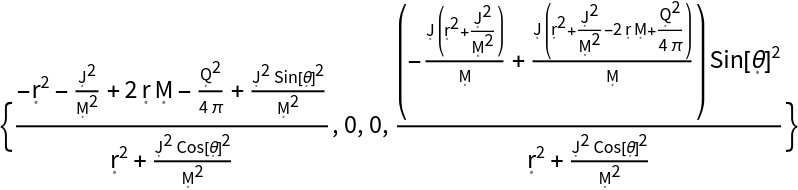
Extract the first column of the Kerr-Newman metric in matrix form:
| In[29]:= | ![metric[All, 1]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5ccf04d7edaa779b.png){kind=small} |
| Out[29]= |  |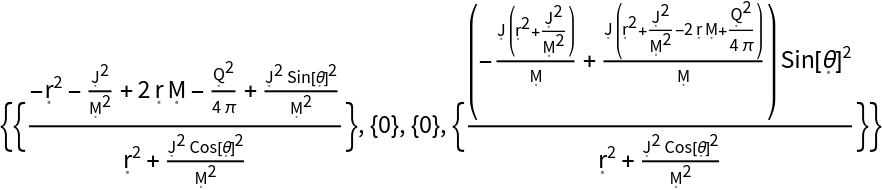
Show the list of metric singularities:
| In[30]:= | ![metric["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2e5b81ee60669ff0.png){kind=small} |
| Out[30]= |  |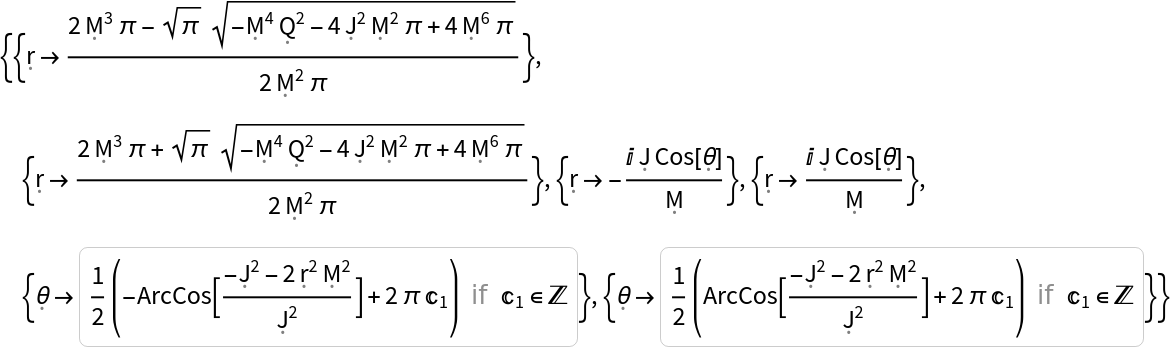
Compute the length of the 4-vector {-1,1,0,0} in the Kerr-Newman geometry:
| In[31]:= | ![metric[{-1, 1, 0, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/29dc5ae8bcf6c06f.png){kind=small} |
| Out[31]= |  |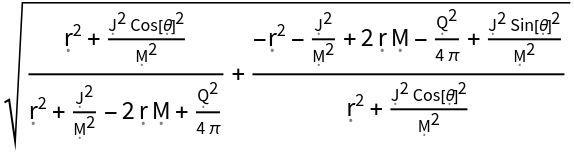
Compute the angle between the 4-vectors {-1,1,0,0} and {-1/2,1/2,1/2,0} in the Kerr-Newman geometry:
| In[32]:= | ![metric[{-1, 1, 0, 0}, {-1/2, 1/2, 1/2, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3249c72097f43707.png){kind=small} |
| Out[32]= |  |
Show the pure function for determining lengths of 4-vectors in the Kerr-Newman geometry:
| In[33]:= | ![metric["LengthPureFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5ae685ad9393c0ab.png){kind=small} |
| Out[33]= |  |
Show the pure function for determining angles between 4-vectors in the Kerr-Newman geometry:
| In[34]:= | ![metric["AnglePureFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/772d64573f86fe0d.png){kind=small} |
| Out[34]= |  |
Applying this pure function directly to the same pair of 4-vectors as above gives the same result:
| In[35]:= | ![metric["AnglePureFunction"][{-1, 1, 0, 0}, {-1/2, 1/2, 1/2, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/36704311dad0f47b.png){kind=small} |
| Out[35]= |  |
Show the pure function for determining whether a 4-vector is timelike (i.e. lies strictly on the interior of a light cone):
| In[36]:= | ![metric["TimelikeQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/16feb85851ef8ea8.png){kind=small} |
| Out[36]= |  |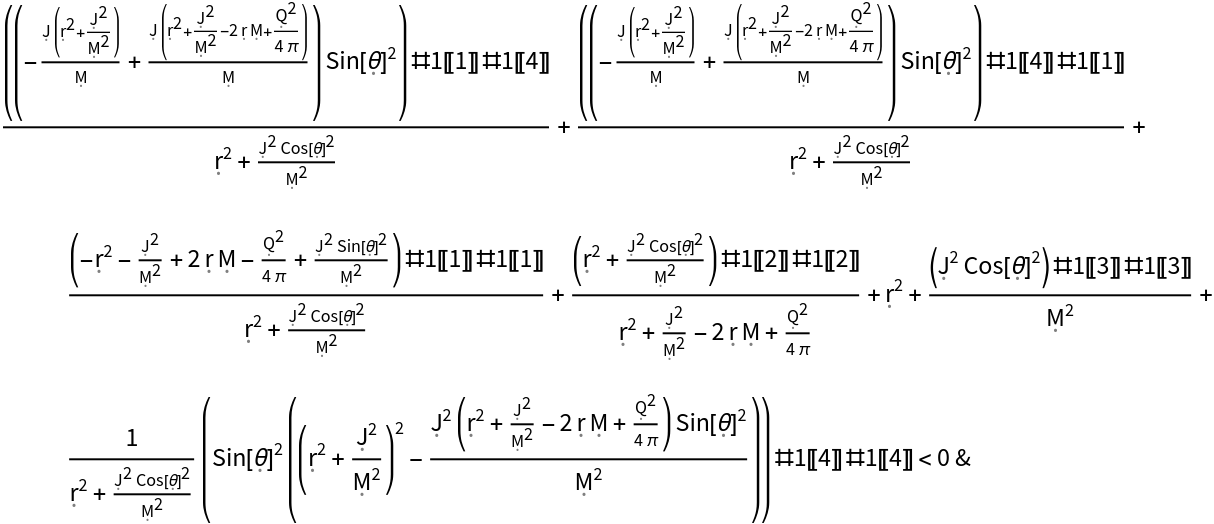
Determine the conditions under which the 4-vector {-1,1,0,0} is spacelike:
| In[37]:= | ![metric["SpacelikeQ"][{-1, 1, 0, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/069d846c322557fe.png){kind=small} |
| Out[37]= |  |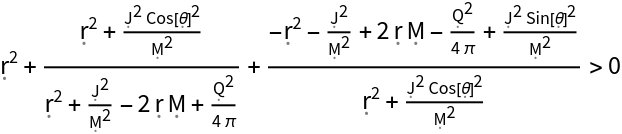
Show that, in the limit as the angular momentum parameter goes to zero, the Kerr-Newman metric becomes equivalent to the Reissner-Nordström metric (e.g. for a charged, non-rotating black hole):
| In[38]:= | ![FullSimplify[
ResourceFunction["MetricTensor"][{"KerrNewman", M, 0, Q}][
"ReducedMatrixRepresentation"] == ResourceFunction["MetricTensor"][{"ReissnerNordstrom", M, Q}][
"ReducedMatrixRepresentation"]]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/50a6127cde11684d.png) |
| Out[38]= |  |
Show that, in the limit as the electric charge parameter goes to zero, the Kerr-Newman metric becomes equivalent to the Kerr metric (e.g. for an uncharged, spinning black hole):
| In[39]:= | ![FullSimplify[
ResourceFunction["MetricTensor"][{"KerrNewman", M, J, 0}][
"ReducedMatrixRepresentation"] == ResourceFunction["MetricTensor"][{"Kerr", M, J}][
"ReducedMatrixRepresentation"]]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/00b5bf18897d174c.png) |
| Out[39]= |  |
Show that, in the limit as the angular momentum and electric charge parameters both go to zero, the Kerr-Newman metric becomes equivalent to the Schwarzschild metric:
| In[40]:= | ![FullSimplify[
ResourceFunction["MetricTensor"][{"KerrNewman", M, 0, 0}][
"ReducedMatrixRepresentation"] == ResourceFunction["MetricTensor"][{"Schwarzschild", M}][
"ReducedMatrixRepresentation"]]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5b76eb4632df0e4c.png) |
| Out[40]= |  |
Construct a metric tensor from a random symmetric matrix:
| In[41]:= | ![randomMatrix = RandomReal[{-1, 1}, {8, 8}];
randomSymmetric = randomMatrix + Transpose[randomMatrix];
randomSymmetric // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/480c5ec3e2f62641.png) |
| Out[43]= |  |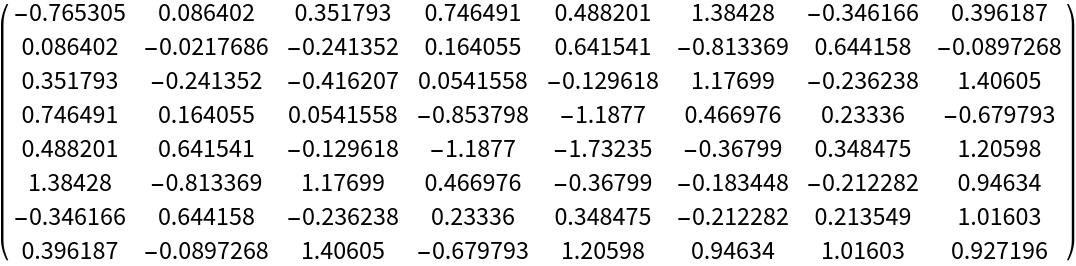
| In[44]:= | ![metric = ResourceFunction["MetricTensor"][randomSymmetric]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/19c9cdae77ad185d.png){kind=small} |
| Out[44]= |  |
Determine whether the metric is Lorentzian:
| In[45]:= | ![metric["LorentzianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4033d76b92f4151c.png){kind=small} |
| Out[45]= |  |
Determine whether the metric is Riemannian:
| In[46]:= | ![metric["RiemannianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/40177eb23fd81011.png){kind=small} |
| Out[46]= |  |
Determine whether the metric is pseudo-Riemannian:
| In[47]:= | ![metric["PseudoRiemannianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/16636a5d0fd6a475.png){kind=small} |
| Out[47]= |  |
Construct a metric tensor for 8-dimensional (i.e. 1+7-dimensional) Minkowski space in Cartesian coordinates:
| In[48]:= | ![metric2 = ResourceFunction["MetricTensor"][{"Minkowski", 8}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/13e9af28a23fd39b.png){kind=small} |
| Out[48]= |  |
| In[49]:= | ![metric2["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2a4730f0bcd79687.png){kind=small} |
| Out[49]= |  |
Show that the Minkowski metric is Lorentzian:
| In[50]:= | ![metric2["LorentzianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4ce3f1f9bddf81f3.png){kind=small} |
| Out[50]= |  |
Construct the most general 5-dimensional (symmetric) metric tensor:
| In[51]:= | ![metric3 = ResourceFunction["MetricTensor"][{"Symmetric", 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0f299a986f6e2dfd.png){kind=small} |
| Out[51]= |  |
| In[52]:= | ![metric3["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/734b655b6f302f03.png){kind=small} |
| Out[52]= |  |
| In[53]:= | ![metric3["SymmetricQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6f0529933b79f2bd.png){kind=small} |
| Out[53]= |  |
Construct the most general 5-dimensional (asymmetric) metric tensor:
| In[54]:= | ![metric4 = ResourceFunction["MetricTensor"][{"Asymmetric", 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/31bdb184a59ffc6e.png){kind=small} |
| Out[54]= |  |
| In[55]:= | ![metric4["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/682e5ac338ed22d2.png){kind=small} |
| Out[55]= |  |
| In[56]:= | ![metric4["SymmetricQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4c7b9487c0f7cf34.png){kind=small} |
| Out[56]= |  |
Construct the most general 5-dimensional (asymmetric) metric tensor field:
| In[57]:= | ![metric5 = ResourceFunction["MetricTensor"][{"AsymmetricField", 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/268a9f433adcb3b3.png){kind=small} |
| Out[57]= |  |
| In[58]:= | ![metric5["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/723eae10359323bb.png){kind=small} |
| Out[58]= |  |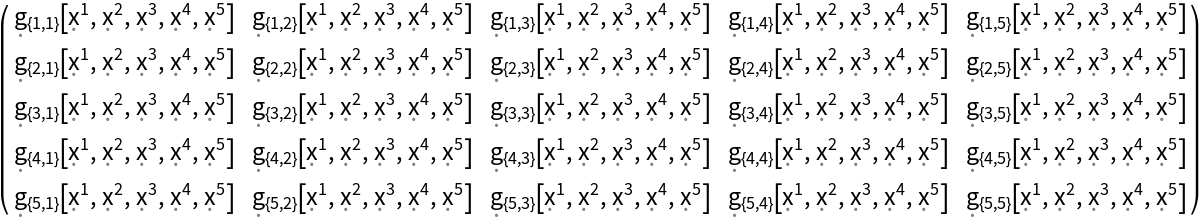
| In[59]:= | ![metric5["SymmetricQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2793ba279d733e41.png){kind=small} |
| Out[59]= |  |
Construct a Friedmann-Lemaître-Robertson-Walker (FLRW) metric for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter "k" and symbolic scale factor "a", in standard spherical polar coordinates:
| In[60]:= | ![metric = ResourceFunction["MetricTensor"]["FLRW"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2b0fc692178f3319.png){kind=small} |
| Out[60]= |  |
| In[61]:= | ![metric["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7d838119353f0a3b.png){kind=small} |
| Out[61]= |  |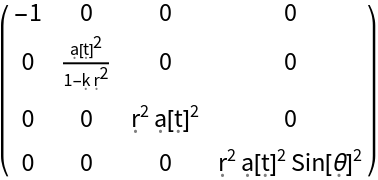
Compute the inverse metric tensor (with both indices raised/contravariant):
| In[62]:= | ![metric2 = metric["InverseMetricTensor"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6eaa39112218176d.png){kind=small} |
| Out[62]= |  |
| In[63]:= | ![metric2["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/210407e79e8f9bb1.png){kind=small} |
| Out[63]= |  |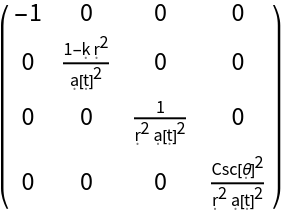
| In[64]:= | ![metric2["ContravariantQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/187669e46bb79f08.png){kind=small} |
| Out[64]= |  |
| In[65]:= | ![metric2["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/175f23de2eb56add.png){kind=small} |
| Out[65]= |  |
Show that having one index raised/contravariant and one index lowered/covariant yields the identity tensor:
| In[66]:= | ![metric3 = ResourceFunction["MetricTensor"][metric, False, True]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/689f399eaee5c76d.png){kind=small} |
| Out[66]= |  |
| In[67]:= | ![metric3["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2fd2bad10f9c90bc.png){kind=small} |
| Out[67]= |  |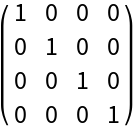
| In[68]:= | ![metric3["MixedQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0d0b61e4f27b6959.png){kind=small} |
| Out[68]= |  |
| In[69]:= | ![metric3["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5b62d5e9a0fc5204.png){kind=small} |
| Out[69]= |  |
Transform to use the new coordinate symbols t, r, a1 and a2:
| In[70]:= | ![metric4 = ResourceFunction["MetricTensor"][metric, {t, r, a1, a2}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5a2afaf8a6783b21.png){kind=small} |
| Out[70]= |  |
| In[71]:= | ![metric4["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2c9466f26c9f817a.png){kind=small} |
| Out[71]= |  |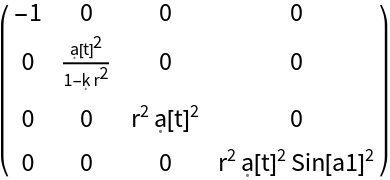
Transform to use the new coordinate symbols t, r, a1 and a2, and raise both indices, simultaneously:
| In[72]:= | ![metric5 = ResourceFunction["MetricTensor"][metric, {t, r, a1, a2}, False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7ffca6d1184265db.png){kind=small} |
| Out[72]= |  |
| In[73]:= | ![metric5["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4bb7040a391f5e77.png){kind=small} |
| Out[73]= |  |
Scope (5)
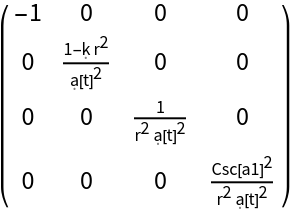Metric tensors can be constructed directly from a matrix representation:
| In[74]:= | ![metric = ResourceFunction["MetricTensor"][DiagonalMatrix[{-1, 1, 1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/69660c5f0d1e680e.png){kind=small} |
| Out[74]= |  |
| In[75]:= | ![metric["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/53f9c595300fe260.png){kind=small} |
| Out[75]= |  |
Additional arguments can be used to specify the coordinate names (otherwise default symbols will be chosen automatically):
| In[76]:= | ![metric2 = ResourceFunction["MetricTensor"][
DiagonalMatrix[{-1, 1, 1, 1}], {t, x, y, z}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3da2c7ce112091f6.png){kind=small} |
| Out[76]= |  |
| In[77]:= | ![metric2["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/19b3c896f71d7b40.png){kind=small} |
| Out[77]= |  |
Or the indices (True for lowered/covariant and False for raised/contravariant - otherwise both indices will be set as lowered/covariant by default):
| In[78]:= | ![metric3 = ResourceFunction["MetricTensor"][DiagonalMatrix[{-1, 1, 1, 1}], False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/26f3996ea14ba258.png){kind=small} |
| Out[78]= |  |
| In[79]:= | ![metric3["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/05eeefced3d32553.png){kind=small} |
| Out[79]= |  |
Or both simultaneously:
| In[80]:= | ![metric3 = ResourceFunction["MetricTensor"][
DiagonalMatrix[{-1, 1, 1, 1}], {t, x, y, z}, True, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/02d795848cbca39c.png){kind=small} |
| Out[80]= |  |
| In[81]:= | ![metric3["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3726b8142ea4b344.png){kind=small} |
| Out[81]= |  |
| In[82]:= | ![metric3["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6cdd24bdae440cf6.png){kind=small} |
| Out[82]= |  |
Common metric tensors can also be constructed using an in-built name:
| In[83]:= | ![metric = ResourceFunction["MetricTensor"]["Godel"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6be4f6880a884f47.png){kind=small} |
| Out[83]= |  |
| In[84]:= | ![metric["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7c5be5172042a2d7.png){kind=small} |
| Out[84]= |  |
When an in-built/named metric has one or more parameters, those parameters can be left unspecified (in which case they are filled with purely symbolic defaults, such as "M"):
| In[85]:= | ![metric2 = ResourceFunction["MetricTensor"]["KerrNewman"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/394bc5961fb9fb10.png){kind=small} |
| Out[85]= |  |
| In[86]:= | ![metric2["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0fa0380c6523332a.png){kind=small} |
| Out[86]= |  |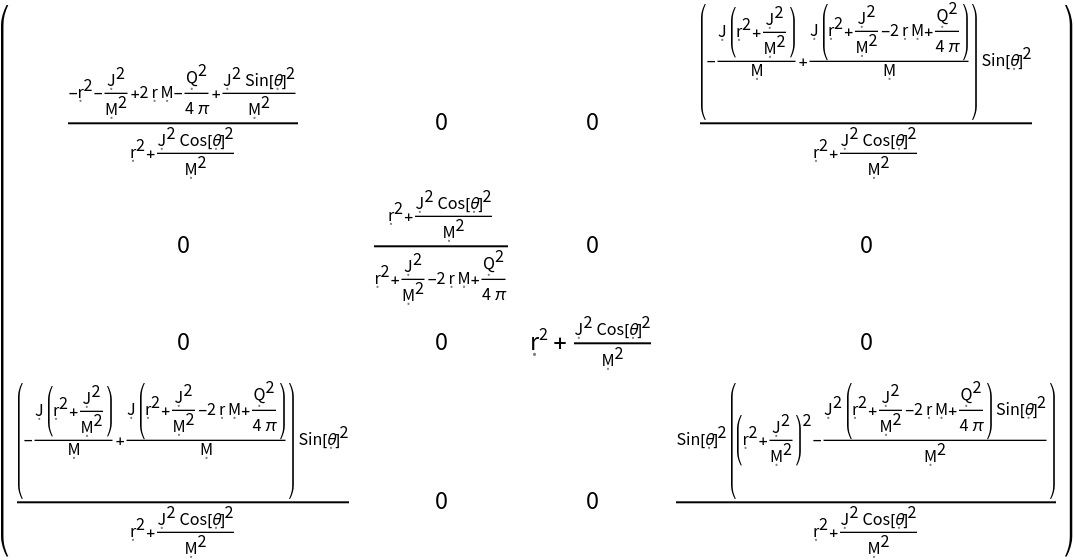
Otherwise, they can be specified explicitly in list form:
| In[87]:= | ![metric3 = ResourceFunction["MetricTensor"][{"KerrNewman", 1, 1/2, 1/3}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/04374915ca7df017.png){kind=small} |
| Out[87]= |  |
| In[88]:= | ![metric3["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/76e56255e70b639a.png){kind=small} |
| Out[88]= |  |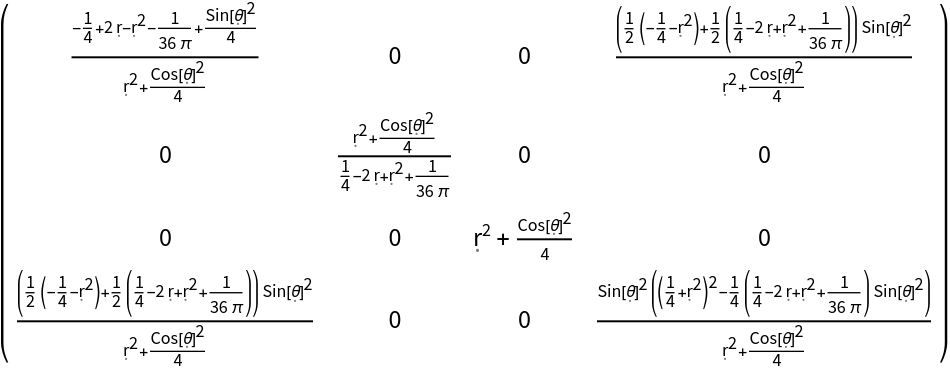
If only some parameters are explicitly specified, then the remainder are filled with symbolic defaults (e.g. if one specifies only a numerical mass and a numerical angular momentum for the Kerr-Newman metric, then MetricTensor will use a purely symbolic electric charge, namely "Q"):
| In[89]:= | ![metric4 = ResourceFunction["MetricTensor"][{"KerrNewman", 1, 1/2}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2316beea581bb6c8.png){kind=small} |
| Out[89]= |  |
| In[90]:= | ![metric4["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/19120f2755edb117.png){kind=small} |
| Out[90]= |  |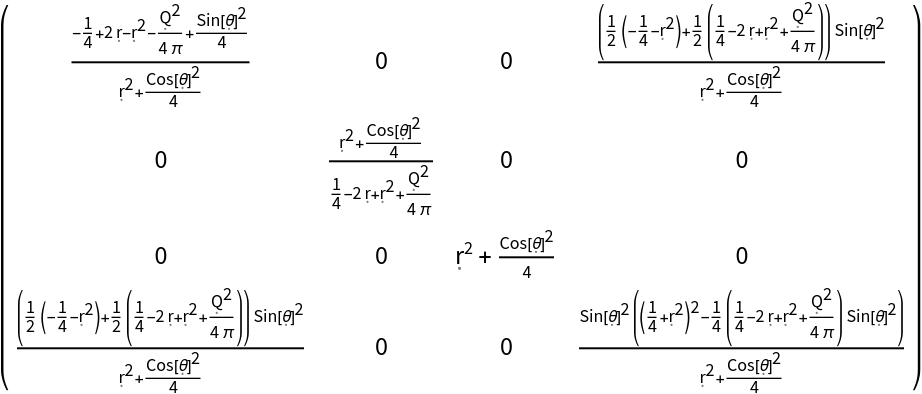
Coordinate and index information can also be specified for in-built/named metrics:
| In[91]:= | ![metric5 = ResourceFunction[
"MetricTensor"][{"KerrNewman", 1, 1/2}, {t, r, a1, a2}, False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0e188687ddb04da4.png){kind=small} |
| Out[91]= |  |
| In[92]:= | ![metric5["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5196f8aeff4bccca.png){kind=small} |
| Out[92]= |  |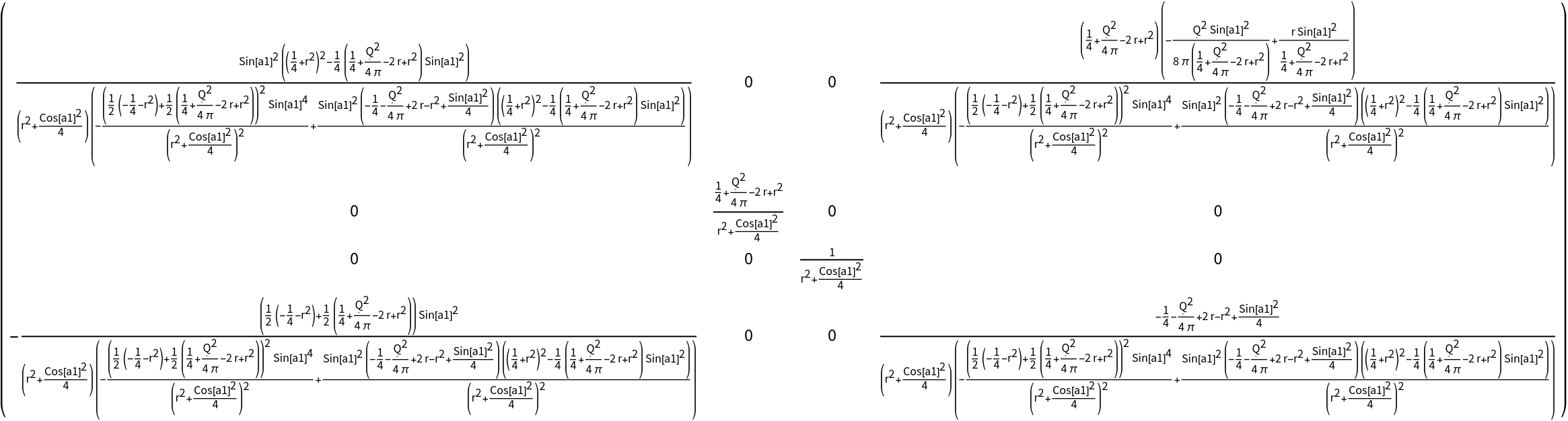
| In[93]:= | ![metric5["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7d622dcb6176c65f.png){kind=small} |
| Out[93]= |  |
New coordinate symbols can be specified for any metric tensor:
| In[94]:= | ![metric = ResourceFunction["MetricTensor"]["IngoingGullstrandPainleve"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3707105c3a8cf314.png){kind=small} |
| Out[94]= |  |
| In[95]:= | ![metric["Coordinates"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5b167394a4afb3c5.png){kind=small} |
| Out[95]= |  |
| In[96]:= | ![metric2 = ResourceFunction["MetricTensor"][metric, {t, r, a1, a2}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5b285a1f525f5912.png){kind=small} |
| Out[96]= |  |
| In[97]:= | ![metric2["Coordinates"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7e6420a0a840a272.png){kind=small} |
| Out[97]= |  |
Indices can also be raised and lowered on any metric tensor:
| In[98]:= | ![metric3 = ResourceFunction["MetricTensor"][metric, False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3695de3cae73abfd.png){kind=small} |
| Out[98]= |  |
| In[99]:= | ![metric3["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7e87369fde3788f8.png){kind=small} |
| Out[99]= |  |
| In[100]:= | ![metric3["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6c2693b75800d747.png){kind=small} |
| Out[100]= |  |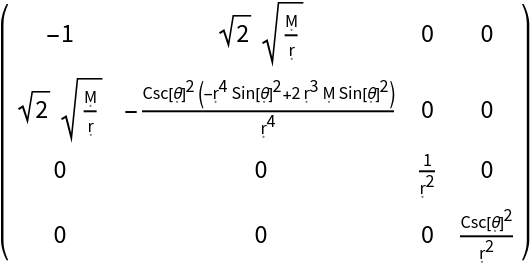
| In[101]:= | ![metric3["ContravariantQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5a6ecb2807c22927.png){kind=small} |
| Out[101]= |  |
New coordinate symbols and new index positions can also be specified simultaneously:
| In[102]:= | ![metric4 = ResourceFunction["MetricTensor"][metric, {t, r, a1, a2}, False, False]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/55aa838f8adad87a.png){kind=small} |
| Out[102]= |  |
| In[103]:= | ![metric4["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/18fe67e86932cac1.png){kind=small} |
| Out[103]= |  |
| In[104]:= | ![metric4["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7e7a0a1e011397b4.png){kind=small} |
| Out[104]= |  |
Show the list of all in-built/named metric tensors:
| In[105]:= | ![ResourceFunction["MetricTensor"][]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4f14590a7b186838.png){kind=small} |
| Out[105]= |  |
Construct a generic 4-dimensional symmetric metric (default):
| In[106]:= | ![ResourceFunction["MetricTensor"]["Symmetric"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/52a6a792029a80ec.png){kind=small} |
| Out[106]= |  |
Construct a generic 5-dimensional symmetric metric:
| In[107]:= | ![ResourceFunction["MetricTensor"][{"Symmetric", 5}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2bc1d533aedaa1ed.png){kind=small} |
| Out[107]= |  |
CallingMetricTensor[d] is a shorthand version, equivalent to calling MetricTensor[{"Symmetric",d}]:
| In[108]:= | ![ResourceFunction["MetricTensor"][5][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/566394a82b8298e6.png){kind=small} |
| Out[108]= |  |
Construct a generic 4-dimensional symmetric metric tensor field (default):
| In[109]:= | ![ResourceFunction["MetricTensor"]["SymmetricField"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/76175fc98d7689ba.png){kind=small} |
| Out[109]= |  |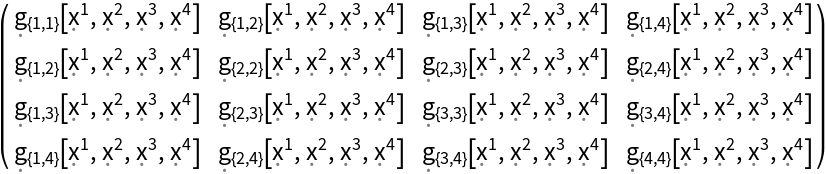
Construct a generic 5-dimensional symmetric metric tensor field:
| In[110]:= | ![ResourceFunction["MetricTensor"][{"SymmetricField", 5}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/76ab7abf15776441.png){kind=small} |
| Out[110]= |  |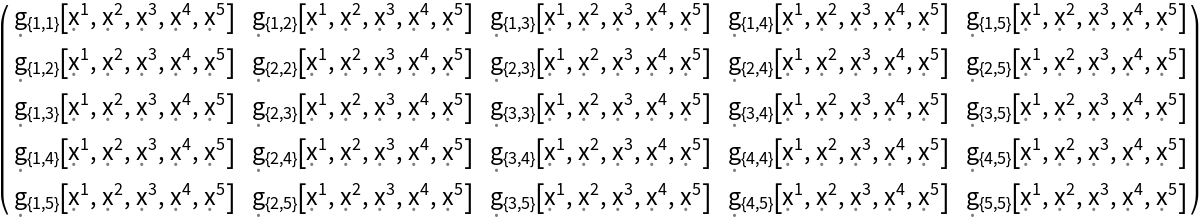
Construct a generic 4-dimensional asymmetric metric (default):
| In[111]:= | ![ResourceFunction["MetricTensor"]["Asymmetric"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/71c5f9be6c93f8d6.png){kind=small} |
| Out[111]= |  |
Construct a generic 5-dimensional asymmetric metric:
| In[112]:= | ![ResourceFunction["MetricTensor"][{"Asymmetric", 5}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2d28f3dc4169a7c1.png){kind=small} |
| Out[112]= |  |
Construct a generic 4-dimensional asymmetric metric tensor field (default):
| In[113]:= | ![ResourceFunction["MetricTensor"]["AsymmetricField"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4ad82fb25c4a43d5.png){kind=small} |
| Out[113]= |  |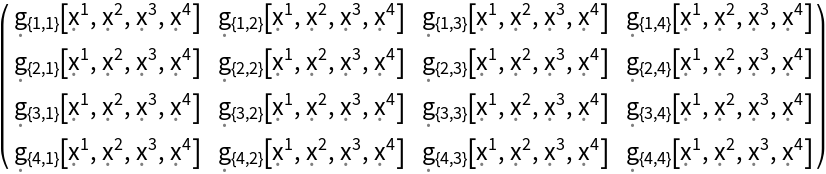
Construct a generic 5-dimensional asymmetric metric tensor field:
| In[114]:= | ![ResourceFunction["MetricTensor"][{"AsymmetricField", 5}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2dea9f7bf337ffec.png){kind=small} |
| Out[114]= |  |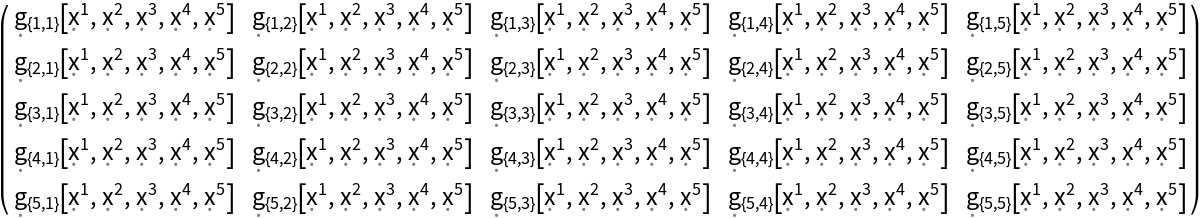
Construct the metric for 3-dimensional flat/Euclidean space (default) in Cartesian coordinates:
| In[115]:= | ![ResourceFunction["MetricTensor"]["Euclidean"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/698ad575f4fc0bc4.png){kind=small} |
| Out[115]= |  |
Construct the metric for 7-dimensional flat/Euclidean space in Cartesian coordinates:
| In[116]:= | ![ResourceFunction["MetricTensor"][{"Euclidean", 7}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7aa28b759173d3db.png){kind=small} |
| Out[116]= |  |
Construct the metric for 4-dimensional (i.e. 1+3-dimensional) Minkowski space (default) in Cartesian coordinates:
| In[117]:= | ![ResourceFunction["MetricTensor"]["Minkowski"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7547dc39b9b19a75.png){kind=small} |
| Out[117]= |  |
Construct the metric for 7-dimensional (i.e. 1+6-dimensional) Minkowski space in Cartesian coordinates:
| In[118]:= | ![ResourceFunction["MetricTensor"][{"Minkowski", 7}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/32b12ab444479378.png){kind=small} |
| Out[118]= |  |
Construct the metric for the Schwarzschild geometry, e.g. the exterior spacetime of an uncharged, non-rotating black hole, with symbolic mass "M" (default) in spherical polar coordinates:
| In[119]:= | ![ResourceFunction["MetricTensor"]["Schwarzschild"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/216450f5e2724492.png){kind=small} |
| Out[119]= |  |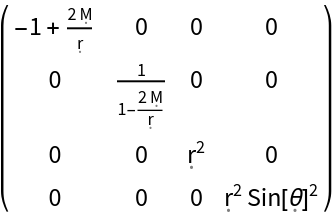
Construct the metric for the Schwarzschild geometry with numerical mass 1 in spherical polar coordinates:
| In[120]:= | ![ResourceFunction["MetricTensor"][{"Schwarzschild", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6bf23a8fbbd8755e.png){kind=small} |
| Out[120]= |  |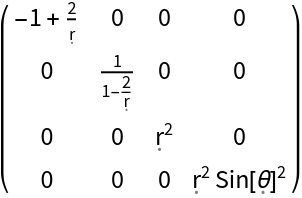
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in Cartesian-like/isotropic coordinates, in which all light cones appear round:
| In[121]:= | ![ResourceFunction["MetricTensor"]["IsotropicSchwarzschild"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/641364fcfdfafc89.png){kind=small} |
| Out[121]= |  |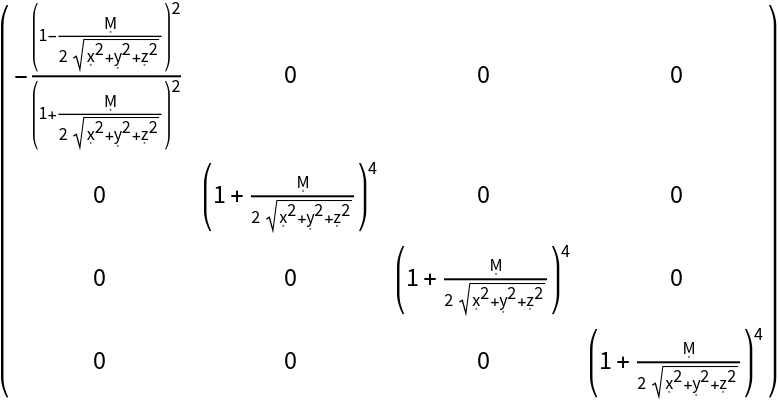
Construct the metric for the Schwarzschild geometry with numerical mass 1 in Cartesian-like/isotropic coordinates:
| In[122]:= | ![ResourceFunction["MetricTensor"][{"IsotropicSchwarzschild", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2892e87b2a8ada0b.png){kind=small} |
| Out[122]= |  |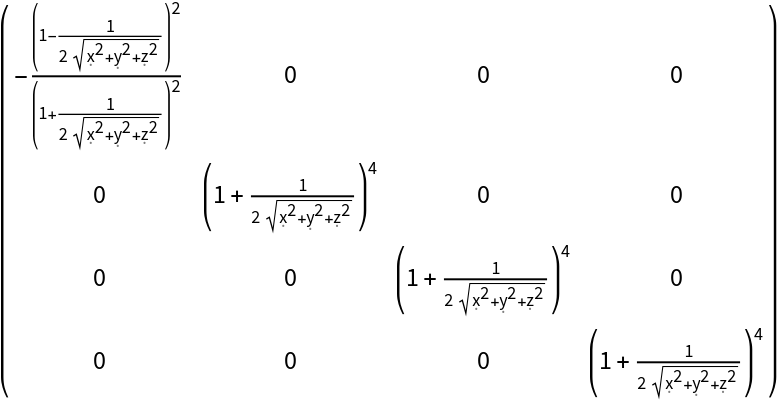
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in Eddington-Finkelstein coordinates, adapted to radial lightlike geodesics:
| In[123]:= | ![ResourceFunction["MetricTensor"]["EddingtonFinkelstein"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/148ff024f944553c.png){kind=small} |
| Out[123]= |  |
Construct the metric for the Schwarzschild geometry with numerical mass 1 in Eddington-Finkelstein coordinates:
| In[124]:= | ![ResourceFunction["MetricTensor"][{"EddingtonFinkelstein", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5a60b8c78dcf792e.png){kind=small} |
| Out[124]= |  |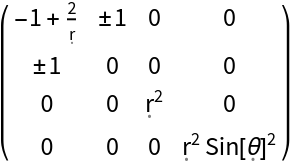
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in ingoing Eddington-Finkelstein coordinates, adapted to inward-traveling radial lightlike geodesics:
| In[125]:= | ![ResourceFunction["MetricTensor"]["IngoingEddingtonFinkelstein"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/27dfdc04223b1177.png){kind=small} |
| Out[125]= |  |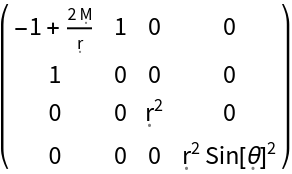
Construct the metric for the Schwarzschild geometry with numerical mass 1 in ingoing Eddington-Finkelstein coordinates:
| In[126]:= | ![ResourceFunction["MetricTensor"][{"IngoingEddingtonFinkelstein", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/36228021ef8a8d6d.png){kind=small} |
| Out[126]= |  |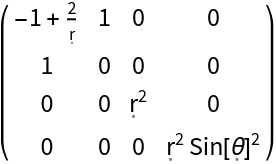
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in outgoing Eddington-Finkelstein coordinates, adapted to outward-traveling radial lightlike geodesics:
| In[127]:= | ![ResourceFunction["MetricTensor"]["OutgoingEddingtonFinkelstein"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2cbfb3080ede7513.png){kind=small} |
| Out[127]= |  |
Construct the metric for the Schwarzschild geometry with numerical mass 1 in outgoing Eddington-Finkelstein coordinates:
| In[128]:= | ![ResourceFunction["MetricTensor"][{"OutgoingEddingtonFinkelstein", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2fcaf4eeec4b8645.png){kind=small} |
| Out[128]= |  |
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in Gullstrand-Painlevé coordinates, in which coordinate time is the proper time experienced by a free-falling observer from infinity:
| In[129]:= | ![ResourceFunction["MetricTensor"]["GullstrandPainleve"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/061d59956b98ce62.png){kind=small} |
| Out[129]= |  |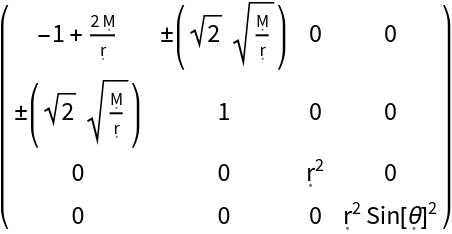
Construct the metric for the Schwarzschild geometry with numerical mass 1 in Gullstrand-Painlevé coordinates:
| In[130]:= | ![ResourceFunction["MetricTensor"][{"GullstrandPainleve", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0cd3324013103e9d.png){kind=small} |
| Out[130]= |  |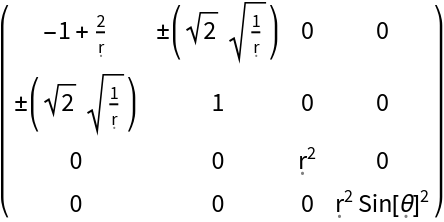
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in ingoing Gullstrand-Painlevé coordinates, in which coordinate time is the proper time experienced by a free-falling observer, falling inwards from infinity:
| In[131]:= | ![ResourceFunction["MetricTensor"]["IngoingGullstrandPainleve"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2418f1434ced173c.png){kind=small} |
| Out[131]= |  |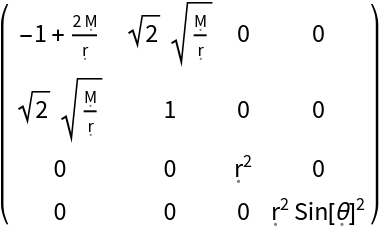
Construct the metric for the Schwarzschild geometry with numerical mass 1 in ingoing Gullstrand-Painlevé coordinates:
| In[132]:= | ![ResourceFunction["MetricTensor"][{"IngoingGullstrandPainleve", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/13119f0c3b57979d.png){kind=small} |
| Out[132]= |  |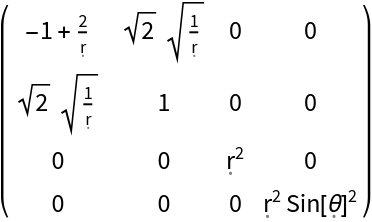
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in outgoing Gullstrand-Painlevé coordinates, in which coordinate time is the proper time experienced by a free-falling observer, falling outwards to infinity:
| In[133]:= | ![ResourceFunction["MetricTensor"]["OutgoingGullstrandPainleve"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/38a515e2e6d9d683.png){kind=small} |
| Out[133]= |  |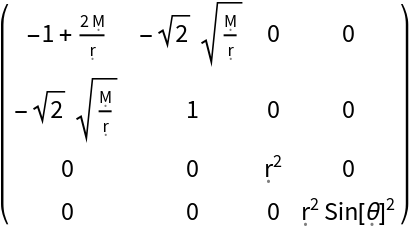
Construct the metric for the Schwarzschild geometry with numerical mass 1 in outgoing Gullstrand-Painlevé coordinates:
| In[134]:= | ![ResourceFunction["MetricTensor"][{"OutgoingGullstrandPainleve", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/39a3329f49335d78.png){kind=small} |
| Out[134]= |  |
Construct the metric for the Schwarzschild geometry with symbolic mass "M" (default) in Kruskal-Szekeres coordinates, which cover the complete spacetime manifold for the maximal analytic extension of the Schwarzschild metric:
| In[135]:= | ![ResourceFunction["MetricTensor"]["KruskalSzekeres"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0023b65edd8d09d4.png){kind=small} |
| Out[135]= |  |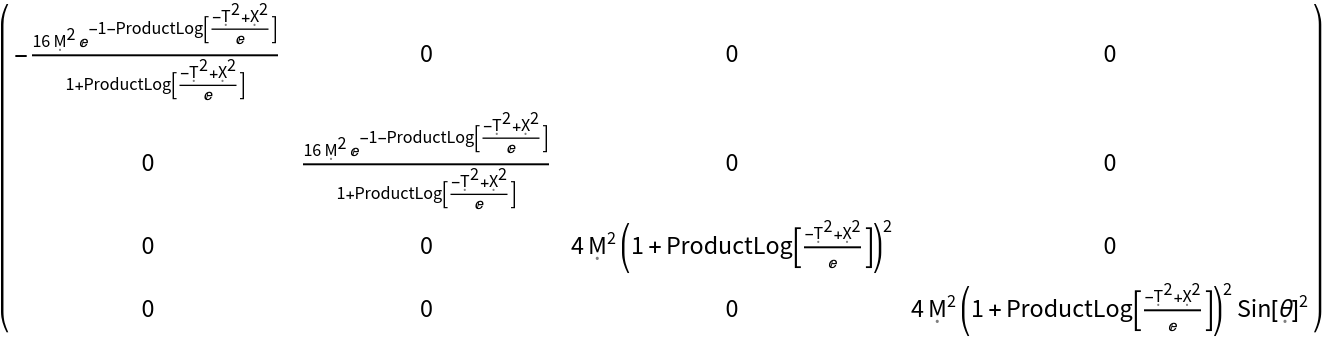
Construct the metric for the Schwarzschild geometry with numerical mass 1 in Kruskal-Szekeres coordinates:
| In[136]:= | ![ResourceFunction["MetricTensor"][{"KruskalSzekeres", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2758459cea433911.png){kind=small} |
| Out[136]= |  |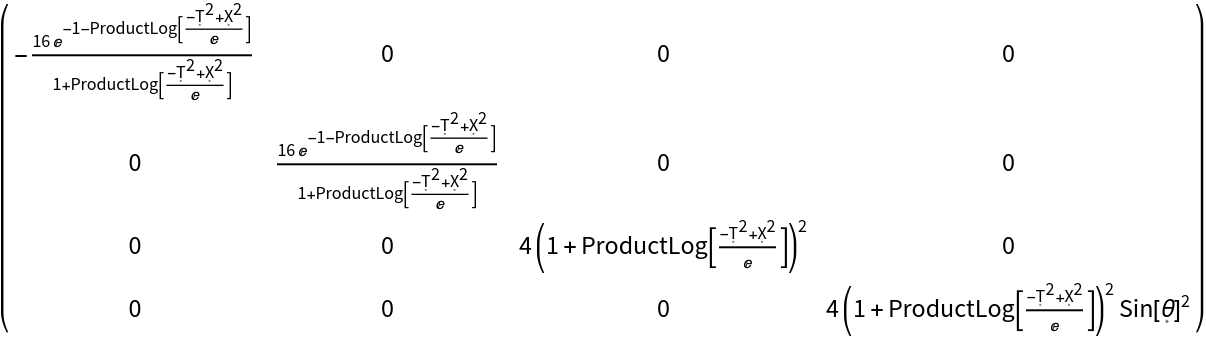
Construct the metric for the Kerr geometry, e.g. the exterior spacetime of an uncharged, spinning black hole, with symbolic mass "M" and symbolic angular momentum "J" (default) in Boyer-Lindquist/oblate spheroidal coordinates:
| In[137]:= | ![ResourceFunction["MetricTensor"]["Kerr"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6d9b4af2f8a8c25f.png){kind=small} |
| Out[137]= |  |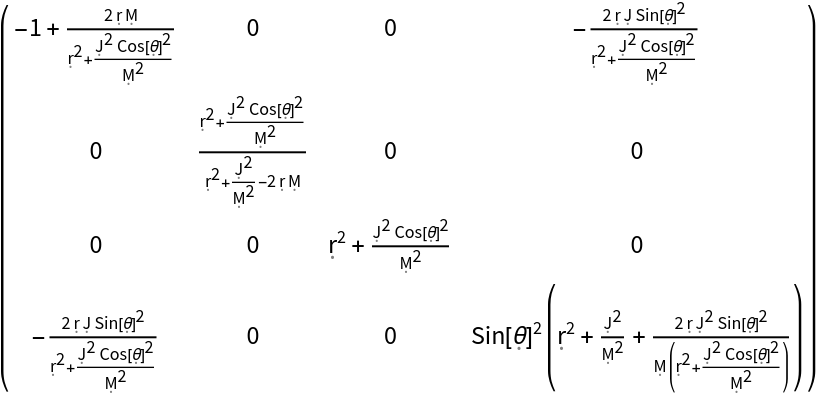
Construct the metric for the Kerr geometry with numerical mass 1 and symbolic angular momentum "J" in Boyer-Lindquist/oblate spheroidal coordinates:
| In[138]:= | ![ResourceFunction["MetricTensor"][{"Kerr", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/15ad1f7b14b5d281.png){kind=small} |
| Out[138]= |  |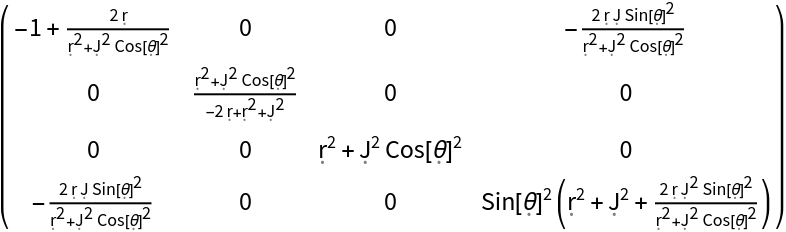
Construct the metric for the Kerr geometry with numerical mass 1 and numerical angular momentum 1/2 in Boyer-Lindquist/oblate spheroidal coordinates:
| In[139]:= | ![ResourceFunction["MetricTensor"][{"Kerr", 1, 1/2}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/23ff66585c436e06.png){kind=small} |
| Out[139]= |  |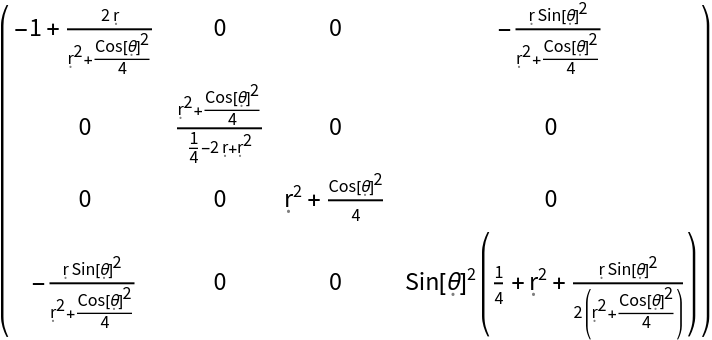
Construct the metric for the Reissner-Nordström geometry, e.g. the exterior spacetime of a charged, non-rotating black hole, with symbolic mass "M" and symbolic electric charge "Q" (default) in spherical polar coordinates:
| In[140]:= | ![ResourceFunction["MetricTensor"]["ReissnerNordstrom"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/62cae1e1a5711cce.png){kind=small} |
| Out[140]= |  |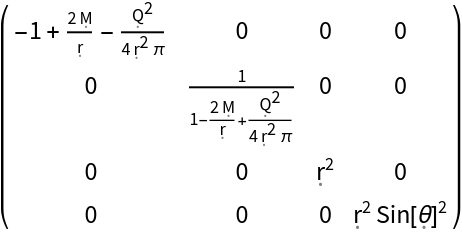
Construct the metric for the Reissner-Nordström geometry with numerical mass 1 and symbolic electric charge "Q" in spherical polar coordinates:
| In[141]:= | ![ResourceFunction["MetricTensor"][{"ReissnerNordstrom", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/1215aef73f0b24b3.png){kind=small} |
| Out[141]= |  |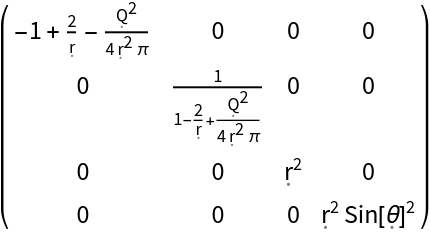
Construct the metric for the Reissner-Nordström geometry with numerical mass 1 and numerical electric charge 1/3 in spherical polar coordinates:
| In[142]:= | ![ResourceFunction["MetricTensor"][{"ReissnerNordstrom", 1, 1/3}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6709c9abd4b67501.png){kind=small} |
| Out[142]= |  |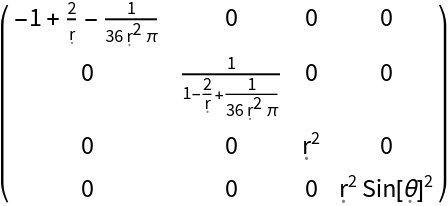
Construct the metric for the Kerr-Newman geometry, e.g. the exterior spacetime of a charged, spinning black hole, with symbolic mass "M", symbolic angular momentum "J" and symbolic electric charge "Q" (default) in Boyer-Lindquist/oblate spheroidal coordinates:
| In[143]:= | ![ResourceFunction["MetricTensor"]["KerrNewman"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5ff636b9e47bfe12.png){kind=small} |
| Out[143]= |  |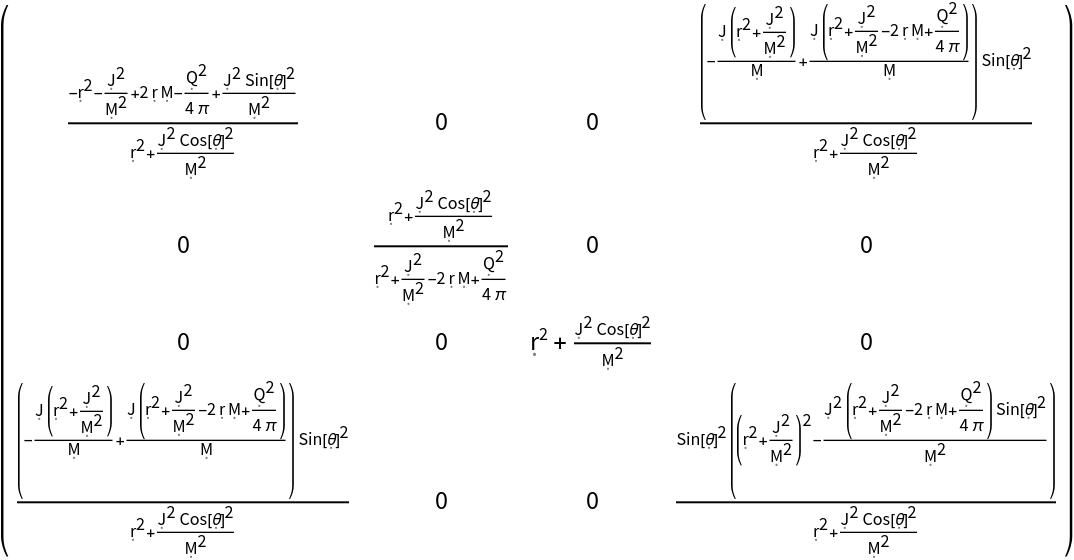
Construct the metric for the Kerr-Newman geometry with numerical mass 1, symbolic angular momentum "J" and symbolic electric charge "Q" in Boyer-Lindquist/oblate spheroidal coordinates:
| In[144]:= | ![ResourceFunction["MetricTensor"][{"KerrNewman", 1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/1197f75a946e2a64.png){kind=small} |
| Out[144]= |  |
Construct the metric for the Kerr-Newman geometry with numerical mass 1, numerical angular momentum 1/2 and symbolic electric charge "Q" in Boyer-Lindquist/oblate spheroidal coordinates:
| In[145]:= | ![ResourceFunction["MetricTensor"][{"KerrNewman", 1, 1/2}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0f7e7830ddb2c1c6.png){kind=small} |
| Out[145]= |  |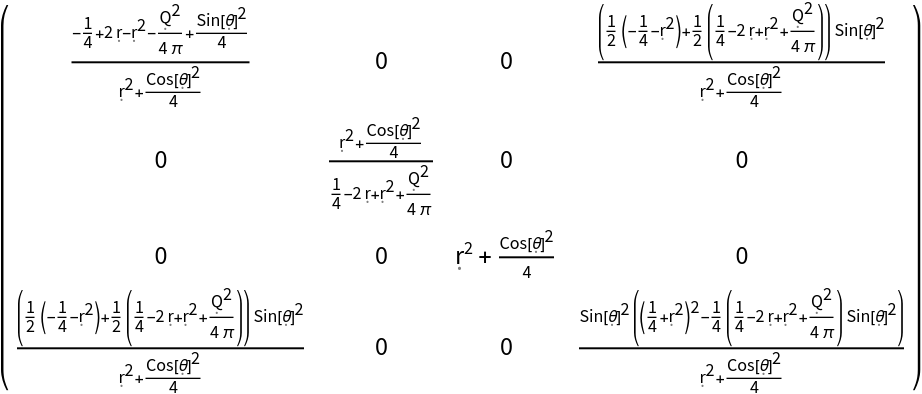
Construct the metric for the Kerr-Newman geometry with numerical mass 1, numerical angular momentum 1/2 and numerical electric charge 1/3 in Boyer-Lindquist/oblate spheroidal coordinates:
| In[146]:= | ![ResourceFunction["MetricTensor"][{"KerrNewman", 1, 1/2, 1/3}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3f7b95b5c1348835.png){kind=small} |
| Out[146]= |  |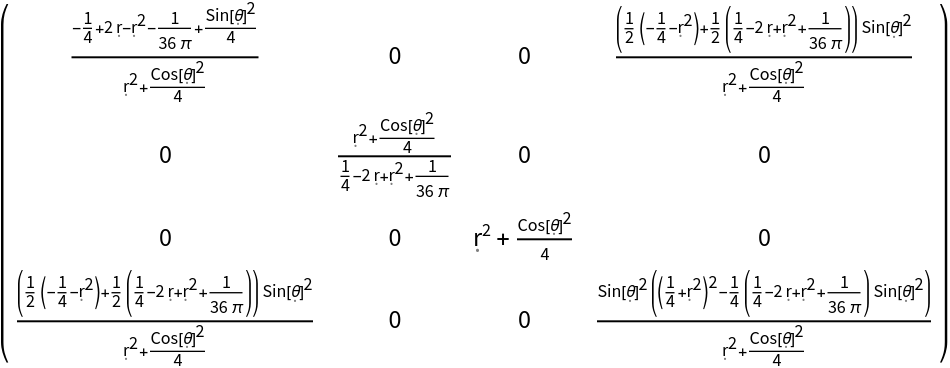
Construct the Gödel metric, i.e. the metric for a rotating, dust-filled universe, with symbolic angular velocity "" (default) in Gödel's Cartesian-like coordinates:
| In[147]:= | ![ResourceFunction["MetricTensor"]["Godel"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5c047900e8ae02da.png){kind=small} |
| Out[147]= |  |
Construct the Gödel metric with numerical angular velocity 1/2 in Gödel's Cartesian-like coordinates:
| In[148]:= | ![ResourceFunction["MetricTensor"][{"Godel", 1/2}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3ea5692d3132c065.png){kind=small} |
| Out[148]= |  |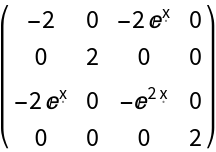
Construct the Friedmann-Lemaître-Robertson-Walker/FLRW metric, i.e. the metric for a homogeneous, isotropic and uniformly expanding/contracting universe, with symbolic global curvature "k" and symbolic scale function "a" (default) in spherical polar coordinates:
| In[149]:= | ![ResourceFunction["MetricTensor"]["FLRW"][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/399038ab0f1bcda7.png){kind=small} |
| Out[149]= |  |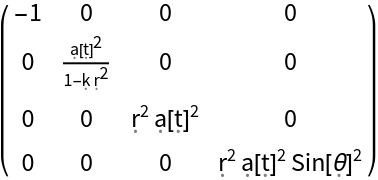
Construct the FLRW metric with numerical global curvature -1 and symbolic scale function "a" in spherical polar coordinates:
| In[150]:= | ![ResourceFunction["MetricTensor"][{"FLRW", -1}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/66c99ee944c07042.png){kind=small} |
| Out[150]= |  |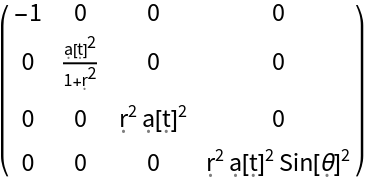
Construct the FLRW metric with numerical global curvature -1 and numerical scale function (#*3)& in spherical polar coordinates:
| In[151]:= | ![ResourceFunction["MetricTensor"][{"FLRW", -1, (#*3) &}][
"MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/77bb4a0d99c87dbe.png){kind=small} |
| Out[151]= |  |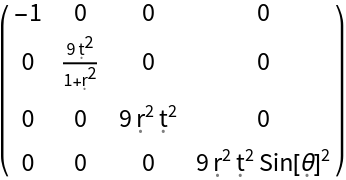
Construct a Schwarzschild metric, with symbolic mass "M":
| In[152]:= | ![metric = ResourceFunction["MetricTensor"]["Schwarzschild"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/083d19672873d16e.png){kind=small} |
| Out[152]= |  |
Show the list of properties:
| In[153]:= | ![metric["Properties"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/09903ad100c7ba24.png){kind=small} |
| Out[153]= |  |
Show the explicit matrix representation of the metric tensor:
| In[154]:= | ![metric["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3a623ee6ccf2be0e.png){kind=small} |
| Out[154]= |  |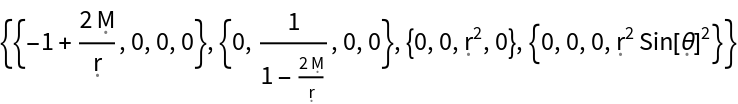
Show the explicit matrix representation of the metric tensor, with all algebraic equivalences imposed:
| In[155]:= | ![metric["ReducedMatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3d950ff34e0e5f23.png){kind=small} |
| Out[155]= |  |
Show the list of coordinate symbols for the metric tensor:
| In[156]:= | ![metric["Coordinates"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/59865d302e94ecc5.png){kind=small} |
| Out[156]= |  |
Show the list of differential 1-form symbols for the coordinates of the metric tensor:
| In[157]:= | ![metric["CoordinateOneForms"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3327ee049fd1552c.png){kind=small} |
| Out[157]= |  |
Show the list of booleans specifying the positions of the indices of the metric tensor (True for lowered/covariant and False for raised/contravariant):
| In[158]:= | ![metric["Indices"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/29e1468e3a778111.png){kind=small} |
| Out[158]= |  |
Determine whether the metric tensor is covariant (i.e. both indices are lowered/covariant):
| In[159]:= | ![metric["CovariantQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4c12c2a91a9cd759.png){kind=small} |
| Out[159]= |  |
Determine whether the metric tensor is contravariant (i.e. both indices are raised/contravariant):
| In[160]:= | ![metric["ContravariantQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/677c324aeb035964.png){kind=small} |
| Out[160]= |  |
Determine whether the metric tensor is mixed (i.e. one index is lowered/covariant and one index is raised/contravariant):
| In[161]:= | ![metric["MixedQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/7a9ad4073eb468b5.png){kind=small} |
| Out[161]= |  |
Show a symbolic representation of the metric tensor with appropriately raised/lowered indices:
| In[162]:= | ![metric["Symbol"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/19b24d80b139c816.png){kind=small} |
| Out[162]= |  |
Show the number of dimensions of the underlying manifold represented by the metric tensor:
| In[163]:= | ![metric["Dimensions"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/285decef11c257e5.png){kind=small} |
| Out[163]= |  |
Determine whether the metric tensor is symmetric (in explicit, covariant matrix form):
| In[164]:= | ![metric["SymmetricQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/41df47d468a56395.png){kind=small} |
| Out[164]= |  |
Determine whether the metric tensor is diagonal (in explicit, covariant matrix form):
| In[165]:= | ![metric["DiagonalQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3099f1e65aa8165b.png){kind=small} |
| Out[165]= |  |
Show the signature of the metric tensor (with +1s representing positive eigenvalues and -1s representing negative eigenvalues):
| In[166]:= | ![metric["Signature"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2178944d3e5e91ec.png){kind=small} |
| Out[166]= |  |
Determine whether the metric tensor is Riemannian (i.e. all eigenvalues have the same sign):
| In[167]:= | ![metric["RiemannianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2feb59879bc538c3.png){kind=small} |
| Out[167]= |  |
Determine whether the metric tensor is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):
| In[168]:= | ![metric["PseudoRiemannianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/372930bf7bec697c.png){kind=small} |
| Out[168]= |  |
Determine whether the metric tensor is Lorentzian (i.e. all eigenvalues have the same sign, except for one eigenvalue which has the opposite sign):
| In[169]:= | ![metric["LorentzianQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2c4bfb5a3a1f1157.png){kind=small} |
| Out[169]= |  |
Show the list of conditions on the coordinates required to guarantee that the metric tensor is Riemannian (i.e. all eigenvalues are positive):
| In[170]:= | ![metric["RiemannianConditions"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/48642ab5d160486a.png){kind=small} |
| Out[170]= |  |
Show the list of conditions on the coordinates required to guarantee that the metric tensor is pseudo-Riemannian (i.e. all eigenvalues are non-zero):
| In[171]:= | ![metric["PseudoRiemannianConditions"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/1c35996e9d1f689a.png){kind=small} |
| Out[171]= |  |
Show the list of conditions on the coordinates required to guarantee that the metric tensor is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):
| In[172]:= | ![metric["LorentzianConditions"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/44c26d8eb7ecbb44.png){kind=small} |
| Out[172]= |  |
Show the list of coordinate values that cause the metric tensor to become singular:
| In[173]:= | ![metric["MetricSingularities"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/146c4d7792bfd81c.png){kind=small} |
| Out[173]= |  |
Show the determinant of the metric tensor (when represented as a covariant matrix):
| In[174]:= | ![metric["Determinant"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/01606691aa9b27db.png){kind=small} |
| Out[174]= |  |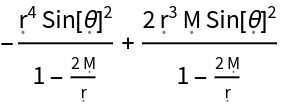
Show the determinant of the metric tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
| In[175]:= | ![metric["ReducedDeterminant"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/537a5f974038f31c.png){kind=small} |
| Out[175]= |  |
Show the trace of the metric tensor:
| In[176]:= | ![metric["Trace"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/25cdd96c95f4aa06.png){kind=small} |
| Out[176]= |  |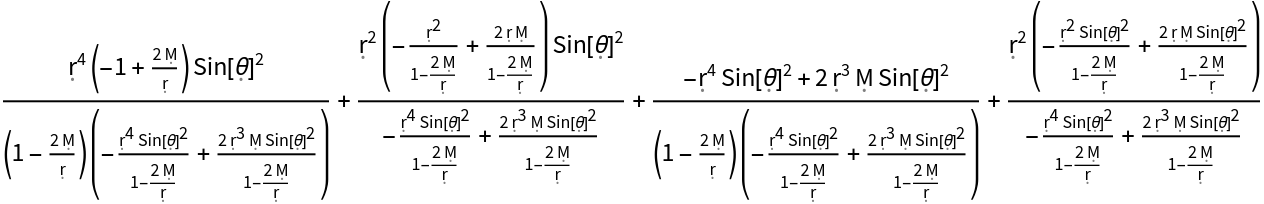
Show the trace of the metric tensor, with all algebraic equivalences imposed:
| In[177]:= | ![metric["ReducedTrace"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/74282999a4a9b93c.png){kind=small} |
| Out[177]= |  |
Show the eigenvalues of the metric tensor (when represented as a covariant matrix):
| In[178]:= | ![metric["Eigenvalues"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/243f3f5d40635e8c.png){kind=small} |
| Out[178]= |  |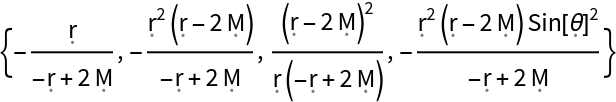
Show the eigenvalues of the metric tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
| In[179]:= | ![metric["ReducedEigenvalues"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/4078ba97498f0589.png){kind=small} |
| Out[179]= |  |
Show the eigenvectors of the metric tensor (when represented as a covariant matrix):
| In[180]:= | ![metric["Eigenvectors"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/338076edd6ae5903.png){kind=small} |
| Out[180]= |  |
Show the eigenvectors of the metric tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
| In[181]:= | ![metric["ReducedEigenvectors"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/5c1e0a8b43a497de.png){kind=small} |
| Out[181]= |  |
Compute the covariant form of the metric tensor (with both indices lowered/covariant):
| In[182]:= | ![metric["MetricTensor"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/53cb2e4fbd350aa0.png){kind=small} |
| Out[182]= |  |
Compute the contravariant form of the metric tensor (with both indices raised/contravariant), otherwise known as the inverse metric tensor:
| In[183]:= | ![metric["InverseMetricTensor"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/0ea97106190d855a.png){kind=small} |
| Out[183]= |  |
Show the spacetime line element for the metric tensor (i.e. the algebraic relationship between "ds" and the differential 1-form symbols for the coordinates):
| In[184]:= | ![metric["LineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/1b9a86e9cb99ba3e.png){kind=small} |
| Out[184]= |  |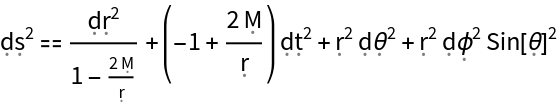
Show the spacetime line element for the metric tensor (i.e. the algebraic relationship between "ds" and the differential 1-form symbols for the coordinates), with all algebraic equivalences imposed:
| In[185]:= | ![metric["ReducedLineElement"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/30cbcd02c4763a1d.png){kind=small} |
| Out[185]= |  |
Show the volume form (i.e. the algebraic relationship between "dV" and the determinant of the metric tensor):
| In[186]:= | ![metric["VolumeForm"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6ed37c7f23fc5079.png){kind=small} |
| Out[186]= |  |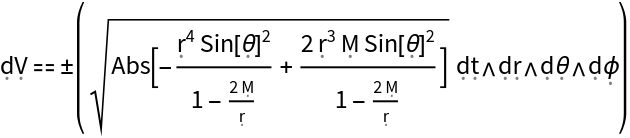
Show the volume form (i.e. the algebraic relationship between "dV" and the determinant of the metric tensor), with all algebraic equivalences imposed:
| In[187]:= | ![metric["ReducedVolumeForm"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6f7ead538b0e77b5.png){kind=small} |
| Out[187]= |  |
Show the pure function for determining whether tangent vectors are timelike (i.e. whether they lie strictly on the interiors of light cones) for a pseudo-Riemannian metric tensor:
| In[188]:= | ![metric["TimelikeQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/6c930c556cfd26c1.png){kind=small} |
| Out[188]= |  |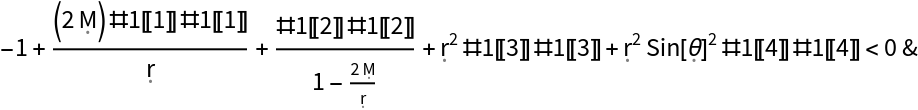
Show the pure function for determining whether tangent vectors are lightlike (i.e. whether they lie on the boundaries of light cones) for a pseudo-Riemannian metric tensor:
| In[189]:= | ![metric["LightlikeQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/3e61d3bbb9929238.png){kind=small} |
| Out[189]= |  |
Show the pure function for determining whether tangent vectors are spacelike (i.e. whether they lie strictly on the exteriors of light cones) for a pseudo-Riemannian metric tensor:
| In[190]:= | ![metric["SpacelikeQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/22bf80b6c9bf4897.png){kind=small} |
| Out[190]= |  |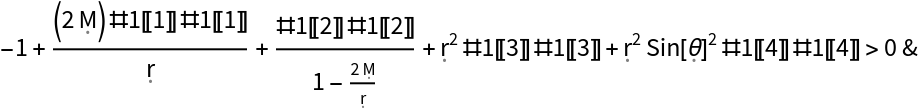
Show the pure function for determining the lengths of tangent vectors for an arbitrary metric tensor:
| In[191]:= | ![metric["LengthPureFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/2eaf67a9d2a35ca1.png){kind=small} |
| Out[191]= |  |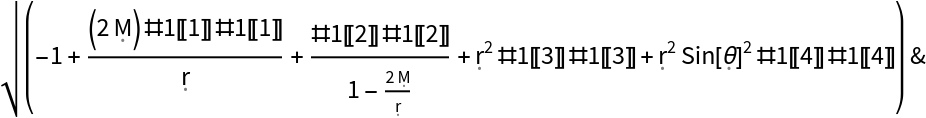
Show the pure function for determining the angles between pairs of tangent vectors for an arbitrary metric tensor:
| In[192]:= | ![metric["AnglePureFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/c6c/c6c98873-a3bc-43e4-a1a4-ed6e5dbbaa32/298c004cb4b1e6e0.png){kind=small} |
| Out[192]= |  |
Publisher
Related Links
- Metric Tensor-Wolfram MathWorld
- The Wolfram Physics Project
- Stephen Wolfram's A New Kind of Science | Online
- Multiway System–Wolfram MathWorld
Version History
- 1.0.0 – 09 January 2023
Source Metadata
Related Resources
Related Symbols
License Information
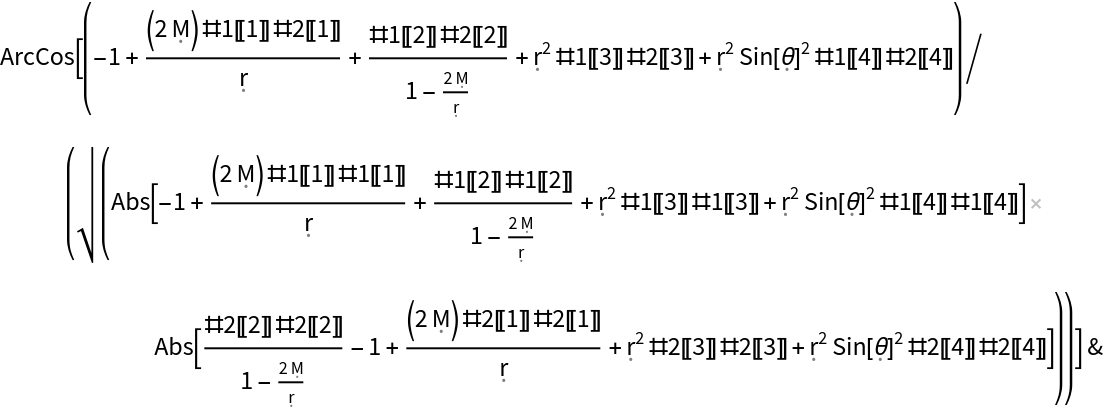This work is licensed under a Creative Commons Attribution 4.0 International License