Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Import and work with a Metamath database
ResourceFunction["MetamathImport"][src] imports Metamath source code from src and returns a MetamathObject with various properties. |
| "Verify" | False | whether to verify theorem proofs or not |
| "Symbols" | list of symbols |
| "Constants" | list of constants |
| "Variables" | list of variables |
| "Statements" | list of statements |
| "Axioms" | list of axioms |
| "Definitions" | list of definitions (axioms starting with "df-") |
| "Theorems" | list of theorems |
| "SymbolCount" | number of symbols |
| "ConstantCount" | number of constants |
| "VariableCount" | number of variables |
| "StatementCount" | number of statements |
| "AxiomCount" | number of axioms |
| "DefinitionCount" | number of definitions |
| "TheoremCount" | number of theorems |
| "DependencyGraph" | theorem proof dependency graph |
| "Proof", thm | proof of a theorem as a list of steps |
| "ProofTree", thm | proof tree of a theorem |
| "ExpandedProofTree", thm | proof tree expanded down to axioms |
| "ProofGraph", thm | proof graph of a theorem |
| "ExpandedProofGraph", thm | proof graph expanded down to axioms |
| "TokenEventGraph", thm | token event proof graph of a theorem |
| "ExpandedTokenEventGraph", thm | token event proof graph expanded down to axioms |
| "SyntaxTree", stmt | syntax breakdown tree of a statement |
| "SyntaxDependencyTree", stmt | syntax dependency tree of a statement |
| "SimpleSyntaxTree", stmt | simplified syntax tree |
| "Import", src | parse and append new Metamath statements |
| "SetMM" | set.mm database |
| "iSetMM" | intuitionistic logic and set theory isetmm database |
| "Peano" | Peano arithmetic peano.mm database |
| "NormMegillWolframAxioms" | Norm Megill's proofs of Sheffer axioms (AxiomaticTheory["ShefferAxioms"]) from the Wolfram Axiom (AxiomaticTheory["WolframAxioms"]) |
| "ASCIITable" | ASCII replacement rules |
Import Metamath source code with a bunch of constants and a simple axiom:
| In[1]:= | ![ResourceFunction["MetamathImport"]["
$c = 0 S 1 $.
wp $a = 0 S 1 $.
"]](https://www.wolframcloud.com/obj/resourcesystem/images/b78/b78a92a5-6ec3-462b-bcdc-a0971c7ea539/1ba494c20159b2c6.png) |
| Out[1]= |
Import a basic Metamath source code sample with 4 constants, 5 variables, 5 floating hypotheses, 1 axiom and 2 proved theorems:
| In[2]:= | ![ResourceFunction["MetamathImport"]["
$c ( ) -> wff $.
$v p q r s t $.
wp $f wff p $.
wq $f wff q $.
wr $f wff r $.
ws $f wff s $.
wt $f wff t $.
w-> $a wff ( p -> q ) $.
w->(->) $p wff ( r -> ( s -> t ) ) $= wr ws wt w-> w-> $.
w(->)-> $p wff ( ( r -> s ) -> t ) $= wr ws w-> wt w-> $.
"]](https://www.wolframcloud.com/obj/resourcesystem/images/b78/b78a92a5-6ec3-462b-bcdc-a0971c7ea539/16e1cfe94c2f817a.png) |
| Out[2]= |
Extract a proof of a theorem:
| In[3]:= |
| Out[3]= |
Construct a proof tree:
| In[4]:= |
| Out[4]= | 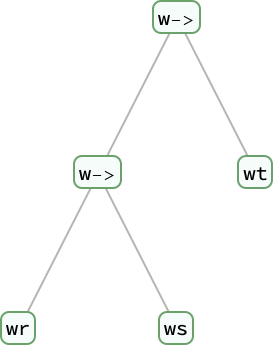 |
Construct a proof graph:
| In[5]:= |
| Out[5]= | 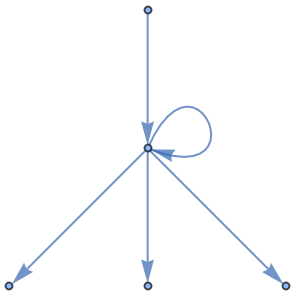 |
Construct a detailed syntax tree breakdown:
| In[6]:= |
| Out[6]= | 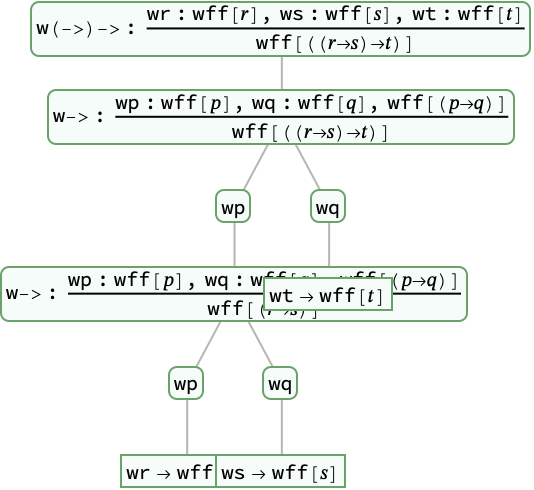 |
Construct a simplified syntax tree:
| In[7]:= |
| Out[7]= |
Introduce a new Metamath theorem by importing a source string and verifying it:
| In[8]:= | ![ResourceFunction["MetamathImport"][
"$( This is the Metamath database demo0.mm. $)\n\n$( Metamath is a formal language and associated computer program for\n archiving, verifying, and studying mathematical proofs, created by Norman\n Dwight Megill (1950--2021). For more information, visit\n https://us.metamath.org and\n https://github.com/metamath/set.mm, and feel free to ask questions at\n https://groups.google.com/g/metamath. $)\n\n$( The database demo0.mm was created by Norman Megill. This is the version\n of 1-Jan-2004. $)\n\n\n$( !\n#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#\n Metamath source file demo0.mm\n#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#\n\n ~~ PUBLIC DOMAIN ~~\nThis work is waived of all rights, including copyright, according to the CC0\nPublic Domain Dedication. https://creativecommons.org/publicdomain/zero/1.0/\n\nNorman Megill - https://us.metamath.org\n\n$)\n\n\n$(\n#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#\n demo0.mm: An introductory formal system example\n#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#*#\n\n This file is the introductory formal system example described in Chapter 2 of\n the Metamath book.\n\n$)\n\n$( Declare the constant symbols we will use. $)\n $c 0 + = -> ( ) term wff |- $.\n\n$( Declare the metavariables we will use. $)\n $v t r s P Q $.\n\n$( Specify properties of the metavariables. $)\n tt $f term t $.\n tr $f term r $.\n ts $f term s $.\n wp $f wff P $.\n wq $f wff Q $.\n\n $( Define \"term\" (part 1 of 2). $)\n tze $a term 0 $.\n\n $( Define \"term\" (part 2 of 2). $)\n tpl $a term ( t + r ) $.\n\n $( Define \"wff\" (part 1 of 2). $)\n weq $a wff t = r $.\n\n $( Define \"wff\" (part 2 of 2). $)\n wim $a wff ( P -> Q ) $.\n\n $( State Axiom ~ a1 . $)\n a1 $a |- ( t = r -> ( t = s -> r = s ) ) $.\n\n $( State Axiom ~ a2 . $)\n a2 $a |- ( t + 0 ) = t $.\n\n ${\n min $e |- P $.\n maj $e |- ( P -> Q ) $.\n $( Define the modus ponens inference rule. $)\n mp $a |- Q $.\n $}"]["Import", "
th1 $p |- t = t $=
tt tze tpl tt weq tt tt weq tt a2 tt tze tpl tt weq tt tze tpl tt weq tt tt
weq wim tt a2 tt tze tpl tt tt a1 mp mp $.
", "Verify" -> True]["Statements"][[-1]]](https://www.wolframcloud.com/obj/resourcesystem/images/b78/b78a92a5-6ec3-462b-bcdc-a0971c7ea539/609c8dba36e72ff7.png) |
| Out[8]= | 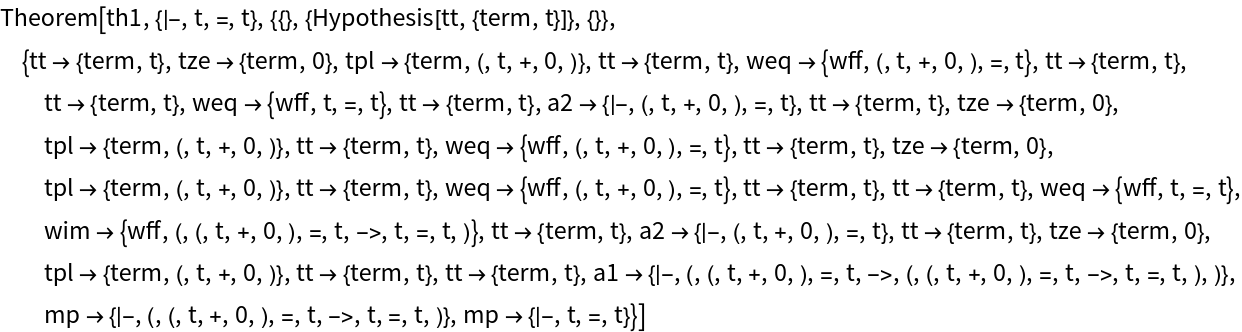 |
Verifying theorems expands proofs with more information:
| In[9]:= | ![Cases[ResourceFunction["MetamathImport"][
"\n$c ( ) -> wff $.\n$v p q r s t $.\nwp $f wff p $.\nwq $f wff q $.\nwr $f wff r $.\nws $f wff s $.\nwt $f wff t $.\nw-> $a wff ( p -> q ) $.\nw->(->) $p wff ( r -> ( s -> t ) ) $= wr ws wt w-> w-> $.\nw(->)-> $p wff ( ( r -> s ) -> t ) $= wr ws w-> wt w-> $.\n", "Verify" -> False]["Statements"], "Theorem"[label_, _, _, proof_] :> label -> proof]](https://www.wolframcloud.com/obj/resourcesystem/images/b78/b78a92a5-6ec3-462b-bcdc-a0971c7ea539/614d9239d55ff334.png) |
| Out[9]= |
| In[10]:= | ![Cases[ResourceFunction["MetamathImport"][
"\n$c ( ) -> wff $.\n$v p q r s t $.\nwp $f wff p $.\nwq $f wff q $.\nwr $f wff r $.\nws $f wff s $.\nwt $f wff t $.\nw-> $a wff ( p -> q ) $.\nw->(->) $p wff ( r -> ( s -> t ) ) $= wr ws wt w-> w-> $.\nw(->)-> $p wff ( ( r -> s ) -> t ) $= wr ws w-> wt w-> $.\n", "Verify" -> True]["Statements"], "Theorem"[label_, _, _, proof_] :> label -> proof]](https://www.wolframcloud.com/obj/resourcesystem/images/b78/b78a92a5-6ec3-462b-bcdc-a0971c7ea539/10572ec3d6ff721e.png) |
| Out[10]= |
Verify Norm Megill's proofs of Sheffer axioms using the Wolfram axioms:
| In[11]:= |
| Out[11]= |  |
Import the SetMM database and explore various visualizations of its theorems:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |  |
| In[14]:= |
| Out[14]= | 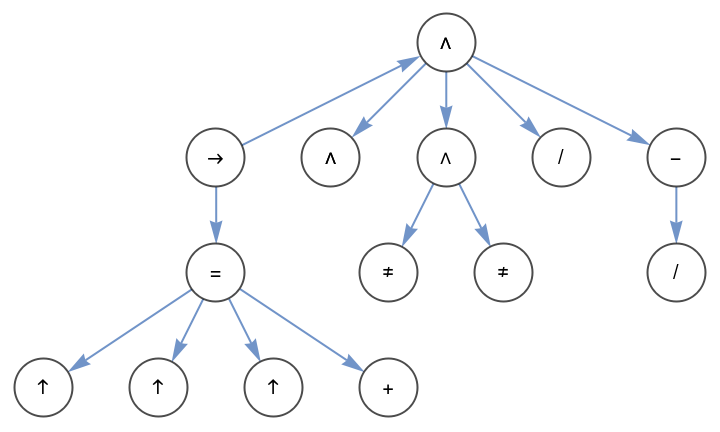 |
| In[15]:= |
| Out[15]= | 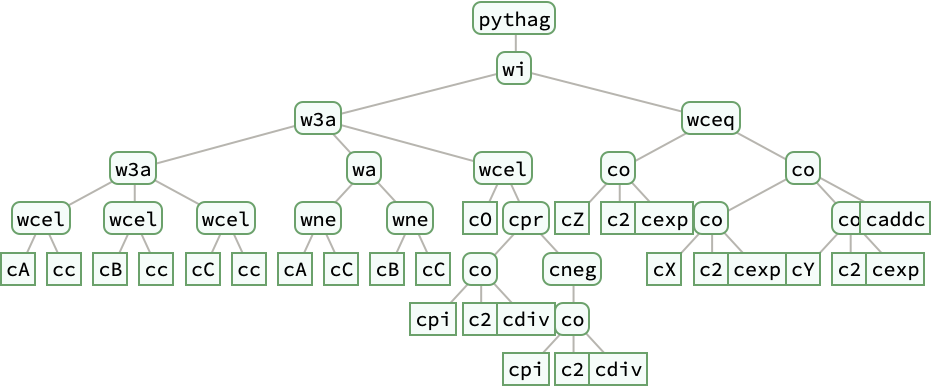 |
| In[16]:= |
| Out[16]= | 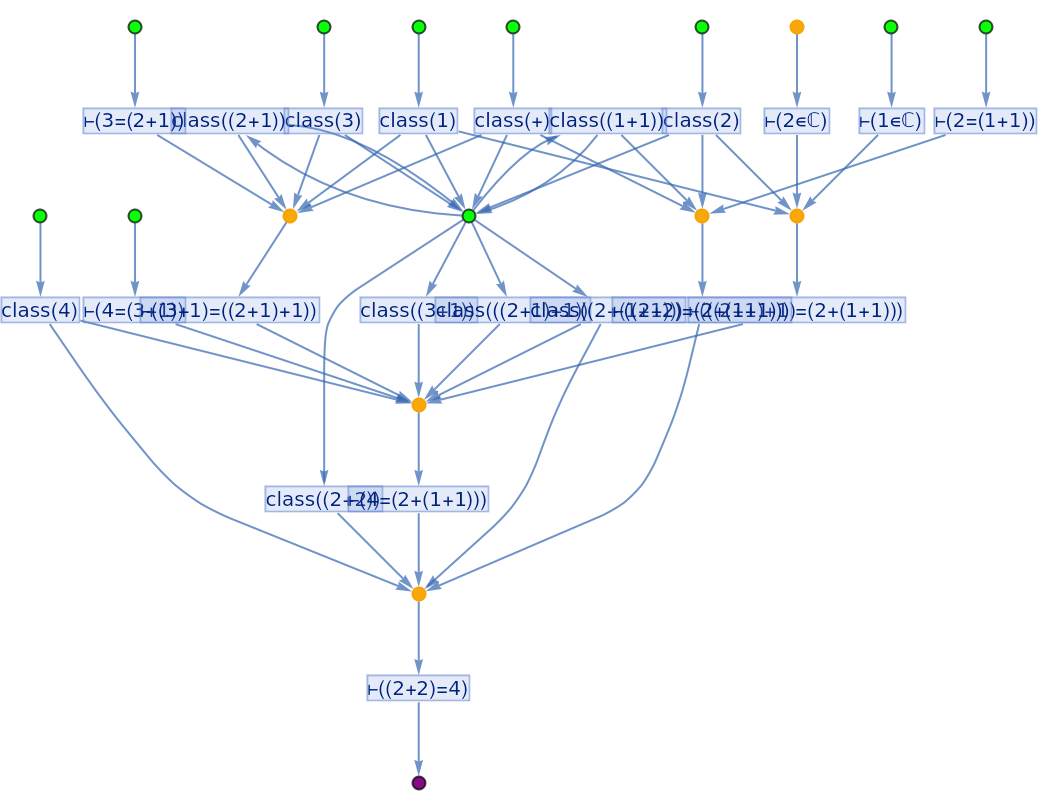 |
| In[17]:= |
| Out[17]= | 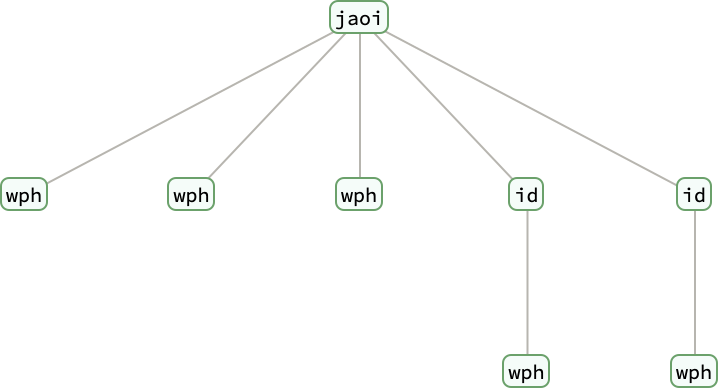 |
Norm Megill's proofs of the Sheffer axioms from the Wolfram Axiom:
| In[18]:= |
| Out[18]= |
| In[19]:= |
| Out[19]= | 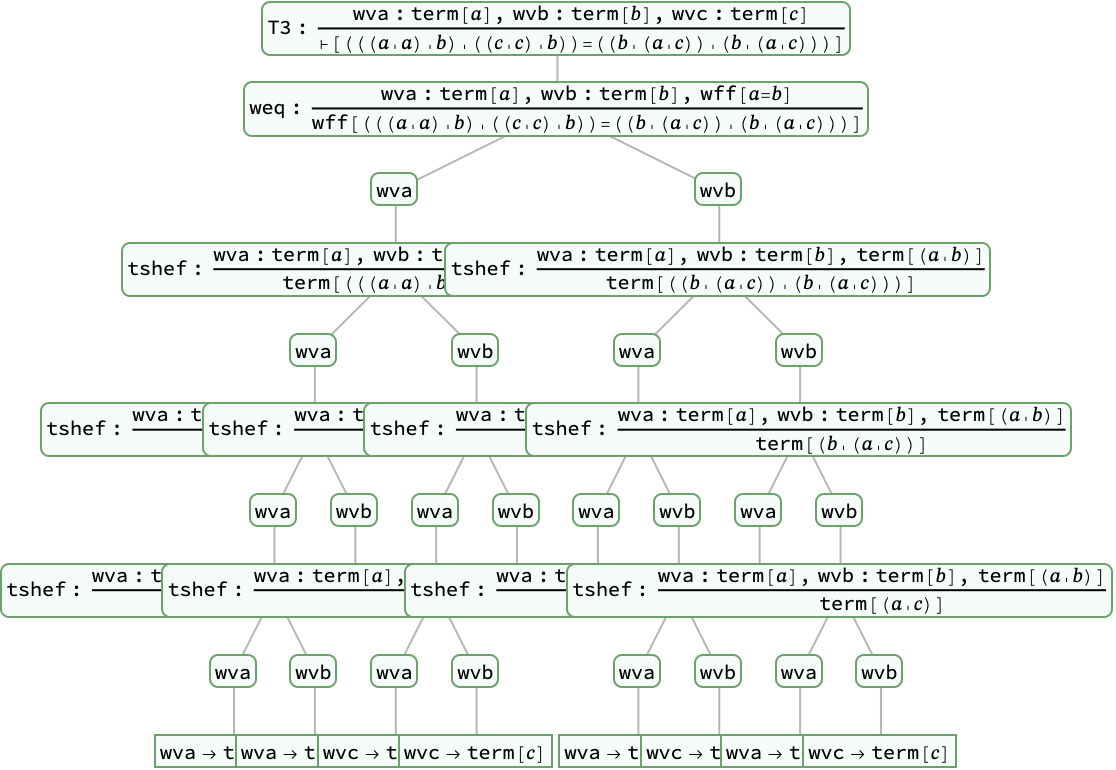 |
| In[20]:= |
| Out[20]= |  |
| In[21]:= |
| Out[21]= | 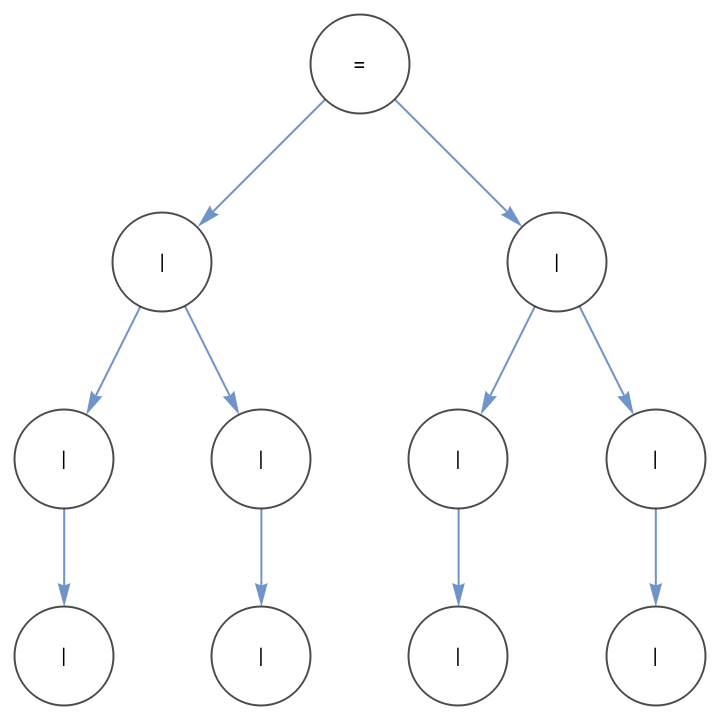 |
This work is licensed under a Creative Commons Attribution 4.0 International License