Basic Examples (2) 

Compute the entropy of a hex mesh:

In[1]:=

Out[1]=

Generate a set of points arranged in a square lattice:

In[2]:=

Out[2]=

Generate the associated mesh region:

In[3]:=

Out[4]=

The resulting Voronoi entropy equals zero:

In[5]:=

Out[5]=

Scope (2) 

A Voronoi tessellation built from slightly distorted hexagons has a corresponding entropy equal to zero, since there is only one kind of polygon (P₁=1; ln P₁=0).

In[6]:=

Out[6]=

Generate lattice points from the basis plus distortion:

In[7]:=

Out[7]=

Create a mesh:

In[8]:=

Out[9]=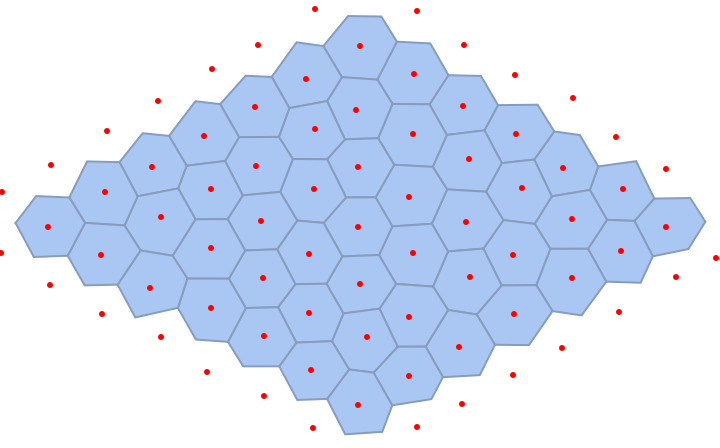

In[10]:=

Out[10]=

Applications (3) 

A semi-regular set of points obtained by alternatively deleting sites from a square lattice gives a twin-tile tessellation with regular hexagons and smaller squares:

In[11]:=

Out[5]=

Generate the corresponding mesh:

In[12]:=

Out[7]=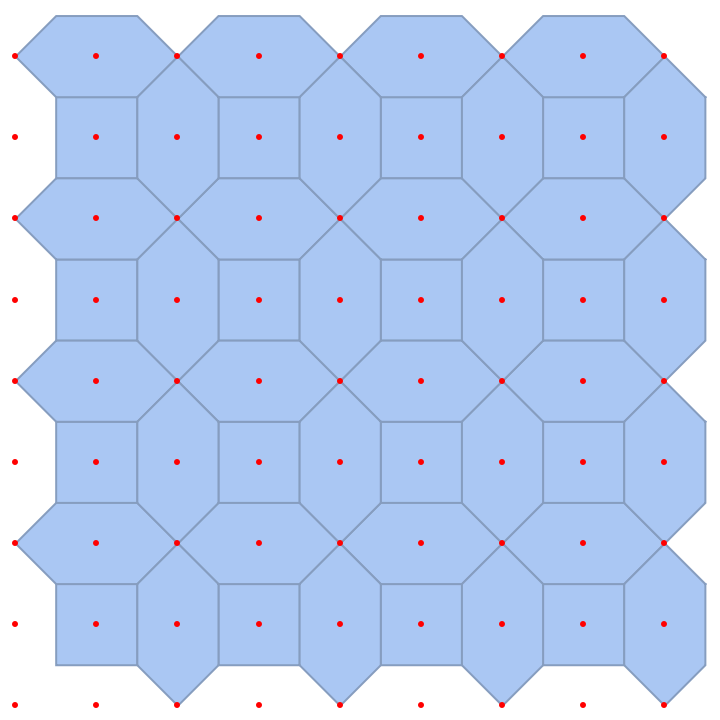

The Voronoi entropy is =0.6365:

In[13]:=

Out[13]=

Properties and Relations (5) 

A hexagonal lattice basis:

In[14]:=

Out[14]=

Add distortions:

In[15]:=

Out[15]=

Create an irregular hexagonal mesh:

In[16]:=

Out[17]=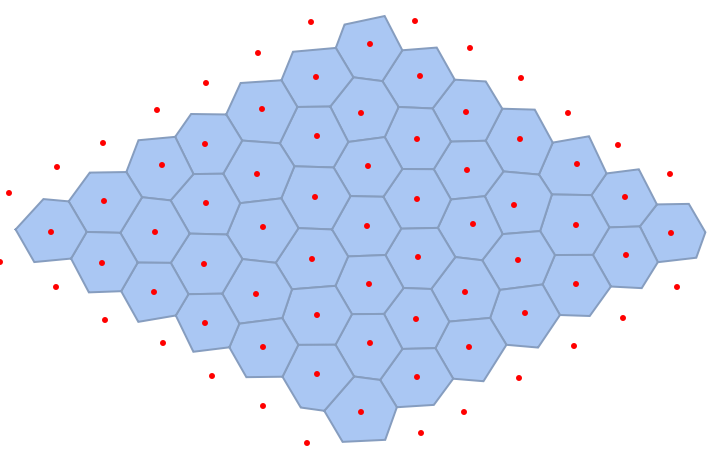

A Voronoi tessellation built from slightly distorted hexagons has a corresponding entropy still equal to zero, since there is only one kind of polygon (P₁=1; ln P₁=0):

In[18]:=

Out[18]=

By increasing the distortion, the Voronoi entropy increases in value:

In[19]:=

In[20]:=

Out[21]=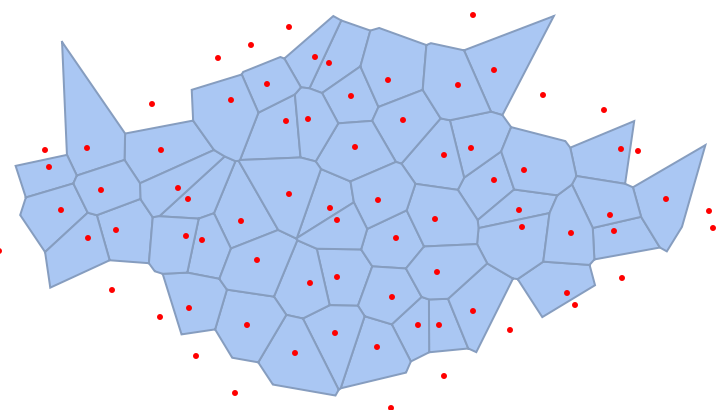

In[22]:=

Out[22]=

Neat Examples (3) 

Create a 2D set of points obtained from a spatial Poisson point process:

In[23]:=

Out[26]=

Generate a Voronoi mesh and show it along with the points:

In[27]:=

Out[27]=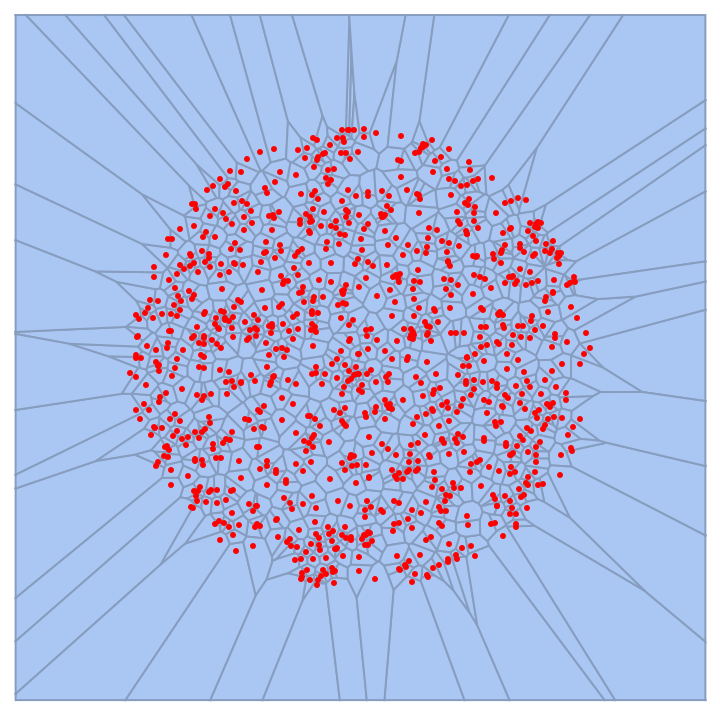

The Voronoi entropy is S_{{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {vor}]}]}}=1.71 according to the value reported in the literature for a randomly distributed set of points:

In[28]:=

Out[28]=