Function Repository Resource:

MergeFindSet

Source Notebook

Provide a merge-find set data structure with standard operations

Contributed by: Daniel Lichtblau

ResourceFunction["MergeFindSet"][init,"Initialize"]

uses the value or values from init to initialize a merge-find set.

ResourceFunction["MergeFindSet"][mfs,j,"Find"]

gives the canonical value associated to element j in the merge-find set mfs.

ResourceFunction["MergeFindSet"][mfs,j,k,"Merge"]

merges the subsets from mfs containing elements j and k provided they are distinct.

Details

A merge-find set is a data structure that contains disjoint subsets of a master set indexed by integers 1…n. It supports both fast finding of canonical subset elements and fast merging of subsets.

A merge-find set is also called a disjoint-set or a union-find set.

Merge-find sets are used in graph partitioning algorithms to keep track of unconnected components as they are merged. One such application is in efficient implementations of Kruskal's minimum spanning tree algorithm.

ResourceFunction["MergeFindSet"] only works with explicit indices 1…n. A more general one can handle arbitrary set elements, though at the expense of speed and memory requirements.

The initialization can specify either a positive integer n or a disjoint partition of Range[n]. In the former case, the initial subsets are singletons containing the individual integers from 1 to n.

Each subset in a merge-find set has a canonical leader element. Elements that are not leaders have parents.

A leader for a given element is located by following the parent path beginning at that element. A leader is its own parent and this gives a termination condition for locating an elements leader.

A merge-set with n elements is comprised of n pairs of integers. The k^th element is {p_k,s_k}, where p_k is the parent of k. When k is its own parent, s_k gives the total size of its subset; it is not used in other cases.

In "Merge" operations, smaller subsets are merged into larger.

Whenever a "Find" is performed, elements in the parent path that do not point directly to the leader will be changed to point directly to it.

ResourceFunction["MergeFindSet"] with one argument will automatically assume the operation is "Initialize".

ResourceFunction["MergeFindSet"][mfs,j] for integer j will automatically assume the operation is "Find".

ResourceFunction["MergeFindSet"][mfs,j,k] for integers j and k will automatically assume the operation is "Merge".

The "Find" operation will thread over its second argument.

ResourceFunction["MergeFindSet"] has the attribure HoldFirst.

Examples

Basic Examples (5)

Initialize a merge-find set with eight elements and show the data:

In[1]:=

Out[1]=

Merge the subsets containing respectively the second and third elements:

In[2]:=

Out[2]=

Successively merge the subsets containing the fourth and fifth elements and then the second and fifth elements:

In[3]:=

ResourceFunction["MergeFindSet"][mfs, 4, 5, "Merge"];
ResourceFunction["MergeFindSet"][mfs, 2, 5, "Merge"];
mfs

Out[3]=

Find the leader of the subset containing the fifth element:

In[4]:=

Out[4]=

Notice that this find operation caused the fifth to point directly to its leader:

In[5]:=

Out[5]=

Scope (7)

In[6]:=

Out[6]=

Find the leaders of the first and last elements:

In[7]:=

Out[7]=

Merge the first and last elements:

In[8]:=

Out[8]=

Check that the last element now has the same leader as the first:

In[9]:=

Out[9]=

Notice that the last now has the same leader as the first:

In[10]:=

Out[10]=

Now merge the second and second-to-last elements:

In[11]:=

Out[11]=

Merge the tenth and eleventh elements:

In[12]:=

Out[12]=

All elements now have the same leader, so the subsets are merged into one set:

In[13]:=

Out[13]=

Properties and Relations (4)

Merging all elements is not measurably worse than O(n) in speed.

Merge all elements into one set by merging consecutive pairs, doubling the pair size until finished:

In[14]:=

$n = 15; msf = ResourceFunction["MergeFindSet"][2^n, "Initialize"]; Timing[Do[ ResourceFunction["MergeFindSet"][msf, i, i + 2^m - 1, "Merge"], {m, 1, n}, {i, 1, 2^n - 1, 2^m}];]$

Out[14]=

Double the size:

In[15]:=

$n += 1; msf = ResourceFunction["MergeFindSet"][2^n, "Initialize"]; Timing[Do[ ResourceFunction["MergeFindSet"][msf, i, i + 2^m - 1, "Merge"], {m, 1, n}, {i, 1, 2^n - 1, 2^m}];]$

Out[15]=

Double the size again:

In[16]:=

$n += 1; msf = ResourceFunction["MergeFindSet"][2^n, "Initialize"]; Timing[Do[ ResourceFunction["MergeFindSet"][msf, i, i + 2^m - 1, "Merge"], {m, 1, n}, {i, 1, 2^n - 1, 2^m}];]$

Out[16]=

We see substantially the same speed if we merge successively with the first element:

In[17]:=

$msf = ResourceFunction["MergeFindSet"][2^n, "Initialize"]; Timing[Do[ ResourceFunction["MergeFindSet"][msf, 1, i, "Merge"], {i, 2, 2^n}];]$

Out[17]=

Applications (2)

Minimum Spanning Trees: Kruskal's algorithm (2)

A minimum spanning tree for a connected graph is a tree that hits every vertex, has no cycles and is of minimal total edge weight. Kruskal's method for computing the minimum spanning tree of a connected, weighted undirected graph works as follows. Start with the set of all vertices and no connections. Add connecting edges in order of length provided they are between two vertices that are not yet connected. At each such step, merge the connected subsets containing the two respective vertices. It has algorithmic complexity O(e log(e)) where e is the number of edges. We do this for the special case where of a complete graph given by a set of points in the plane, with edge weights being the distances between vertices.

The following code implements Kruskal's algorithm:

In[18]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e68fae57-0257-4253-9e5f-e896a88bf6e3"]

Create random points in the plane:

In[19]:=

Out[19]=

Use Kruskal's method to compute their minimum spanning tree:

In[20]:=

Out[20]=

Show the graph of the spanning tree:

In[21]:=

Out[21]=

For n vertices, we have edges. The time complexity of Kruskal's method is O(e log(e)). The space requirement is O(e).

Use Kruskal's method on a larger point set:

In[22]:=

BlockRandom[SeedRandom[1234];
nverts = 200;
ListPlot[pts = RandomReal[{-10, 10}, {nverts, 2}], AspectRatio -> Automatic]]

Out[22]=

Compute the minimal spanning tree:

In[23]:=

Out[23]=

Show the total branch length of this spanning tree:

In[24]:=

Out[24]=

Show the spanning tree:

In[25]:=

Out[25]=

Double the size of the point set:

In[26]:=

nverts = 400;
pts = RandomReal[{-10, 10}, {nverts, 2}];
Timing[{tdist, treegraph} = Kruskal[pts];]

Out[26]=

Show the spanning tree:

In[27]:=

Out[27]=

The Kruskal method built into FindSpanningTree has the same asymptotic behavior, but is many times faster:

In[28]:=

edges = Flatten[
Table[UndirectedEdge[i, j], {i, nverts - 1}, {j, i + 1, nverts}]];
edgeweights = Flatten[Table[
EuclideanDistance[pts[[i]], pts[[j]]], {i, nverts - 1}, {j, i + 1,
nverts}]];
gr = Graph[Range[nverts], edges, EdgeWeight -> edgeweights, VertexCoordinates -> pts];
Timing[msk = FindSpanningTree[gr, Method -> "Kruskal"]]

Out[28]=

Timing ratios over several doublings of the vertex count (hence quadrupling the edge counts) shows the asymptotic behaviors are comparable:

In[29]:=

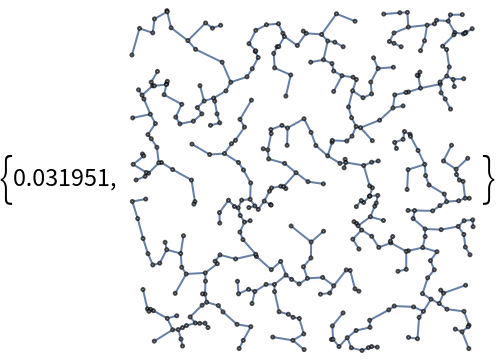
$Table[nverts = 2^n; pts = RandomReal[{-10, 10}, {nverts, 2}]; t1 = First[Timing[{tdist, treegraph} = Kruskal[pts]]]; edges = Flatten[ Table[UndirectedEdge[i, j], {i, nverts - 1}, {j, i + 1, nverts}]]; edgeweights = Flatten[Table[ EuclideanDistance[pts[[i]], pts[[j]]], {i, nverts - 1}, {j, i + 1, nverts}]]; gr = Graph[Range[nverts], edges, EdgeWeight -> edgeweights, VertexCoordinates -> pts]; t2 = First[Timing[msp = FindSpanningTree[gr, Method -> "Kruskal"]]]; {t1/t2}, {n, 7, 11}]$

Out[29]=

Version History

1.0.0 – 05 April 2021

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

MergeFindSet

Details