Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Express MeijerG expressions in terms of HypergeometricPFQ
ResourceFunction["MeijerGToHypergeometricPFQ"][expr] converts MeijerG expressions in expr to a form involving HypergeometricPFQ. | |
ResourceFunction["MeijerGToHypergeometricPFQ"][expr,f] wraps f around any HypergeometricPFQ head in the result. |
A Meijer G-function:
| In[1]:= |
| Out[1]= |
Expand in terms of generalized hypergeometric functions:
| In[2]:= |
| Out[2]= | 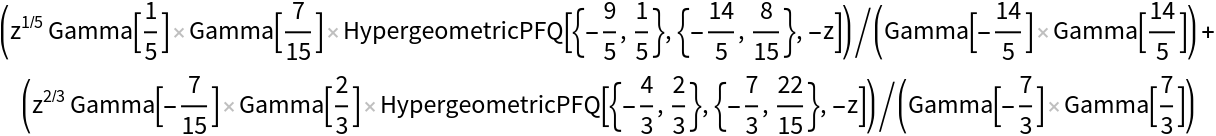 |
Verify that the two expressions are equivalent:
| In[3]:= |
| Out[3]= |
A generalized Meijer G-function:
| In[4]:= |
| Out[4]= |
Generate the hypergeometric representation:
| In[5]:= |
| Out[5]= |  |
Use MeijerGReduce to convert a special function to its equivalent MeijerG representation:
| In[6]:= |
| Out[6]= |
The result after conversion with MeijerGToHypergeometricPFQ does not have HypergeometricPFQ terms due to autoevaluation:
| In[7]:= |
| Out[7]= | 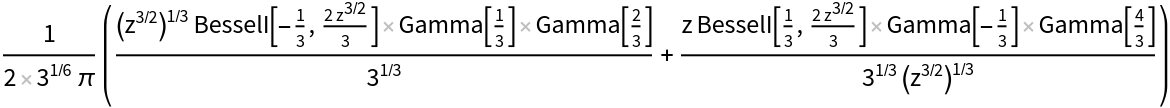 |
Wrap the HypergeometricPFQ heads in Inactive to prevent evaluation:
| In[8]:= |
| Out[8]= | 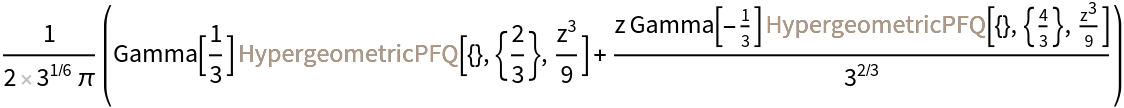 |
FunctionExpand always tries to convert to simpler functions whenever possible:
| In[9]:= |
| Out[9]= | 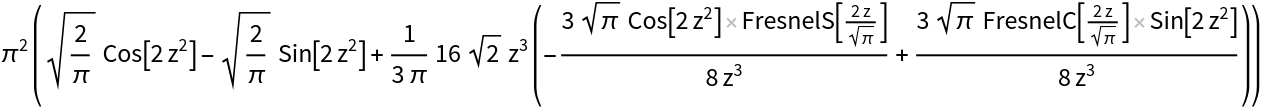 |
MeijerGToHypergeometricPFQ performs a less drastic conversion:
| In[10]:= |
| Out[10]= | 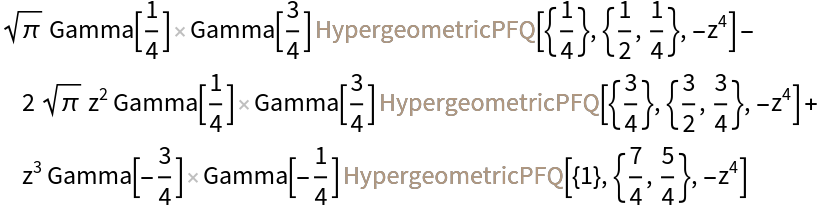 |
If Inactive is not supplied as the second argument, the resulting HypergeometricPFQ expressions might still autoevaluate:
| In[11]:= |
| Out[11]= | 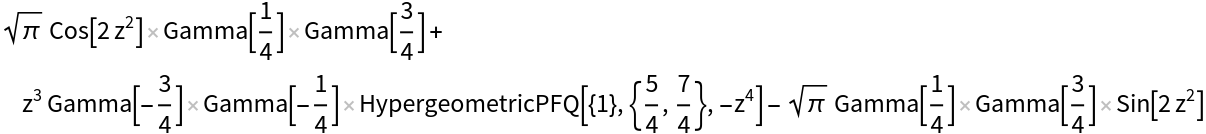 |
MeijerG expressions that autoevaluate cannot be directly converted:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
Wrap MeijerG in Inactive and use Inactive as the second argument to prevent evaluation:
| In[14]:= |
| Out[14]= |
Use Activate to see the simpler expression:
| In[15]:= |
| Out[15]= |
Piecewise results can be returned in some cases:
| In[16]:= |
| Out[16]= |  |
Logarithmic cases will not be converted:
| In[17]:= |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License