Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MeijerGForm

Source Notebook

Convert a mathematical expression into an equivalent expression with head MeijerG

Contributed by: Paco Jain & Oleg Marichev

ResourceFunction["MeijerGForm"][f,z]

expresses the function f, written in terms of the independent variable z, in terms of MeijerG when possible.

Details

The result of MeijerG form will either return the original expression, or one involving Inactive[MeijerG]. The Inactive wrapper is to prevent auto-evaluation of MeijerG into simpler functions, and can be removed with Activate.

Examples

Basic Examples (2) 

Get the Meijer-G form of a trigonometric function:

In[1]:=
ResourceFunction["MeijerGForm"][Sin[z], z]
Out[1]=

Activating the result allows the MeijerG to evaluate, giving back the original function:

In[2]:=
Activate[%]
Out[2]=

Represent BesselJ in terms of MeijerG:

In[3]:=
ResourceFunction["MeijerGForm"][BesselJ[1, a x], x]
Out[3]=

Recover the original function using Activate:

In[4]:=
Activate[%]
Out[4]=

Scope (10) 

Elementary Functions (5) 

Rational functions:

In[5]:=
ResourceFunction["MeijerGForm"][1/(x^2 + 1), x]
Out[5]=
In[6]:=
ResourceFunction["MeijerGForm"][1/(2 x + 3), x]
Out[6]=

Algebraic functions:

In[7]:=
ResourceFunction["MeijerGForm"][1/(Sqrt[x] + 1), x]
Out[7]=

Trigonometric functions:

In[8]:=
ResourceFunction["MeijerGForm"][Sin[a x], x]
Out[8]=
In[9]:=
ResourceFunction["MeijerGForm"][Cos[a x + d], x]
Out[9]=

Linear combination of trigonometric functions:

In[10]:=
ResourceFunction["MeijerGForm"][2 Sin[x] + Cos[x], x]
Out[10]=

Inverse trigonometric and hyperbolic functions:

In[11]:=
ResourceFunction["MeijerGForm"][ArcSin[x], x]
Out[11]=
In[12]:=
ResourceFunction["MeijerGForm"][ArcTanh[x], x]
Out[12]=

Special Functions (5) 

Airy functions:

In[13]:=
ResourceFunction["MeijerGForm"][AiryAi[x], x]
Out[13]=
In[14]:=
ResourceFunction["MeijerGForm"][AiryBi[x], x]
Out[14]=

Bessel functions:

In[15]:=
ResourceFunction["MeijerGForm"][BesselJ[n, x], x]
Out[15]=
In[16]:=
ResourceFunction["MeijerGForm"][BesselK[n, x], x]
Out[16]=

Legendre functions:

In[17]:=
ResourceFunction["MeijerGForm"][LegendreQ[n, x], x]
Out[17]=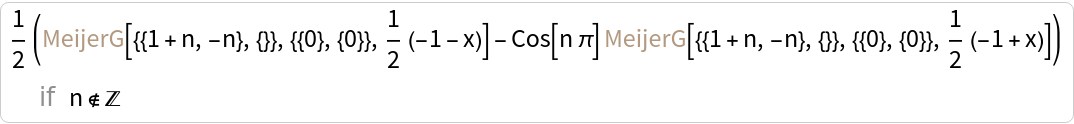

Hypergeometric functions:

In[18]:=
ResourceFunction["MeijerGForm"][Hypergeometric2F1[a, b, c, x], x]
Out[18]=

Elliptic integrals:

In[19]:=
ResourceFunction["MeijerGForm"][EllipticK[m], m]
Out[19]=
In[20]:=
ResourceFunction["MeijerGForm"][EllipticE[m], m]
Out[20]=

Properties and Relations (1) 

If a MeijerG representation cannot be found, the function returns unevaluated:

In[21]:=
ResourceFunction["MeijerGForm"][Sqrt[1 - Cosh[z]], z]
Out[21]=

Publisher

Wolfram|Alpha Math Team

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.2.1 – 05 April 2024
  • 1.2.0 – 14 August 2023
  • 1.1.2 – 07 November 2022
  • 1.1.1 – 10 October 2022
  • 1.1.0 – 10 October 2022
  • 1.0.0 – 23 August 2022

Related Resources

Author Notes

To view the full source code for this and related functions, evaluate the following:

In[1]:=
SystemOpen[ DirectoryName[ FindFile["WolframAlphaMath`SpecialFunctionsAndCalculus`"]]]

License Information