Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create a beta distribution using the mean and a measure of its spread as parameters instead of using the conventional parameters
ResourceFunction["MeanSpreadBetaDistribution"][mean,spread] creates a beta distribution that is centered at mean and with standard deviation of spread multiplied by the maximum possible standard deviation for mean. |
Create a beta distribution whose mean is 2/3 and whose standard deviation is 1/2 of the maximum possible value given that mean:
| In[1]:= |
| Out[1]= |
Create a beta distribution whose mean is 1/4 and whose standard deviation is 9/10 of the maximum possible value given that mean:
| In[2]:= |
| Out[2]= |
The function handles symbolic parameters:
| In[3]:= |
| Out[3]= |
Show how decreasing the spread of a beta distribution affects the associated PDF :
| In[4]:= | ![Table[Plot[
PDF[ResourceFunction["MeanSpreadBetaDistribution"][0.6, spread], x], {x, 0, 1}, PlotRange -> {0, 10}, PlotLabel -> StringTemplate["spread: `1`"][spread]], {spread, 0.1, 0.9, 0.2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a70/a7013ea6-d14b-4290-a8f8-40943ae4b801/0598c345118796d3.png) |
| Out[4]= | 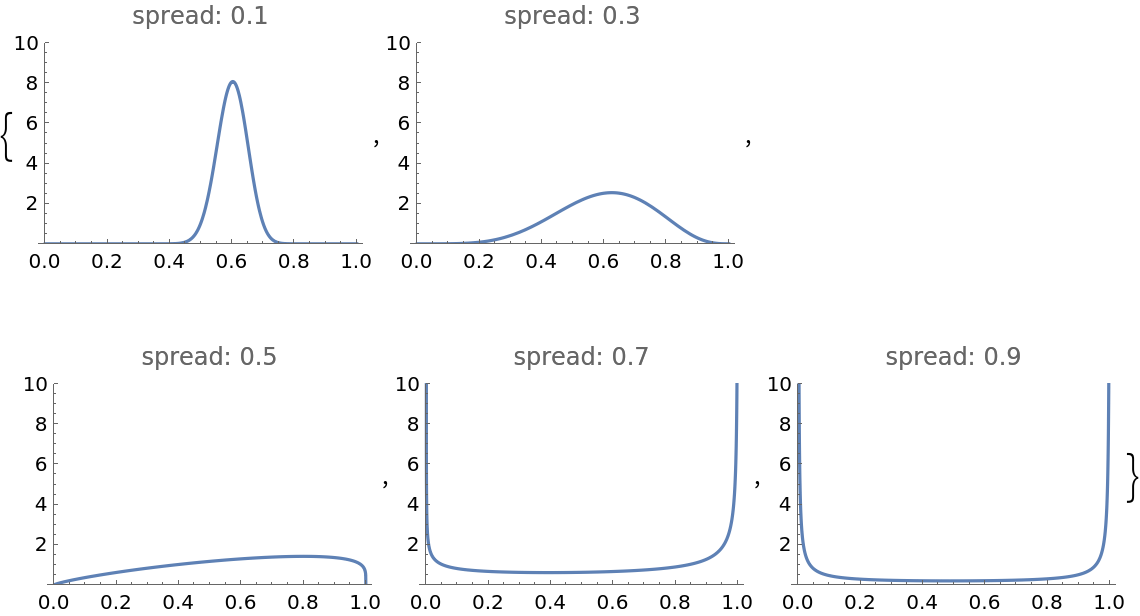 |
One can take the parameters of a beta distribution and compute their mean and spread:
| In[5]:= |
| Out[5]= |
| In[6]:= | ![sol = Solve[
StandardDeviation[BetaDistribution[a, b]] == \[ScriptS]*
StandardDeviation[BetaDistribution[a, 1]], \[ScriptS]]](https://www.wolframcloud.com/obj/resourcesystem/images/a70/a7013ea6-d14b-4290-a8f8-40943ae4b801/2464f00ce2f80b3e.png) |
| Out[6]= |
Thus, for BetaDistribution[3,4] the mean is 3/7 and the spread is calculated below:
| In[7]:= |
| Out[7]= |
If one uses a spread less than zero, the result is a meaningless beta distribution. With a value of greater than one, the result is a meaningless beta distribution with an illegal negative first parameter:
| In[8]:= |
| Out[8]= |
This work is licensed under a Creative Commons Attribution 4.0 International License