Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the mean curvature of a surface
ResourceFunction["MeanCurvature"][s,{u,v}] computes the mean curvature of parametrized surface s with respect to parametrizing variables u and v. | |
ResourceFunction["MeanCurvature"][eq,{x,y,z}] computes the mean curvature of the surface given by the implicit equation eq in variables x,y and z. |
Mean curvature of a sphere:
| In[1]:= |
![ResourceFunction["MeanCurvature"][
Entity["Surface", "Sphere"]["ParametricEquations"][a][u, v], {u, v}] // PowerExpand](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a76a367-5cde-4ab1-9c64-c268fe06529f/0d466157639253ae.png)
|
| Out[1]= |
|
Plot the Kuen surface:
| In[2]:= |
|
| Out[2]= |
|
| In[3]:= |
|
| Out[3]= |
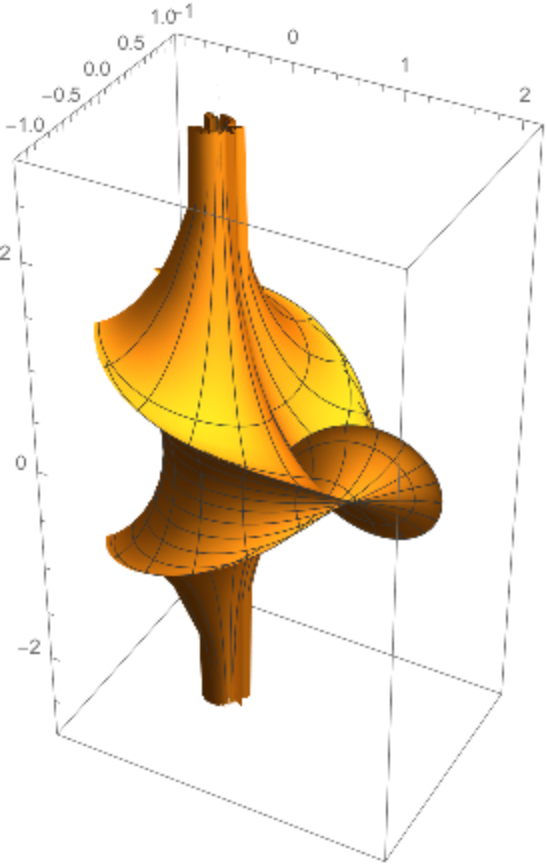
|
Compute its mean curvature:
| In[4]:= |
|
| Out[4]= |
|
Plot the mean curvature:
| In[5]:= |
|
| Out[5]= |
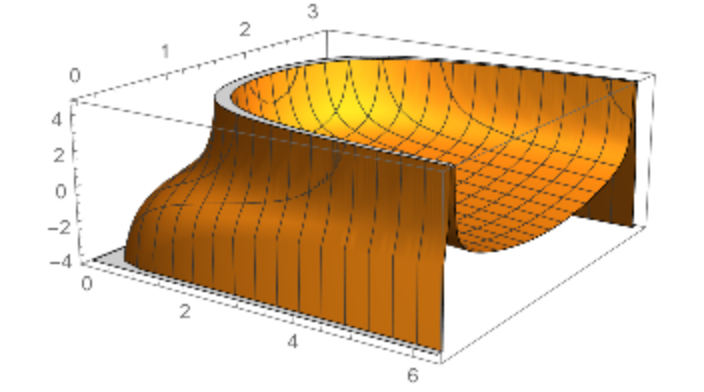
|
Plot the surface with a color function in accordance with the mean curvature:
| In[6]:= |
![range = Last[PlotRange /. AbsoluteOptions[ks, PlotRange]];
ParametricPlot3D[Evaluate[kuen], {u, -4, 4}, {v, 0, \[Pi]}, PlotPoints -> 80, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[mc, range]]], ColorFunctionScaling -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a76a367-5cde-4ab1-9c64-c268fe06529f/44b74e64bb1687fb.png)
|
| Out[6]= |
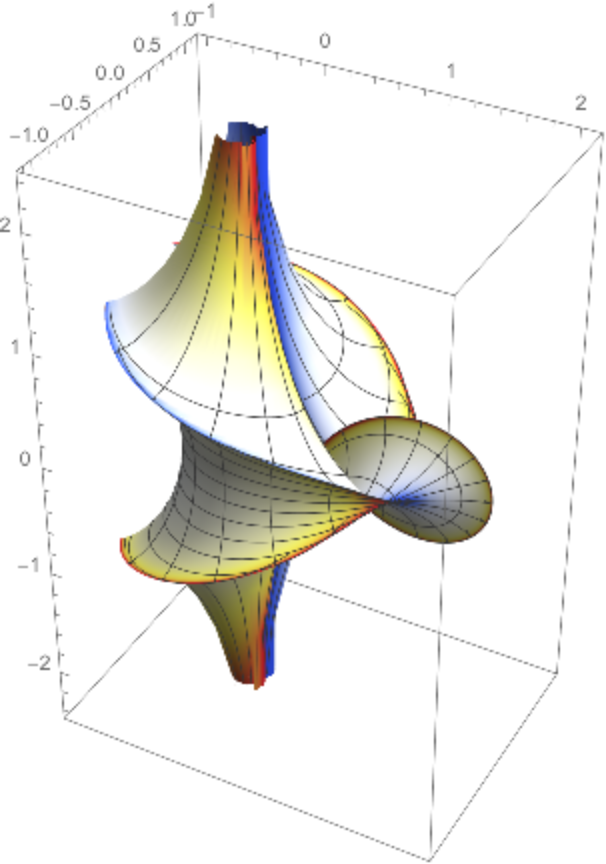
|
The Gaussian curvature is constant:
| In[7]:= |
![cur = ResourceFunction["GaussianCurvature"][
Entity["Surface", "KuenSurface"]["ParametricEquations"][a][u, v], {u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a76a367-5cde-4ab1-9c64-c268fe06529f/2fb9b4965b5a5fdb.png)
|
| Out[7]= |
|
Define the implicit equation for the sine surface:
| In[8]:= |
|
The mean curvature:
| In[9]:= |
|
| Out[9]= |
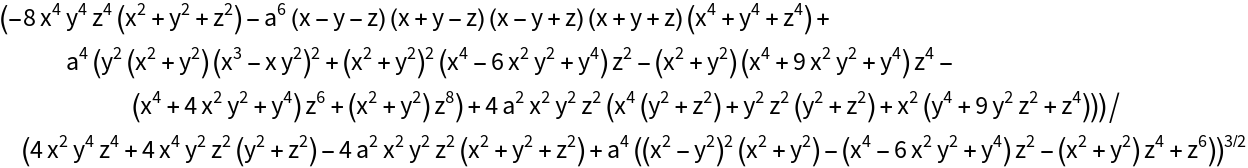
|
| In[10]:= |
|
| Out[10]= |
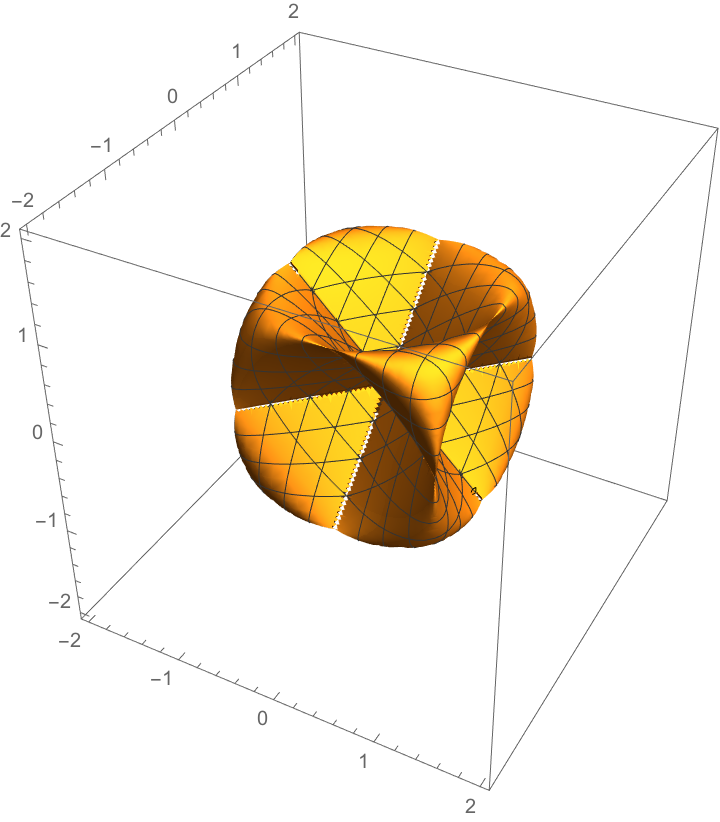
|
The mean curvature of a minimal surface is zero:
| In[11]:= |
|
| Out[11]= |
|
The mean curvature for an implicit surface:
| In[12]:= |
|
| Out[12]= |
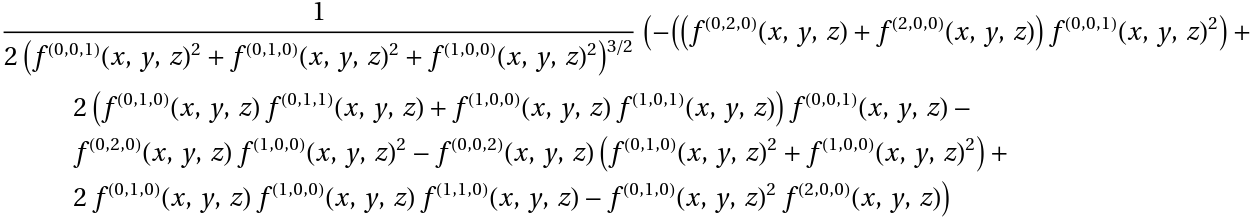
|
The curvature can be obtained for named surfaces using entities:
| In[13]:= |
|
| Out[13]= |
|
The expressions seem to be different, but they are equal:
| In[14]:= |
![FullSimplify[
ResourceFunction["MeanCurvature"][
Entity["Surface", "KuenSurface"]["ParametricEquations"][a][u, v], {u, v}] - Entity["Surface", "KuenSurface"]["MeanCurvature"][a][u, v] // PowerExpand]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a76a367-5cde-4ab1-9c64-c268fe06529f/3dfd6927aa8404d7.png)
|
| Out[14]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License