Function Repository Resource:

MatrixPolynomial

Source Notebook

Evaluate a matrix polynomial

Contributed by: Jan Mangaldan

ResourceFunction["MatrixPolynomial"][p,m]

gives the matrix generated by the polynomial function p at the matrix argument m.

ResourceFunction["MatrixPolynomial"][p,m,v]

gives the matrix generated by the polynomial function p at the matrix argument m, applied to the vector v.

Details

ResourceFunction["MatrixPolynomial"][p,m] effectively evaluates the polynomial function p with ordinary powers replaced by matrix powers.

ResourceFunction["MatrixPolynomial"][{c₀,c₁,…,c_n},m] with scalar c_i takes the polynomial function to be

ResourceFunction["MatrixPolynomial"] works only on square matrices.

ResourceFunction["MatrixPolynomial"] can be used on SparseArray objects.

Examples

Basic Examples (1)

Compute a matrix polynomial, specifying the polynomial as a pure function:

In[1]:=

$ResourceFunction["MatrixPolynomial"][ x |-> x^5 + 2 x^2 + 1, {{a, 1}, {0, b}}]$

Out[1]=

Scope (5)

Evaluate a matrix polynomial with a machine-precision matrix:

In[2]:=

$ResourceFunction["MatrixPolynomial"][ x |-> x^3 - 2 x - 5, {{1.2, 2.5, -3.2}, {0.7, -9.4, 5.8}, {-0.2, 0.3, 6.4}}]$

Out[2]=

The polynomial can be specified as a list of coefficients:

In[3]:=

Out[3]=

Evaluate a matrix polynomial with a complex matrix:

In[4]:=

$ResourceFunction[ "MatrixPolynomial"][#^3 - 2 # - 5 &, {{1. + I, 2, 3 - 2 I}, {0, 4 \[Pi], 5 I}, {E, 0, 6}}]$

Out[4]=

Evaluate a matrix polynomial with an arbitrary-precision matrix:

In[5]:=

$ResourceFunction["MatrixPolynomial"][#^3 - 2 # - 5 &, RandomReal[1, {2, 2}, WorkingPrecision -> 20]]$

Out[5]=

Evaluating a matrix polynomial with a large machine-precision matrix is efficient:

In[6]:=

Out[7]=

Directly applying the matrix polynomial to a single vector is even more efficient:

In[8]:=

Out[9]=

Compute a matrix polynomial applied to a vector for a sparse matrix:

In[10]:=

$ma = SparseArray[{{i_, i_} -> -2., {i_, j_} /; Abs[i - j] == 1 -> 1.}, {10, 10}]; ve = RandomReal[1, 10]; ResourceFunction["MatrixPolynomial"][ x |-> NorlundB[11, 1/2, x], ma, ve]$

Out[12]=

Applications (2)

Evaluate a matrix rational function:

In[13]:=

$rat[x_] = PadeApproximant[E^x, {x, 0, 5}]$

Out[13]=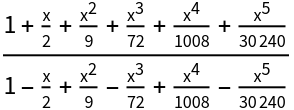

In[14]:=

$num[x_] = Numerator[rat[x]]; den[x_] = Denominator[rat[x]]; ma = RandomReal[1, {4, 4}, WorkingPrecision -> 20]; LinearSolve[ResourceFunction["MatrixPolynomial"][den, ma], ResourceFunction["MatrixPolynomial"][num, ma]]$

Out[17]=

Compare with the result of MatrixFunction:

In[18]:=

Out[18]=

Properties and Relations (2)

MatrixPolynomial is more efficient than MatrixFunction:

In[19]:=

Out[19]=

In[20]:=

Out[20]=

If m is diagonalizable with m=v.d.v^-1 and the eigenvectors are well conditioned, then p(m)=v.p(d).v^-1:

In[21]:=

$poly[x_] = LaguerreL[11, 5/2, x]; ma = RandomReal[1, {4, 4}]; {d, vt} = Eigensystem[ma]$

Out[23]=

In[24]:=

Out[24]=

Neat Examples (1)

Demonstrate the Cayley–Hamilton theorem:

In[25]:=

Out[25]=

In[26]:=

Out[26]=

Version History

1.0.0 – 08 March 2021

Source Metadata

Citation:
- Van Loan C., "A note on the evaluation of matrix polynomials." IEEE Transactions on Automatic Control, vol. 24, no. 2, 320-321, 1979. DOI: 10.1109/TAC.1979.1102005

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License