Basic Examples (3)
Consider a 4×4 matrix, which can be interpreted as an element of space  , i.e. of the tensor product of two subspaces
, i.e. of the tensor product of two subspaces 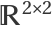 :
:
Calculate the partial trace over the second subspace 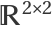 :
:
Calculate a partial trace over multiple subspaces at once:
Calculate a partial trace of a numeric matrix:
Scope (10)
Data types (3)
Calculate a partial trace of a numeric matrix:
Calculate a partial trace of a symbolic matrix:
Calculate a partial trace of a SparseArray:
If the input is a SparseArray, so is the output. This is true even if the resulting array is just a 1×1 array:
Subspace specification (5)
The second argument can contain negative numbers. In that case, the counting goes from the end of the list, in complete analogy to Take specification:
If the partial trace is taken only over one subspace, the second argument can be specified as the index of this subspace:
If the partial trace is to be taken over a range {a,…,b} of successive subspaces, the second argument can be specified as a;;b:
If the partial trace is to be taken over all but one subspace with index k, the second argument can also be specified as Except[k]:
More indices can be specified:
When the second argument is set to All, the partial trace is taken over all subspaces, which corresponds to the standard trace:
Dimension specification (2)
If all subspaces have the same dimension, only this one dimension can be entered instead of the whole list:
Dimensions can be different for different subspaces. However, their product has to be equal to the dimension of the input matrix:
Options (6)
Method (3)
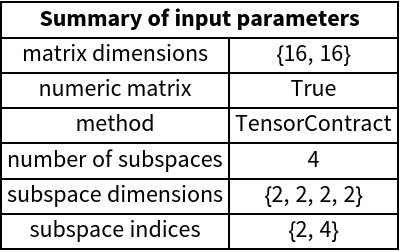
Calculate the partial trace using Mathematica’s built-in function TensorContract. This routine is usually faster for numeric matrices:
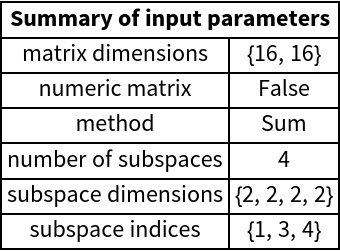
Calculate the partial trace using block-wise summation implemented by Mathematica’s built-in function Sum. This routine is usually faster for symbolic matrices:
By default, the "TensorContract" method is used, when the input matrix is numeric, and the "Sum" method is used when it is symbolic:
Compare the speed of different methods for numeric and symbolic matrices:
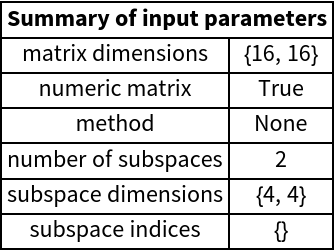
There are two special cases that do not follow the previously stated rules. The first is when the list of subspaces to be traced over is empty. In that case, the input matrix is returned:
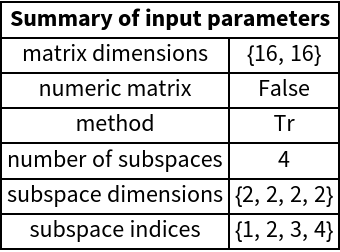
The second case is when the partial trace is to be taken over all subspaces. In that case, Mathematica’s built-in function Tr is used internally instead:
Verbose (3)
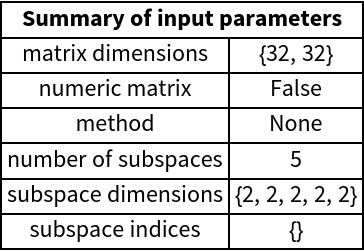
When set to True, there is an additional summary of preprocessed values of parameters printed:
When the second argument is an empty list, the "method" item returns None:
When the second argument is the list of all subspaces, the routine internally uses Tr and the "method" item returns "Tr":
Applications (2)
In quantum mechanics, a partial trace of a density matrix gives the quantum state of a subsystem.
Let ρ12 be a density matrix of a system of two maximally entangled photons in their polarization:
The quantum state of one of the photons is obtained as a partial trace over the state of the other photon. In this case, the resulting state ρ1 is maximally mixed:
The same result is obtained when tracing over the first photon to get the state ρ2 of the second photon:
Generate a random quantum state of three spin-1/2 particles:
Matrix ρ123 is a positive semidefinite matrix with unit trace and thus represents a valid density operator:
The state of the second particle is obtained as the partial trace of ρ123 over the first and third particles:
This matrix again represents a valid density operator:
Properties and Relations (3)
The order in which the subspaces are specified is irrelevant:
Successive applications of a partial trace for different subspaces gives the same results as a single application of a multi-subspace partial trace:
The partial trace over all subspaces corresponds to the standard trace:
Possible Issues (5)
MatrixPartialTrace always returns a matrix, even when the trace is taken over all subspaces:
The trace over all subspaces can be calculated also using Tr, which returns the sum of diagonal elements:
The same is true also when the input matrix is a SparseArray:
When both positive and negative indices are used in the second argument, it might happen that multiple indices refer to the same subspace. This case is nevertheless not allowed:
For some settings of the initial index, final index, and the step in the Span specification, undesired behavior may occur:
Use "Verbose"→True to see how the input parameters are interpreted:
When the indices to be excluded from the tracing are out of the valid range, the trace is done over all subspaces:
Note that when tracing over multiple subspaces one by one, the position and dimensions of subspaces in each new application of the partial traces may change:
When the tracing proceeds from the end of the list of positions, here {1,2}, no recalculation of subspace positions is necessary:
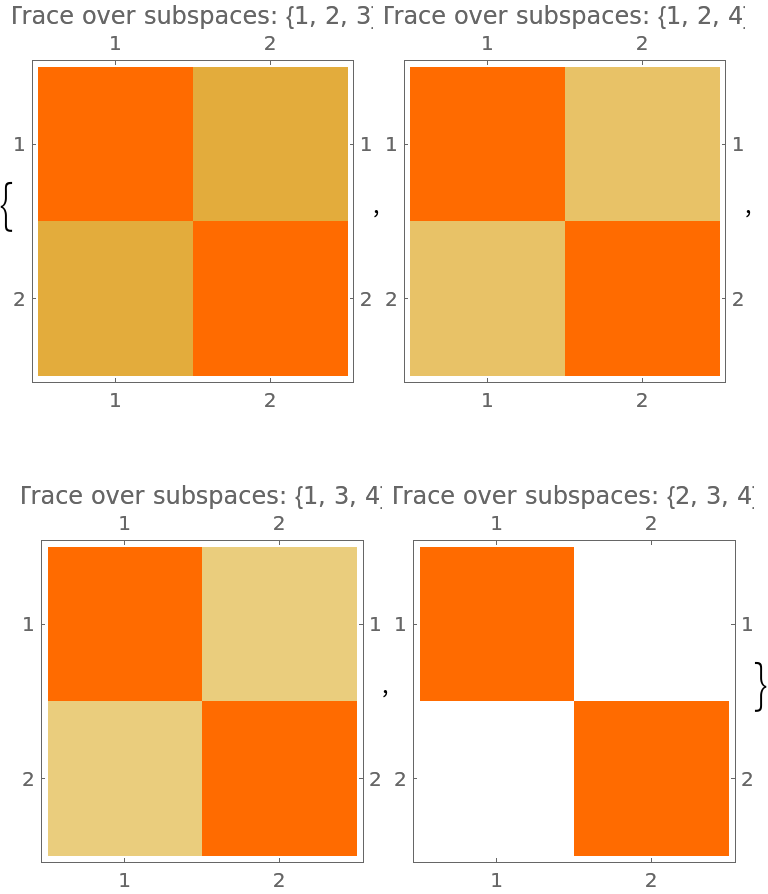
Neat Examples (1)
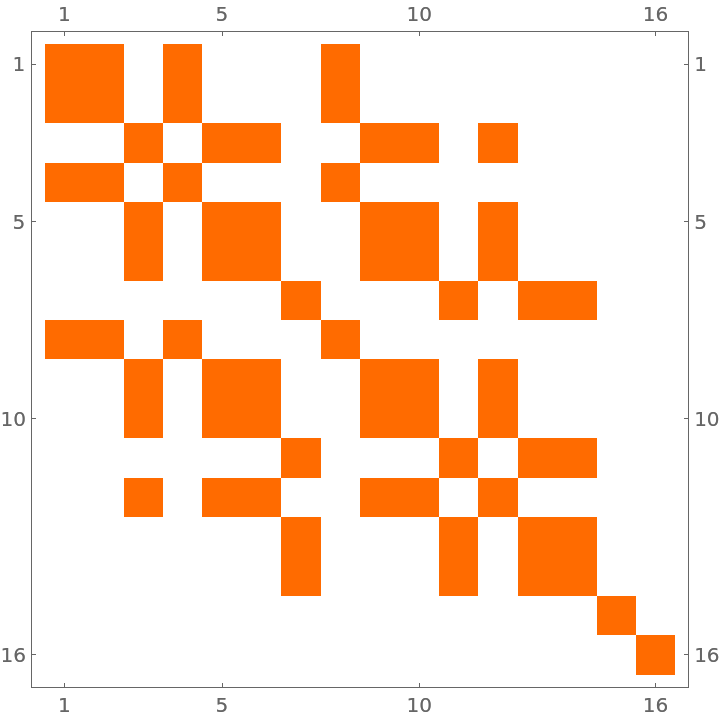
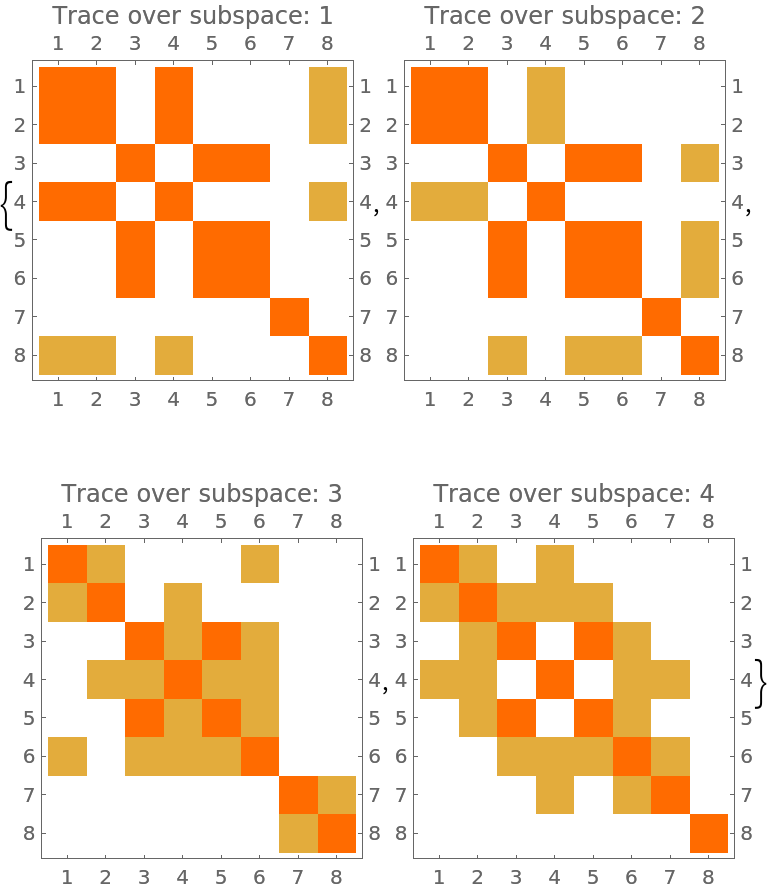
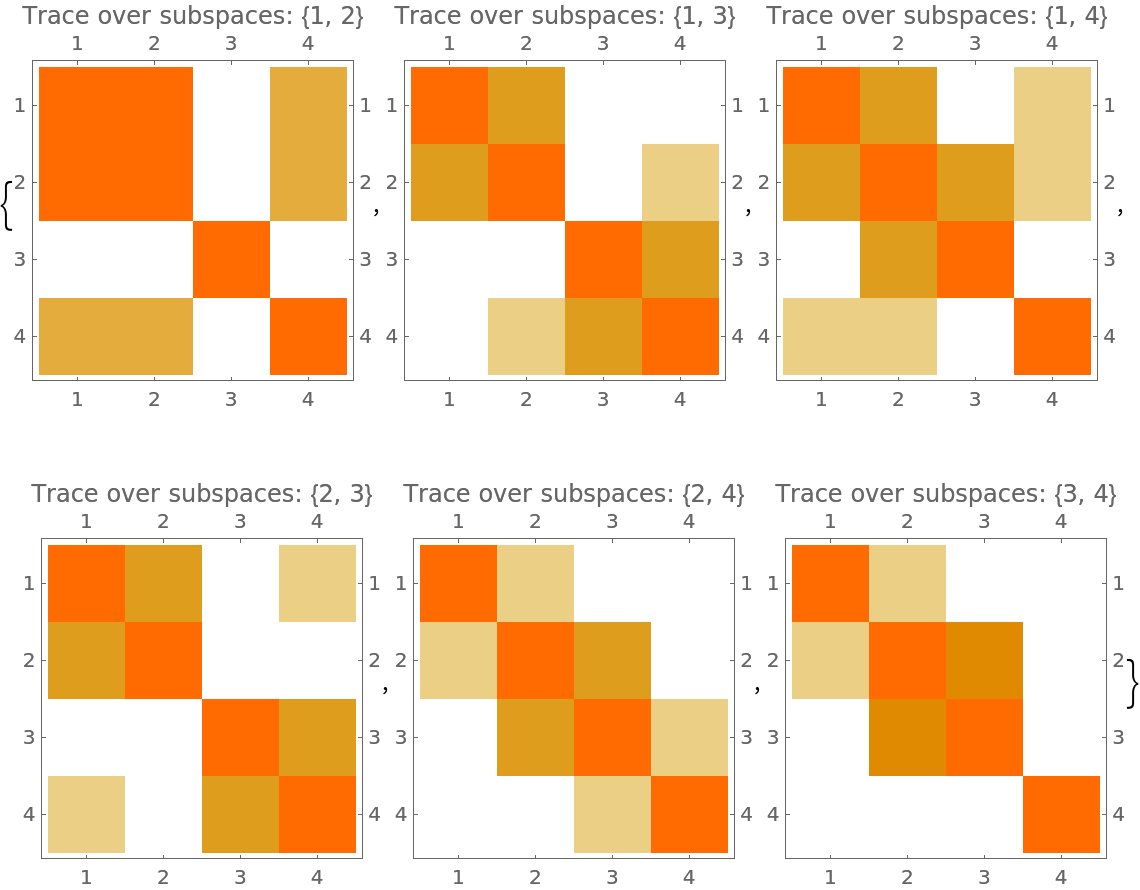
Plot the partial trace over an increasing number of subspaces:
![]() , i.e. of the tensor product of two subspaces
, i.e. of the tensor product of two subspaces ![]() :
:
![]() :
:





![mat = Array[Subscript[a, ##] &, {8, 8}];
rmat1 = ResourceFunction["MatrixPartialTrace"][mat, {1, 3}, {2, 2, 2}];
rmat2 = ResourceFunction["MatrixPartialTrace"][mat, {1, 3}, 2];](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/14d92ea0be141550.png)
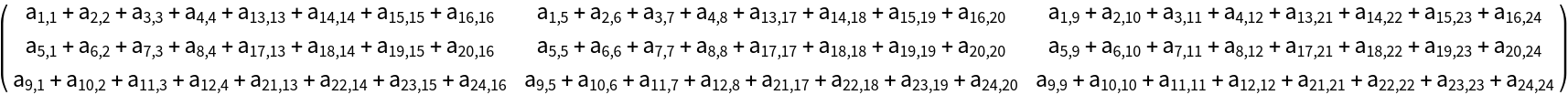



![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4413703f-d8a6-4492-b85b-5fd5be2b152f"]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/5b243fe398ab8366.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/05b121a7-fd50-4424-a57a-8ae8addf8fdf"]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/7d8361baeeabebaf.png)

![mat = RandomComplex[1 + I, {8, 8}];
mat = mat\[ConjugateTranspose] . mat;
Subscript[\[Rho], 123] = mat/Tr[mat];](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/0acd81e7d9a05504.png)
![mat = Array[a, {32, 32}];
rmat1 = ResourceFunction["MatrixPartialTrace"][mat, {1, 3, 5}, 2];
rmat2 = ResourceFunction["MatrixPartialTrace"][mat, {5, 3, 1}, 2];](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/427a3c475ebf41d0.png)
![rmat1 = ResourceFunction["MatrixPartialTrace"][mat, {3}, {2, 3, 2}];
rmat2 = ResourceFunction["MatrixPartialTrace"][rmat1, {2}, {2, 3}];
MatrixForm[rmat2]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/5f0ce0798a883c6b.png)
![rmat1 = ResourceFunction["MatrixPartialTrace"][mat, {1}, {2, 3, 2}];
rmat2 = ResourceFunction["MatrixPartialTrace"][rmat1, {1}, {3, 2}];
MatrixForm[rmat2]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/6435f1e83bb3fb45.png)
![rmat1 = ResourceFunction["MatrixPartialTrace"][mat, {2}, {2, 3, 2}];
rmat2 = ResourceFunction["MatrixPartialTrace"][rmat1, {1}, {2, 2}];
MatrixForm[rmat2]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/2790f456b340f26f.png)
![n = 4;
mat = Table[
Boole@PossibleZeroQ@
Total[IntegerDigits[i, 2, n] - IntegerDigits[j, 2, n]], {i, 2^
n}, {j, 2^n}];
MatrixPlot[mat]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/0c4e677f2043c3b4.png)
![MatrixPlot[ResourceFunction["MatrixPartialTrace"][mat, #, 2], PlotLabel -> ("Trace over subspace: " <> ToString[#])] & /@ Range[n]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/55021157959c324b.png)
![MatrixPlot[ResourceFunction["MatrixPartialTrace"][mat, #, 2], PlotLabel -> ("Trace over subspaces: " <> ToString[#])] & /@ Subsets[Range[n], {2}]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/4d6ee318ef02fba4.png)
![MatrixPlot[ResourceFunction["MatrixPartialTrace"][mat, #, 2], PlotLabel -> ("Trace over subspaces: " <> ToString[#])] & /@ Subsets[Range[n], {3}]](https://www.wolframcloud.com/obj/resourcesystem/images/b48/b4820fe9-025a-4c81-88db-5e15dc9cb00b/3f972b992d17294c.png)